In questa rubrica ci siamo occupati più volte di come la conoscenza scientifica si costruisca progressivamente attraverso gli esperimenti e le misure successive, gli errori e le replicazioni. Abbiamo anche parlato di alcuni effetti che possono distorcere questo processo: per esempio abbiamo descritto l’effetto sperimentatore, cioè l’involontaria (e inconsapevole) preferenza che un ricercatore ha per un particolare risultato della sua ricerca, per esempio perché conferma un risultato precedente:
Non c’è bisogno di imbrogliare o di sbagliarsi grossolanamente, può essere sufficiente controllare più accuratamente i risultati che ci paiono in contrasto con la nostra teoria per introdurre un subdolo artefatto nei dati. Per esempio, immaginate un esperimento di chimica in cui una reazione debba provocare un cambiamento di colore in una provetta. Facciamo l’esperimento dieci volte, cinque volte il cambiamento avviene e cinque no. Se la mia aspettativa è che la provetta cambi colore, sarò tentato di guardare due volte quelle in cui non cambia. Se, ricontrollandoli più attentamente, trovo tra questi due casi in cui la provetta era sporca, posso scartarli: ecco che il cambiamento di colore avviene cinque volte su otto e la mia teoria è confermata. Ma magari c’erano due casi da scartare anche tra i cinque in cui la reazione avveniva correttamente, e che non avevo ricontrollato perché mi sembravano “giusti”. (Da Query 4)
In questo numero ci occuperemo di una variante di questo effetto, sottile e a volte difficile da individuare ma interessante.
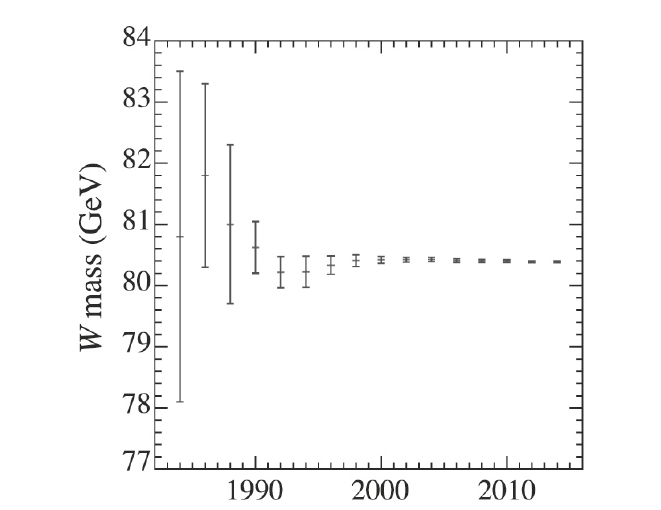
La velocità della luce è una quantità fondamentale in fisica, e una delle più misurate, anche perché il fatto che nel vuoto questa velocità sia costante è una nota conseguenze della teoria della relatività. La misura della velocità della luce con la massima precisione possibile può dunque servire a verificare sperimentalmente la validità della teoria, che sta alla base di gran parte della fisica moderna. In un articolo del 1985[1] Max Henrion e Baruch Fischhoff rappresentano su un grafico il valore misurato nei vari esperimenti in funzione dell’anno in cui il lavoro è stato pubblicato. Ogni punto corrisponde al valore misurato, e include una “barra di errore”, cioè un segmento che indica l’incertezza stimata sulla misura: più il segmento è corto, più la misura è precisa. Se il progressivo miglioramento delle tecniche di misura non avesse distorsioni, ci aspetteremmo che ogni nuova misura fosse vicina a quella precedente, con le barre di errore che si sovrappongono e progressivamente si accorciano, più o meno come succede nella figura 1 (che, per gli appassionati, si riferisce alla massa del bosone W[2]).
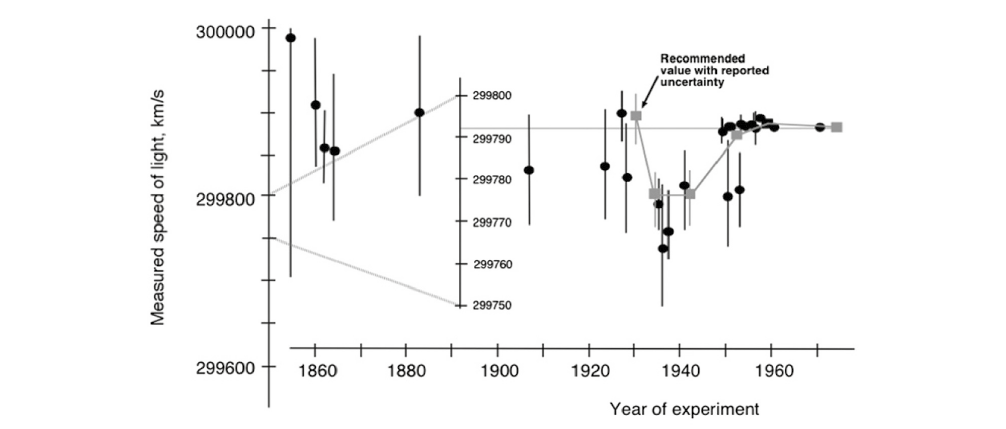
Quello che succede con la misura della velocità della luce è però diverso. Il grafico in fig. 2[3], che è un adattamento di quello originale, riporta come pallini neri i valori delle singole misure, e come quadratini più chiari un valore “raccomandato” stimato a partire da tutte le misure disponibili.
Nel 1929 il valore “raccomandato” rispecchia quello della misura più precisa fino ad allora disponibile. Nel 1933 il comitato che stabilisce la raccomandazione opta per un valore più basso, dando per qualche ragione più importanza alle tre misure intorno a 299780 km/s. Ed ecco che succede qualcosa di interessante: le successive quattro misure pubblicate sono molto più vicine al nuovo valore raccomandato che a quello precedente, o alla media dei due. Alla fine degli anni ’50 compaiono due nuove misure molto più precise, che spostano di nuovo il valore raccomandato vicino a quello del 1933; da allora in poi, le misure successive non si sposteranno di lì. Allan Franklin, in un classico articolo del 1983[4], lo ha chiamato bandwagon effect: in italiano si potrebbe dire “saltare sul carro del vincitore”. È possibile che, attraverso chissà quali minimi aggiustamenti come quelli descritti sopra, gli scienziati abbiano, inconsapevolmente, fatto in modo da avvicinare i loro risultati a quello che sembrava essere il valore al momento più plausibile per la quantità che stavano cercando di misurare. Certo, il caso della misura della velocità della luce potrebbe essere una coincidenza. Uno studio più recente[5], però, prendendo in considerazione l’evoluzione storica di molte misure di fisica delle particelle elementari, mostra come non solo la “barra di errore” sia spesso sottostimata, ma come le misure, osservate in funzione del tempo, tendano a raggrupparsi. Ossia, una volta individuato un “valore plausibile” di una certa quantità, le misure tendono a raggrupparsi intorno a quel valore.
Nella pratica questo effetto è interessante ma non troppo importante, per due ragioni. Da un lato, non è detto che il raggruppamento sia dovuto a processi “patologici” come l’effetto sperimentatore: si possono immaginare diversi meccanismi “legittimi” per spiegarlo. Per esempio, una sequenza di misure potrebbe basarsi su un’assunzione teorica o su un’altra misura che sarà poi a un certo punto corretta, provocando un salto nei valori misurati di lì in poi. In secondo luogo, l’effetto è piccolo, ed evidentemente si corregge un po’ alla volta col tempo. Tuttavia, non è completamente trascurabile: per giustificare il primo salto nel valore della velocità della luce ci fu chi ipotizzò che diminuisse col tempo; quando poi il valore misurato crebbe di nuovo, la dipendenza diventò un’oscillazione. Niente di grave, le ipotesi fanno parte del normale dibattito scientifico, ma comunque un piccolo spreco di energie per spiegare quello che con tutta probabilità è un artefatto dovuto ai complessi meccanismi che governano la costruzione del sapere scientifico.
Non c’è bisogno di imbrogliare o di sbagliarsi grossolanamente, può essere sufficiente controllare più accuratamente i risultati che ci paiono in contrasto con la nostra teoria per introdurre un subdolo artefatto nei dati. Per esempio, immaginate un esperimento di chimica in cui una reazione debba provocare un cambiamento di colore in una provetta. Facciamo l’esperimento dieci volte, cinque volte il cambiamento avviene e cinque no. Se la mia aspettativa è che la provetta cambi colore, sarò tentato di guardare due volte quelle in cui non cambia. Se, ricontrollandoli più attentamente, trovo tra questi due casi in cui la provetta era sporca, posso scartarli: ecco che il cambiamento di colore avviene cinque volte su otto e la mia teoria è confermata. Ma magari c’erano due casi da scartare anche tra i cinque in cui la reazione avveniva correttamente, e che non avevo ricontrollato perché mi sembravano “giusti”. (Da Query 4)
In questo numero ci occuperemo di una variante di questo effetto, sottile e a volte difficile da individuare ma interessante.
Figura 1 - Misure della massa del bosone W
Quello che succede con la misura della velocità della luce è però diverso. Il grafico in fig. 2[3], che è un adattamento di quello originale, riporta come pallini neri i valori delle singole misure, e come quadratini più chiari un valore “raccomandato” stimato a partire da tutte le misure disponibili.
Figura 2 - Misure della velocità della luce in diversi decenni
Nella pratica questo effetto è interessante ma non troppo importante, per due ragioni. Da un lato, non è detto che il raggruppamento sia dovuto a processi “patologici” come l’effetto sperimentatore: si possono immaginare diversi meccanismi “legittimi” per spiegarlo. Per esempio, una sequenza di misure potrebbe basarsi su un’assunzione teorica o su un’altra misura che sarà poi a un certo punto corretta, provocando un salto nei valori misurati di lì in poi. In secondo luogo, l’effetto è piccolo, ed evidentemente si corregge un po’ alla volta col tempo. Tuttavia, non è completamente trascurabile: per giustificare il primo salto nel valore della velocità della luce ci fu chi ipotizzò che diminuisse col tempo; quando poi il valore misurato crebbe di nuovo, la dipendenza diventò un’oscillazione. Niente di grave, le ipotesi fanno parte del normale dibattito scientifico, ma comunque un piccolo spreco di energie per spiegare quello che con tutta probabilità è un artefatto dovuto ai complessi meccanismi che governano la costruzione del sapere scientifico.
Note
1) M. Henrion, B. Fischhoff, “Assessing uncertainty in physical constants”, Am. J. Phys. 54(9):791-798 (1985)
2) C. Patrignani et al. (Particle Data Group), “Review of Particle Properties (2016)” Chin. Phys. C 40:100001 (2016)
3) M. Granger Morgan. “Use (and abuse) of expert elicitation in support of decision making for public policy” PNAS 111(20):7176-7184 (2014)
4) A. Franklin, “Forging cooking, trimming and riding on the bandwagon” Am. J. Phys. 52(9):786-793 (1983)
5) M. Jeng, “Bandwagon effects and error bars in particle physics” Nucl. Instr. Meth. A571:704-708 (2007)
