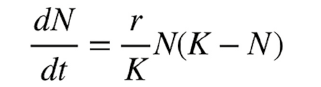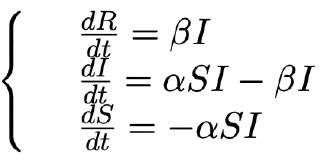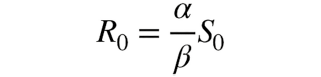[1]
Come si diffonde un’epidemia? Che tipo di andamento è possibile aspettarsi nel tempo? Come si diffonde geograficamente? È possibile fare delle previsioni a partire dai dati di cui si dispone?
Queste domande, e più in generale il tema delle epidemie, sono diventate di grande attualità quando dalla seconda metà di gennaio in Cina si è iniziato a parlare della diffusione del Coronavirus COVID-19. Quando poi, a partire da fine febbraio, anche in Italia ci sono stati i primi focolai di infezione questo è purtroppo diventato uno degli argomenti più discussi sui media e nelle case degli italiani.
La risposta alle domande iniziali non è banale e certamente non può essere contenuta in questo articolo.
Se però un messaggio deve passare, è che ci sono strumenti per studiare la diffusione del contagio e questi strumenti di tipo statistico matematico si affiancano a quelli usati in campo medico e biologico.
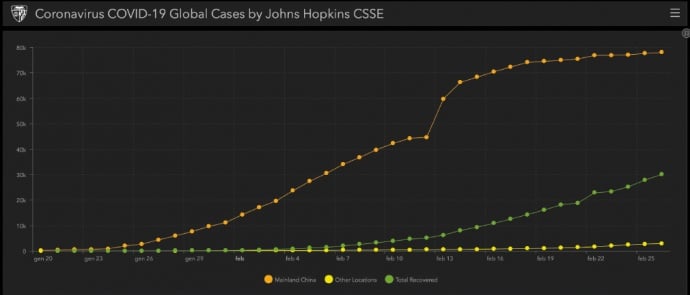
Un primo passo per visualizzare l’evoluzione di un’epidemia è riportare i dati su un grafico. Probabilmente molti dei lettori avranno visitato il sito web realizzato dalla Johns Hopkins University.
Anche se osservando il grafico si possono già dedurre delle informazioni (per esempio quanto cresce l’epidemia, se si è arrivati in una zona di plateau in cui ha smesso di crescere), la matematica può fare molto di più: può creare dei modelli.
Storicamente, il primo modello di tipo matematico in ambito epidemiologico fu formulato, nel 1760, da Daniel Bernoulli nel tentativo di supportare la vaccinazione contro il vaiolo.
Uno dei più semplici modelli che si possono utilizzare per descrivere l’evoluzione di un’epidemia è la curva logistica, nota anche come modello Verhulst, poiché venne sviluppata dal matematico e statistico belga Pierre François Verhulst.
In comune a tutti i modelli che vedremo c’è il fatto che possono essere usati per provare a spiegare il comportamento di fenomeni molto diversi tra loro. In fondo, come diceva Poincaré, «la matematica è l’arte di dare lo stesso nome a cose diverse»[2].
Il modello logistico studia la variazione degli individui in funzione del numero N di quelli presenti al tempo t.
Il modello può essere descritto da questa relazione:
N rappresenta il numero di individui in funzione del tempo che passa, r il loro tasso di crescita (più è alto r, più velocemente aumenteranno) e K il numero di individui nello stato di equilibrio, dN/dt è la derivata di N, ossia la variazione della popolazione nel tempo.
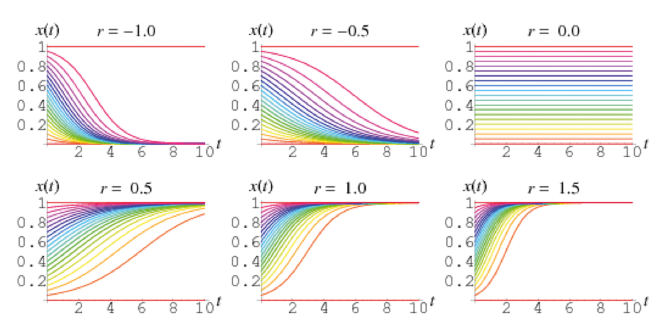
L’andamento che si ottiene è una curva, che al variare dei parametri può assumere un andamento simile a quello mostrato nella figura 2.
La curva rappresentata in figura 2 assume per alcuni valori di r un andamento simile ad una “s” un po’ schiacciata. In un primo tratto quindi la popolazione (nel nostro caso l’epidemia) cresce in modo molto rapido (andamento analogo a quello di una esponenziale), per poi stabilizzarsi e tendere verso un andamento orizzontale di equilibrio.
Ovviamente questo modello ha dei limiti, legati alla sua semplicità. Si può fare qualcosa di più “sofisticato”, ad esempio nel modello SIR.
 [3]
[3]
Gli scienziati Kermack e McKendrick proposero un modello di tipo differenziale per spiegare la rapida crescita e successiva decrescita del numero di persone infette osservate in alcune epidemie, come la peste (Londra 1665-1666, Bombay 1906) e il colera (Londra 1865). Questo modello è indicato con l’acronimo SIR perché suddivide la popolazione in tre classi, S, I e R così definite:
Ovviamente, se indichiamo con N la popolazione totale dovremo avere che questo termine corrisponda alla somma delle tre classi:
S + I + R = N
Il modello SIR inoltre aggiunge le seguenti ipotesi (non del tutto realistiche, ma un modello è sempre necessariamente falso in quanto semplificazione della realtà):
L’idea può essere schematizzata in questo modo: S → I → R:
un individuo da sano diventa infetto, e da questo stato passa a quello di rimosso (perché immunizzato, deceduto o isolato).
Il modello può essere scritto con il seguente sistema di equazioni differenziali (ovvero equazioni che uniscono una grandezza e la sua variazione nel tempo).
In questo sistema, I, R e S come detto sono la popolazione di infetti, rimossi e suscettibili, mentre α e β sono parametri positivi. Al tempo “zero”, si assume che siano presenti un certo numero di suscettibili e infetti (o l’infezione non può diffondersi), e nessun rimosso.
Senza entrare nel dettaglio, l’idea è che, in base alle assunzioni del modello, il numero di nuovi contagiati e quello di nuovi infetti è proporzionale al numero di contatti tra individui nella classe S e individui nella classe I. Inoltre, gli individui malati guariscono proporzionalmente al numero dei malati.
Nel caso in cui non siano disponibili cure e non si abbia ancora un vaccino (come per il Coronavirus COVID-19), una strategia utile è aumentare il numero di rimossi (mettendo in isolamento le persone contagiate in attesa della loro guarigione).
Lo studio del sistema di equazioni precedentemente scritto, ci fornisce delle indicazioni chiare riguardo ciò, legate ai valori di α e β.. In particolare, si può definire un parametro, il tasso di riproduttività di base, R0, così definito:
Se R0 >1, l’epidemia si propaga; se, invece, R0 <1, si estingue. Questo parametro può esser letto come il “numero medio di persone che il singolo infetto può contagiare prima di guarire” e si può ridurre “rendendo difficile la vita” al virus: da qui le politiche di “quarantena” dell’ultimo periodo.
Quelli fin qui descritti sono solo due fra i più semplici modelli sviluppati. Ne esistono svariati altri che tengono conto della posizione geografica, del tipo di malattia, e di una serie di altri fattori che servono a rendere un modello più simile al fenomeno studiato.
Questi modelli, applicati ai dati sulle passate epidemie , hanno dimostrato di riuscire in buona approssimazione a descrivere l’andamento di questi fenomeni.
A questo punto crediamo sia chiaro al lettore quanto ci sia bisogno di modelli sempre più sviluppati in grado di fare previsioni precise.
Ancora una volta, c’è bisogno di tanta scienza.
Nei momenti di grande difficoltà, quando sembra che sia la paura a farla da padrone, non c’è che un unico antidoto: affidarsi alla scienza che, con tutti i suoi limiti, è l’unica arma per le difficoltà di oggi e per quelle del futuro.
Come si diffonde un’epidemia? Che tipo di andamento è possibile aspettarsi nel tempo? Come si diffonde geograficamente? È possibile fare delle previsioni a partire dai dati di cui si dispone?
Queste domande, e più in generale il tema delle epidemie, sono diventate di grande attualità quando dalla seconda metà di gennaio in Cina si è iniziato a parlare della diffusione del Coronavirus COVID-19. Quando poi, a partire da fine febbraio, anche in Italia ci sono stati i primi focolai di infezione questo è purtroppo diventato uno degli argomenti più discussi sui media e nelle case degli italiani.
La risposta alle domande iniziali non è banale e certamente non può essere contenuta in questo articolo.
Se però un messaggio deve passare, è che ci sono strumenti per studiare la diffusione del contagio e questi strumenti di tipo statistico matematico si affiancano a quelli usati in campo medico e biologico.
Un primo passo per visualizzare l’evoluzione di un’epidemia è riportare i dati su un grafico. Probabilmente molti dei lettori avranno visitato il sito web realizzato dalla Johns Hopkins University.
Anche se osservando il grafico si possono già dedurre delle informazioni (per esempio quanto cresce l’epidemia, se si è arrivati in una zona di plateau in cui ha smesso di crescere), la matematica può fare molto di più: può creare dei modelli.
Storicamente, il primo modello di tipo matematico in ambito epidemiologico fu formulato, nel 1760, da Daniel Bernoulli nel tentativo di supportare la vaccinazione contro il vaiolo.
Uno dei più semplici modelli che si possono utilizzare per descrivere l’evoluzione di un’epidemia è la curva logistica, nota anche come modello Verhulst, poiché venne sviluppata dal matematico e statistico belga Pierre François Verhulst.
In comune a tutti i modelli che vedremo c’è il fatto che possono essere usati per provare a spiegare il comportamento di fenomeni molto diversi tra loro. In fondo, come diceva Poincaré, «la matematica è l’arte di dare lo stesso nome a cose diverse»[2].
Il modello Verhulst
Il modello logistico studia la variazione degli individui in funzione del numero N di quelli presenti al tempo t.
Il modello può essere descritto da questa relazione:
N rappresenta il numero di individui in funzione del tempo che passa, r il loro tasso di crescita (più è alto r, più velocemente aumenteranno) e K il numero di individui nello stato di equilibrio, dN/dt è la derivata di N, ossia la variazione della popolazione nel tempo.
L’andamento che si ottiene è una curva, che al variare dei parametri può assumere un andamento simile a quello mostrato nella figura 2.
La curva rappresentata in figura 2 assume per alcuni valori di r un andamento simile ad una “s” un po’ schiacciata. In un primo tratto quindi la popolazione (nel nostro caso l’epidemia) cresce in modo molto rapido (andamento analogo a quello di una esponenziale), per poi stabilizzarsi e tendere verso un andamento orizzontale di equilibrio.
Ovviamente questo modello ha dei limiti, legati alla sua semplicità. Si può fare qualcosa di più “sofisticato”, ad esempio nel modello SIR.

Figura 2: esempio di andamento della curva logistica al variare del parametro r. In questo caso si è indicato con x(t) il rapporto fra N(t) e K
Il modello SIR
Gli scienziati Kermack e McKendrick proposero un modello di tipo differenziale per spiegare la rapida crescita e successiva decrescita del numero di persone infette osservate in alcune epidemie, come la peste (Londra 1665-1666, Bombay 1906) e il colera (Londra 1865). Questo modello è indicato con l’acronimo SIR perché suddivide la popolazione in tre classi, S, I e R così definite:
- gli individui sani sono indicati con il termine S ovvero Suscettibili, che possono essere contagiati;
- i malati sono indicati con I, cioè Infetti, e hanno la caratteristica di poter trasmettere l’infezione;
- i guariti (o deceduti) sono indicati con R, che sta per Rimossi poiché immunizzati e non più in grado di essere contagiati o contagiare.
Ovviamente, se indichiamo con N la popolazione totale dovremo avere che questo termine corrisponda alla somma delle tre classi:
S + I + R = N
Il modello SIR inoltre aggiunge le seguenti ipotesi (non del tutto realistiche, ma un modello è sempre necessariamente falso in quanto semplificazione della realtà):
- 1. un infetto è immediatamente infettivo, ovvero non c’è tempo di incubazione;
- 2. il contagio avviene per contatto diretto;
- 3. la probabilità di incontro tra due qualsiasi individui della popolazione è la stessa;
- 4. ogni individuo malato ha probabilità di guarigione per unità di tempo costante.
L’idea può essere schematizzata in questo modo: S → I → R:
un individuo da sano diventa infetto, e da questo stato passa a quello di rimosso (perché immunizzato, deceduto o isolato).
Il modello può essere scritto con il seguente sistema di equazioni differenziali (ovvero equazioni che uniscono una grandezza e la sua variazione nel tempo).
In questo sistema, I, R e S come detto sono la popolazione di infetti, rimossi e suscettibili, mentre α e β sono parametri positivi. Al tempo “zero”, si assume che siano presenti un certo numero di suscettibili e infetti (o l’infezione non può diffondersi), e nessun rimosso.
Senza entrare nel dettaglio, l’idea è che, in base alle assunzioni del modello, il numero di nuovi contagiati e quello di nuovi infetti è proporzionale al numero di contatti tra individui nella classe S e individui nella classe I. Inoltre, gli individui malati guariscono proporzionalmente al numero dei malati.
Nel caso in cui non siano disponibili cure e non si abbia ancora un vaccino (come per il Coronavirus COVID-19), una strategia utile è aumentare il numero di rimossi (mettendo in isolamento le persone contagiate in attesa della loro guarigione).
Lo studio del sistema di equazioni precedentemente scritto, ci fornisce delle indicazioni chiare riguardo ciò, legate ai valori di α e β.. In particolare, si può definire un parametro, il tasso di riproduttività di base, R0, così definito:
Se R0 >1, l’epidemia si propaga; se, invece, R0 <1, si estingue. Questo parametro può esser letto come il “numero medio di persone che il singolo infetto può contagiare prima di guarire” e si può ridurre “rendendo difficile la vita” al virus: da qui le politiche di “quarantena” dell’ultimo periodo.
Brevi e parziali conclusioni
Quelli fin qui descritti sono solo due fra i più semplici modelli sviluppati. Ne esistono svariati altri che tengono conto della posizione geografica, del tipo di malattia, e di una serie di altri fattori che servono a rendere un modello più simile al fenomeno studiato.
Questi modelli, applicati ai dati sulle passate epidemie , hanno dimostrato di riuscire in buona approssimazione a descrivere l’andamento di questi fenomeni.
A questo punto crediamo sia chiaro al lettore quanto ci sia bisogno di modelli sempre più sviluppati in grado di fare previsioni precise.
Ancora una volta, c’è bisogno di tanta scienza.
Nei momenti di grande difficoltà, quando sembra che sia la paura a farla da padrone, non c’è che un unico antidoto: affidarsi alla scienza che, con tutti i suoi limiti, è l’unica arma per le difficoltà di oggi e per quelle del futuro.
Note
2) H. Poincaré, “Science et méthode”, Paris 1908, p. 29.
Bibliografia
- Bernoulli D., An attempt at a new analysis of the mortality caused by smallpox and of the advantages of inoculation to prevent it, reviewed by S. Blower, Rev. Med. Virol. 14 (2004) 275–288.
- W. O. Kermack, A. G. McKendrick: A Contribution to the Mathematical Theory of Epidemics, Proc. Royal Soc. London. Ser. A, Vol. 115, Issue 772 (1927), 700-721.
- C. Mascia, E. Montefusco, Dispense del Corso di Modelli Analitici per le Applicazioni: Modelli deterministici in epidemiologia, disponibili al seguente link: https://bit.ly/2IFr3xz