Con tutta probabilità, quando nel 1949 Arthur Miller scrisse Morte di un commesso viaggiatore, la sua più opera più celebre, non sapeva che l'idea di usare un "commesso viaggiatore" per descrivere un problema era in realtà venuta anche ai matematici.
Julia Robinson, proprio nello stesso anno, scrisse un report per la Rand Corporation in cui utilizzava la terminologia "Traveling Salesman Problem" (TSP) per indicare un dilemma che dal punto di vista matematico ha una storia più antica.
Mentre Morte di un commesso viaggiatore è un'opera teatrale fra le più amate del '900 in cui si affronta la crisi del sogno americano, il "problema del commesso viaggiatore" cerca di trovare il cammino più breve che un viaggiatore deve percorrere per visitare tutte le città in una regione. Quindi le similitudini probabilmente sono limitate al nome, però la coincidenza del 1949 è davvero curiosa.
La storia "matematica" del commesso viaggiatore è un po' oscura e molto lunga. Un tentativo di ricostruzione viene fatto da Gilbert Laporte (in bibliografia): questi divide il problema nell'era pre computer e quella del computer, scegliendo come data spartiacque il 1950 (anno successivo a quello del report di Robinson e dell'opera di Miller).
Già nel 1759 il grande matematico Eulero aveva affrontato quello che aveva chiamato "il problema dei cavalieri"; nel 1800 William Rowan Hamilton si occupò di un problema similare inventando anche un gioco matematico noto come puzzle di Hamilton (o Icosian game), che consisteva nel trovare un cammino chiuso sul bordo di un dodecaedro.
Probabilmente la primissima volta che il problema venne formulato con il nome attuale fu in un manuale non di matematica, scritto in tedesco e destinato proprio a ... commessi viaggiatori. Il titolo potrebbe essere tradotto così: "Il commesso viaggiatore – come dovrebbe essere e cosa dovrebbe fare, per ricevere gli ordini e assicurare il successo alla sua attività – da un vecchio commesso viaggiatore".
Un approccio ingenuo potrebbe far pensare che, in fondo, dato che questa tipologia di lavoro esiste da tempo (oggi nelle sue versioni più moderne figlie dell'e-commerce), il problema non sia così complicato, altrimenti non si spiegherebbe come sia stato possibile per questi poveri commessi continuare a lavorare in tutti questi secoli.
Se ci si sofferma con più attenzione si nota, però, che è meno semplice di quel che sembra: l'obiettivo è quello di viaggiare sul percorso più breve possibile partendo e tornando dalla propria casa, visitando una sola volta ognuna delle diverse città. Se il numero di città da visitare diventa molto grande cominciano i guai. Per trovare il percorso ottimale tutti gli algoritmi conosciuti sono di complessità esponenziale! Ovvero? All'aumentare del numero di luoghi da visitare, il tempo che servirebbe alla risoluzione diventa enorme, non c'è computer che tenga!
Ma, in fondo, è davvero un problema così importante? I commessi viaggiatori saranno pure sfortunati, ma in fondo sono fatti loro, giusto? Falso! Come quasi sempre in matematica, si scopre che gli sforzi fatti per risolvere un problema di un tipo sono generalizzabili e si applicano a innumerevoli situazioni differenti: per esempio, se si deve progettare una successione di azioni da compiere o si devono allocare risorse, si scopre che il problema da risolvere è lo stesso di Arthur Miller. Il TSP è un problema non banale dell'umanità.
Il TSP fa parte di un'intera tipologia di problemi chiamati NP-completi. Sono problemi che, per adesso, sono risolti solo da algoritmi di complessità esponenziale. Sono tutti legati tra loro, e se si trovasse un algoritmo di complessità polinomiale per uno, questo si rifletterebbe sulla soluzione di ogni altro. Non è una cosa di poca rilevanza. A conferma di ciò, "P vs NP" rientra nei cosiddetti Problemi del Millennio e il Clay Institute ha messo in palio un premio da un milione di dollari per chiunque lo risolverà. Se qualcuno inventasse un algoritmo di complessità polinomiale per risolvere il problema del commesso viaggiatore (ma anche quello della ricerca di un ciclo hamiltoniano) intascherebbe una bella somma.
Attualmente ci sono diverse strategie per i problemi NP-completi, come:
Mostriamo in pratica come approcciare il problema del TSP (consigliamo la lettura dell'articolo del numero precedente , che tratta di tematiche simili sotto un diverso punto di vista) partendo da un caso semplice, formato da quattro città:
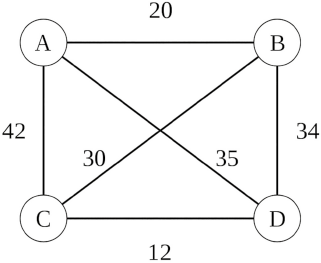
A è la città che contiene il centro di smistamento da cui parte e torna il commesso viaggiatore. Il disegno non rappresenta fedelmente la mappa della regione geografica, ma condensa le informazioni essenziali al problema in un grafo pesato. Siamo abituati a questo tipo di sintesi che si opera nella quotidianità per altri modelli, come le mappe di un navigatore o la pianta della metro di una città, e che è il tipo di approccio alla modellistica matematica in generale.
L'idea più basilare, quella di ricerca esaustiva, consiste nel provare tutte le opzioni disponibili, per poi scegliere la migliore. Dato che il commesso parte da A, la città successiva da visitare può essere B, C o D, e una volta scelta la seconda, per la terza ha due opzioni, l'ultima è determinata univocamente. In totale ci sono quindi sei differenti strade:
Per essere precisi, le differenti strade sono solo le prime tre, le altre sono le stesse percorse a ritroso. Facendo il calcolo delle lunghezze, il percorso ottimale è quello A->B->C->D->A, di 97 km.
Il motivo per cui questo approccio non può funzionare in generale è la velocità con cui il problema diventa ingestibile all'aumentare del numero di città: quando le città sono una cinquantina, il numero di percorsi è nell'ordine di 10^63, ovvero dei miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi. Se anche fosse possibile (e non lo è) non avrebbe senso utilizzare tanta potenza di calcolo per un algoritmo così ingenuo.
Cambiamo quindi punto di vista, scegliendo un algoritmo euristico, per la precisione un algoritmo genetico, figlio di un'idea scaturita inizialmente tra gli anni '50 e '60. Se l'Evoluzione biologica ha portato gli organismi viventi a questo livello di complessità e specializzazione, perché non sfruttare lo stesso meccanismo per risolvere problemi di natura ingegneristica, informatica o combinatoria?
Nel 1975 John Holland (vedi bibliografia) presentò l'algoritmo genetico come astrazione dell'evoluzione biologica e diede un inquadramento teorico a adattamento e selezione. Ecco l'idea, direttamente applicata al TSP.
All'inizio è presente un insieme di percorsi differenti, ad esempio selezionati casualmente, tutti che partono e finiscono in A, e tutti differenti tra loro. Questa è la popolazione iniziale e ogni percorso è un individuo. Gli individui sono sottoposti a una pressione selettiva data dal problema: i più adatti sono ovviamente quelli di meno chilometri, ed è possibile ordinare quindi i risultati dal più al meno buono.
Solamente i più adatti sopravvivono: i percorsi peggiori vengono eliminati e la generazione successiva è formata dai figli dei primi classificati, ottenuti tramite incroci e mutazioni. Ad esempio, si può pensare di generare un nuovo individuo facendo un mix tra due precedenti (crossing over) oppure modificando casualmente alcune delle tappe, facendo passare il commesso prima in una città piuttosto che in un'altra (mutazioni).
Ottenuta la nuova generazione il ciclo si ripete:
Si può mostrare come con il passare del tempo si producano individui sempre più performanti, avvicinandosi al risultato ottimale. Da sottolineare come non sia garantito che il risultato ottimale venga raggiunto, almeno non in tempi brevi: in un algoritmo euristico si decide di far evolvere il sistema solo finché il risultato non sia abbastanza buono da accontentare le esigenze. Vogliamo una soluzione in tempi brevi, quindi accontentiamoci pure di un risultato sub-ottimale.
Julia Robinson, proprio nello stesso anno, scrisse un report per la Rand Corporation in cui utilizzava la terminologia "Traveling Salesman Problem" (TSP) per indicare un dilemma che dal punto di vista matematico ha una storia più antica.
Mentre Morte di un commesso viaggiatore è un'opera teatrale fra le più amate del '900 in cui si affronta la crisi del sogno americano, il "problema del commesso viaggiatore" cerca di trovare il cammino più breve che un viaggiatore deve percorrere per visitare tutte le città in una regione. Quindi le similitudini probabilmente sono limitate al nome, però la coincidenza del 1949 è davvero curiosa.
La storia "matematica" del commesso viaggiatore è un po' oscura e molto lunga. Un tentativo di ricostruzione viene fatto da Gilbert Laporte (in bibliografia): questi divide il problema nell'era pre computer e quella del computer, scegliendo come data spartiacque il 1950 (anno successivo a quello del report di Robinson e dell'opera di Miller).
Già nel 1759 il grande matematico Eulero aveva affrontato quello che aveva chiamato "il problema dei cavalieri"; nel 1800 William Rowan Hamilton si occupò di un problema similare inventando anche un gioco matematico noto come puzzle di Hamilton (o Icosian game), che consisteva nel trovare un cammino chiuso sul bordo di un dodecaedro.
Probabilmente la primissima volta che il problema venne formulato con il nome attuale fu in un manuale non di matematica, scritto in tedesco e destinato proprio a ... commessi viaggiatori. Il titolo potrebbe essere tradotto così: "Il commesso viaggiatore – come dovrebbe essere e cosa dovrebbe fare, per ricevere gli ordini e assicurare il successo alla sua attività – da un vecchio commesso viaggiatore".
Un approccio ingenuo potrebbe far pensare che, in fondo, dato che questa tipologia di lavoro esiste da tempo (oggi nelle sue versioni più moderne figlie dell'e-commerce), il problema non sia così complicato, altrimenti non si spiegherebbe come sia stato possibile per questi poveri commessi continuare a lavorare in tutti questi secoli.
Se ci si sofferma con più attenzione si nota, però, che è meno semplice di quel che sembra: l'obiettivo è quello di viaggiare sul percorso più breve possibile partendo e tornando dalla propria casa, visitando una sola volta ognuna delle diverse città. Se il numero di città da visitare diventa molto grande cominciano i guai. Per trovare il percorso ottimale tutti gli algoritmi conosciuti sono di complessità esponenziale! Ovvero? All'aumentare del numero di luoghi da visitare, il tempo che servirebbe alla risoluzione diventa enorme, non c'è computer che tenga!
Ma, in fondo, è davvero un problema così importante? I commessi viaggiatori saranno pure sfortunati, ma in fondo sono fatti loro, giusto? Falso! Come quasi sempre in matematica, si scopre che gli sforzi fatti per risolvere un problema di un tipo sono generalizzabili e si applicano a innumerevoli situazioni differenti: per esempio, se si deve progettare una successione di azioni da compiere o si devono allocare risorse, si scopre che il problema da risolvere è lo stesso di Arthur Miller. Il TSP è un problema non banale dell'umanità.
Il TSP fa parte di un'intera tipologia di problemi chiamati NP-completi. Sono problemi che, per adesso, sono risolti solo da algoritmi di complessità esponenziale. Sono tutti legati tra loro, e se si trovasse un algoritmo di complessità polinomiale per uno, questo si rifletterebbe sulla soluzione di ogni altro. Non è una cosa di poca rilevanza. A conferma di ciò, "P vs NP" rientra nei cosiddetti Problemi del Millennio e il Clay Institute ha messo in palio un premio da un milione di dollari per chiunque lo risolverà. Se qualcuno inventasse un algoritmo di complessità polinomiale per risolvere il problema del commesso viaggiatore (ma anche quello della ricerca di un ciclo hamiltoniano) intascherebbe una bella somma.
Attualmente ci sono diverse strategie per i problemi NP-completi, come:
- trovare un caso specifico del problema (sottoproblema) per il quale sia possibile una soluzione esatta;
- progettare algoritmi euristici, cioè algoritmi che producono soluzioni probabilmente buone, ma non necessariamente ottimali;
- progettare algoritmi per trovare la soluzione esatta, ragionevolmente veloci solo per problemi con un numero di input relativamente basso (un basso numero di città, nel caso del TSP).
Mostriamo in pratica come approcciare il problema del TSP (consigliamo la lettura dell'articolo del numero precedente , che tratta di tematiche simili sotto un diverso punto di vista) partendo da un caso semplice, formato da quattro città:
L'idea più basilare, quella di ricerca esaustiva, consiste nel provare tutte le opzioni disponibili, per poi scegliere la migliore. Dato che il commesso parte da A, la città successiva da visitare può essere B, C o D, e una volta scelta la seconda, per la terza ha due opzioni, l'ultima è determinata univocamente. In totale ci sono quindi sei differenti strade:
- A->B->C->D->A
- A->B->D->C->A
- A->C->D->B->A
- A->C->B->D->A
- A->D->B->C->A
- A->D->C->B->A
Per essere precisi, le differenti strade sono solo le prime tre, le altre sono le stesse percorse a ritroso. Facendo il calcolo delle lunghezze, il percorso ottimale è quello A->B->C->D->A, di 97 km.
Il motivo per cui questo approccio non può funzionare in generale è la velocità con cui il problema diventa ingestibile all'aumentare del numero di città: quando le città sono una cinquantina, il numero di percorsi è nell'ordine di 10^63, ovvero dei miliardi di miliardi di miliardi di miliardi di miliardi di miliardi di miliardi. Se anche fosse possibile (e non lo è) non avrebbe senso utilizzare tanta potenza di calcolo per un algoritmo così ingenuo.
Cambiamo quindi punto di vista, scegliendo un algoritmo euristico, per la precisione un algoritmo genetico, figlio di un'idea scaturita inizialmente tra gli anni '50 e '60. Se l'Evoluzione biologica ha portato gli organismi viventi a questo livello di complessità e specializzazione, perché non sfruttare lo stesso meccanismo per risolvere problemi di natura ingegneristica, informatica o combinatoria?
Nel 1975 John Holland (vedi bibliografia) presentò l'algoritmo genetico come astrazione dell'evoluzione biologica e diede un inquadramento teorico a adattamento e selezione. Ecco l'idea, direttamente applicata al TSP.
All'inizio è presente un insieme di percorsi differenti, ad esempio selezionati casualmente, tutti che partono e finiscono in A, e tutti differenti tra loro. Questa è la popolazione iniziale e ogni percorso è un individuo. Gli individui sono sottoposti a una pressione selettiva data dal problema: i più adatti sono ovviamente quelli di meno chilometri, ed è possibile ordinare quindi i risultati dal più al meno buono.
Solamente i più adatti sopravvivono: i percorsi peggiori vengono eliminati e la generazione successiva è formata dai figli dei primi classificati, ottenuti tramite incroci e mutazioni. Ad esempio, si può pensare di generare un nuovo individuo facendo un mix tra due precedenti (crossing over) oppure modificando casualmente alcune delle tappe, facendo passare il commesso prima in una città piuttosto che in un'altra (mutazioni).
Ottenuta la nuova generazione il ciclo si ripete:
- selezione degli individui-percorsi più adatti con eliminazione dei meno performanti;
- incrocio e mutazioni tra i restanti;
- creazione della nuova generazione.
Si può mostrare come con il passare del tempo si producano individui sempre più performanti, avvicinandosi al risultato ottimale. Da sottolineare come non sia garantito che il risultato ottimale venga raggiunto, almeno non in tempi brevi: in un algoritmo euristico si decide di far evolvere il sistema solo finché il risultato non sia abbastanza buono da accontentare le esigenze. Vogliamo una soluzione in tempi brevi, quindi accontentiamoci pure di un risultato sub-ottimale.
Riferimenti bibliografici
- J. Robinson, On the Hamiltonian Game (A Traveling Salesman Problem), Research Memorandum RM-303, The RAND Corporation, Santa Monica, California, (5 December) 1949.
- G. Laporte, A Short History of the Traveling Salesman problem, disponibile al seguente link: https://bit.ly/3HXtAj7 .
- Solution d'une question curieuse qui ne paraît soumise à aucune analyse, Mémoires de l'Académie Royale des Sciences et Belles Lettres, Année 1759, vol.15, pp.310-337, Berlin (1766).
- M. Fortin, LP-based Heuristics for the Traveling Salesman Problem, tesi di Dottorato di Ricerca in Automatica e Ricerca Operativa, disponibile qui: https://bit.ly/33caTtg .
- J.H. Holland. Adaptation in Natural and Artificial Systems. University of Michigan Press, 1975.
