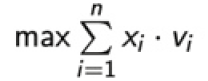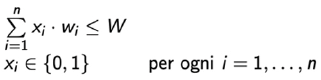Non so se è capitato anche a voi lettori, ma a noi, all’epoca del liceo, più o meno quotidianamente si poneva il problema del far entrare tutti i libri nello zaino; ammirando quei compagni di classe che riuscivano a portare solo un foglio e una penna, noi da eterni insicuri caricavamo lo zaino di libri e quaderni per ogni materia. Quando poi c’era la versione di latino o il compito di inglese, far entrare anche il vocabolario diventava un’impresa.
Perlomeno, oggi possiamo vantarci del fatto che stavamo affrontando un noto problema di ottimizzazione matematica, chiamato appunto “problema dello zaino” (“Knapsack problem”, lo abbiamo già citato nel precedente articolo della rubrica dal titolo “Ottimizzazione, pensiero razionale...e formiche”).
Come sempre capita in matematica, la classe di problemi di cui parliamo è generale e non si riduce a preparare uno zaino o una valigia, esempi che fungono solo da modelli chiarificatori. Gestire le scorte di un magazzino, investire in pacchetti azionari, trovare la maniera meno dispendiosa per separare materie prime, generare chiavi di opportuni sistemi crittografici, sono problemi reali che si possono ricondurre al “Knapsack problem”.
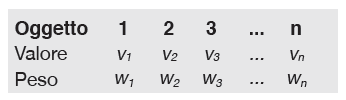
Formalizziamo il cosiddetto problema dello zaino 0-1: immaginate di star per tornare a casa al termine del vostro primo lungo viaggio all’estero dopo anni, quando all’aeroporto vi accorgete che la compagnia aerea ha abbassato il peso ammesso del bagaglio a mano. Non potete perdere il volo e, naturalmente, avete diversi souvenir che ora all’improvviso pesano troppo (e che fra qualche tempo riguarderete chiedendovi “ma perché ho comprato questo set di cani di porcellana così brutti?”). I vostri n oggetti hanno pesi w1, w2, ..., wn e valori v1, v2, ...vn:
Nel decidere cosa tenere nello zaino o lasciare in aeroporto, il vostro obiettivo è quello di massimizzare il valore degli oggetti che lasciate in valigia, rispettando il vincolo del peso e maledicendo le politiche di risparmio della compagnia aerea.
Si parla di problema 0-1 perché immaginiamo che i souvenir siano oggetti non divisibili, nel senso che si può decidere solamente se prenderli o no; non potete portare a casa solo la punta della meravigliosa Torre Eiffel in finto piombo, ad esempio. Immaginando di associare a ogni oggetto il valore 1 se l’oggetto è preso e 0 altrimenti, formalmente l’obiettivo è quello di calcolare il massimo di una data funzione di utilità:
sottoposta a un vincolo espresso nel seguente modo:
È chiaro che se gli oggetti sono pochi, ossia n è piccolo, la soluzione si trova con tranquillità. Al crescere di n il problema diventa, usando un eufemismo, non banale.
Ragioniamo insieme sulle possibili strategie per affrontarlo, continuando con l’esempio:
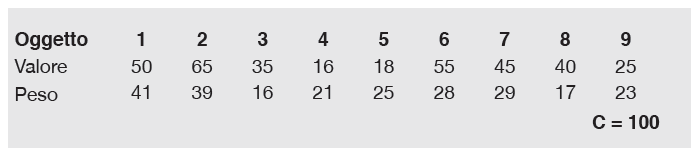
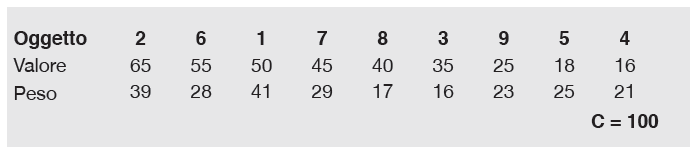
Abbiamo nove oggetti totali, con l’indicazione di valore e peso di ciascuno: per esempio, il primo oggetto ha valore 50 e peso 41 e, se scegliessimo di prenderlo, dovremmo scrivere che la variabile x1 è pari a 1, se volessimo escluderlo che è pari a 0. Con C indichiamo il vincolo, il peso massimo consentito, in questo caso 100.
Come già scritto in un articolo precedente (vedi sempre il numero 47 della rivista con l’articolo sulle formiche), l’approccio di forza bruta, detto anche di ricerca esaustiva, non è il migliore: in questo caso provare tutte le 512 possibilità, “prendo il primo sì e gli altri no, i primi due sì e gli altri no, il primo e il terzo sì...” e scegliere la migliore è un’operazione rapida al computer, ma in generale cercare la soluzione passando in rassegna ogni possibile configurazione risulta fattibile solo a livello teorico, in tempi che superano di molto l’età dell’universo se il problema è di vero interesse applicativo.
Bisogna cercare un criterio “furbo” per evitare di provare le strade inutili. Possiamo inizialmente farci guidare dal senso pratico, per poi affinare il nostro ragionamento, dato che, nella vita reale, non è sicuramente la ricerca esaustiva la prima strategia a venire in mente. È molto più probabile, infatti, che l’approccio pratico sia di tipo “greedy” (dall’inglese “ingordo”): ordinando gli oggetti da quello che “fa più gola” a quello “meno invitante”, si offre una modalità di decisione che, sperabilmente, condurrà a un buon risultato in tempo breve.
Ordiniamo quindi i nove elementi rispetto al loro valore, ottenendo la sequenza:
Questo approccio, sicuramente più rapido del primo, non è esente da difetti. Riuscite a notarli? L’oggetto 8 ha un valore “medio”, ma pesa pochissimo quindi forse non inserirlo è stato un errore... con questa modalità stiamo ignorando l’importanza del peso nella scelta. Non è possibile che, scegliendo due oggetti singolarmente di minor valore ma di più piccolo peso totale, si riesca ad ottenere un valore complessivo maggiore?
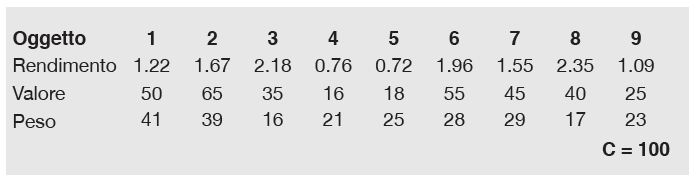
Come possiamo tener conto anche del peso nello scegliere l’oggetto? La risposta è valutare il rapporto “qualità-prezzo”, ossia creare una nuova lista che misuri il rendimento di ogni oggetto, definito come il rapporto fra il valore ed il peso:
rendimento = valore/peso.
Questa scelta, più oculata, offre la possibilità di trovare una soluzione mediamente migliore, ecco infatti la tabella con indicati i rendimenti:
Attenzione però!
L’approccio greedy è un approccio euristico, cioè non garantisce che la sequenza trovata sia sempre la migliore, barattando velocità e semplicità d’utilizzo per ottimalità della soluzione. Il problema dello zaino è un problema complesso, e “sufficientemente buono, ma non ottimo” è spesso un risultato sufficiente nelle applicazioni. Usando una terminologia più formale, ci troviamo di fronte a un problema NP-hard, che è un modo per dire che fa parte della classe dei problemi più difficili in assoluto nella teoria della computazione. Nel nostro esempio però possiamo tirare un respiro di sollievo: quella trovata dall’algoritmo ingordo è proprio la soluzione migliore.
Perlomeno, oggi possiamo vantarci del fatto che stavamo affrontando un noto problema di ottimizzazione matematica, chiamato appunto “problema dello zaino” (“Knapsack problem”, lo abbiamo già citato nel precedente articolo della rubrica dal titolo “Ottimizzazione, pensiero razionale...e formiche”).
Come sempre capita in matematica, la classe di problemi di cui parliamo è generale e non si riduce a preparare uno zaino o una valigia, esempi che fungono solo da modelli chiarificatori. Gestire le scorte di un magazzino, investire in pacchetti azionari, trovare la maniera meno dispendiosa per separare materie prime, generare chiavi di opportuni sistemi crittografici, sono problemi reali che si possono ricondurre al “Knapsack problem”.
Formalizziamo il cosiddetto problema dello zaino 0-1: immaginate di star per tornare a casa al termine del vostro primo lungo viaggio all’estero dopo anni, quando all’aeroporto vi accorgete che la compagnia aerea ha abbassato il peso ammesso del bagaglio a mano. Non potete perdere il volo e, naturalmente, avete diversi souvenir che ora all’improvviso pesano troppo (e che fra qualche tempo riguarderete chiedendovi “ma perché ho comprato questo set di cani di porcellana così brutti?”). I vostri n oggetti hanno pesi w1, w2, ..., wn e valori v1, v2, ...vn:
Nel decidere cosa tenere nello zaino o lasciare in aeroporto, il vostro obiettivo è quello di massimizzare il valore degli oggetti che lasciate in valigia, rispettando il vincolo del peso e maledicendo le politiche di risparmio della compagnia aerea.
Si parla di problema 0-1 perché immaginiamo che i souvenir siano oggetti non divisibili, nel senso che si può decidere solamente se prenderli o no; non potete portare a casa solo la punta della meravigliosa Torre Eiffel in finto piombo, ad esempio. Immaginando di associare a ogni oggetto il valore 1 se l’oggetto è preso e 0 altrimenti, formalmente l’obiettivo è quello di calcolare il massimo di una data funzione di utilità:
sottoposta a un vincolo espresso nel seguente modo:
È chiaro che se gli oggetti sono pochi, ossia n è piccolo, la soluzione si trova con tranquillità. Al crescere di n il problema diventa, usando un eufemismo, non banale.
Ragioniamo insieme sulle possibili strategie per affrontarlo, continuando con l’esempio:
Abbiamo nove oggetti totali, con l’indicazione di valore e peso di ciascuno: per esempio, il primo oggetto ha valore 50 e peso 41 e, se scegliessimo di prenderlo, dovremmo scrivere che la variabile x1 è pari a 1, se volessimo escluderlo che è pari a 0. Con C indichiamo il vincolo, il peso massimo consentito, in questo caso 100.
Come già scritto in un articolo precedente (vedi sempre il numero 47 della rivista con l’articolo sulle formiche), l’approccio di forza bruta, detto anche di ricerca esaustiva, non è il migliore: in questo caso provare tutte le 512 possibilità, “prendo il primo sì e gli altri no, i primi due sì e gli altri no, il primo e il terzo sì...” e scegliere la migliore è un’operazione rapida al computer, ma in generale cercare la soluzione passando in rassegna ogni possibile configurazione risulta fattibile solo a livello teorico, in tempi che superano di molto l’età dell’universo se il problema è di vero interesse applicativo.
Bisogna cercare un criterio “furbo” per evitare di provare le strade inutili. Possiamo inizialmente farci guidare dal senso pratico, per poi affinare il nostro ragionamento, dato che, nella vita reale, non è sicuramente la ricerca esaustiva la prima strategia a venire in mente. È molto più probabile, infatti, che l’approccio pratico sia di tipo “greedy” (dall’inglese “ingordo”): ordinando gli oggetti da quello che “fa più gola” a quello “meno invitante”, si offre una modalità di decisione che, sperabilmente, condurrà a un buon risultato in tempo breve.
Ordiniamo quindi i nove elementi rispetto al loro valore, ottenendo la sequenza:
- Il primo oggetto da aggiungere allo zaino è quello di valore 65, il secondo, che ha peso 39 (scriveremo che x2 = 1);
- scelto l’oggetto, verifichiamo che il peso totale sia minore di quello consentito (al primo passo la cosa è banale);
- procediamo quindi, in modo iterativo, scegliendo il successivo oggetto nella lista ordinata, ovvero quello di valore 55, x6 = 1;
- la somma dei pesi dei primi due oggetti non supera 100, dato che abbiamo 39+28 = 67, quindi possiamo ripetere;
- il successivo elemento è quello di valore 50, il primo, che però è troppo pesante. Scegliamo quindi il successivo in ordine (x7 = 1), arrivando a un peso complessivo di 96;
- non possiamo più proseguire, quindi scegliamo di portare con noi gli oggetti 2, 6 e 7, per un valore complessivo di 165.
Questo approccio, sicuramente più rapido del primo, non è esente da difetti. Riuscite a notarli? L’oggetto 8 ha un valore “medio”, ma pesa pochissimo quindi forse non inserirlo è stato un errore... con questa modalità stiamo ignorando l’importanza del peso nella scelta. Non è possibile che, scegliendo due oggetti singolarmente di minor valore ma di più piccolo peso totale, si riesca ad ottenere un valore complessivo maggiore?
Come possiamo tener conto anche del peso nello scegliere l’oggetto? La risposta è valutare il rapporto “qualità-prezzo”, ossia creare una nuova lista che misuri il rendimento di ogni oggetto, definito come il rapporto fra il valore ed il peso:
rendimento = valore/peso.
Questa scelta, più oculata, offre la possibilità di trovare una soluzione mediamente migliore, ecco infatti la tabella con indicati i rendimenti:
- Il primo oggetto da scegliere è proprio l’ottavo, che ha rendimento maggiore;
- il successivo è il terzo, per un peso totale di 17 + 16 = 33;
- con lo stesso ragionamento, aggiungiamo poi il sesto e il secondo oggetto;
- in questo modo, scegliendo gli oggetti 2, 3, 6 e 8, otteniamo un valore complessivo di 195, maggiore del precedente.
Attenzione però!
L’approccio greedy è un approccio euristico, cioè non garantisce che la sequenza trovata sia sempre la migliore, barattando velocità e semplicità d’utilizzo per ottimalità della soluzione. Il problema dello zaino è un problema complesso, e “sufficientemente buono, ma non ottimo” è spesso un risultato sufficiente nelle applicazioni. Usando una terminologia più formale, ci troviamo di fronte a un problema NP-hard, che è un modo per dire che fa parte della classe dei problemi più difficili in assoluto nella teoria della computazione. Nel nostro esempio però possiamo tirare un respiro di sollievo: quella trovata dall’algoritmo ingordo è proprio la soluzione migliore.
Note
- Silvano Martello and Paolo Toth. 1990. Knapsack problems: algorithms and computer implementations. John Wiley & Sons, Inc., USA.
- Jeff Erickson. Algorithms. Disponibile online qui: http://jeffe.cs.illinois.edu/teaching/algorithms/