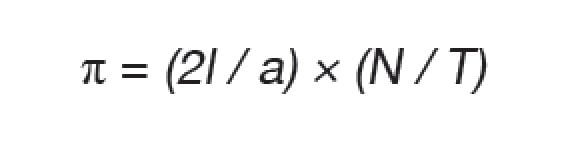L’italiano Mario Lazzarini disse nel 1901 di aver approssimato il valore di pi greco a sei cifre decimali grazie a un dispositivo meccanico. I matematici sono ancora furiosi.
Il redattore capo di Nature non trovò questo episodio divertente, e lo definì 'un’atrocità’: «Sia un ammonimento per tutti coloro che inquinano la letteratura che i loro misfatti li seguiranno nella tomba»[1].
L’ira di John Maddox, esplosa nell’agosto 1994, era stata innescata da un articolo del matematico americano Lee Badger, pubblicato quattro mesi prima. Badger, a sua volta, aveva studiato un articolo di un collega italiano pubblicato più di novant’anni prima e aveva determinato matematicamente che il risultato non poteva essere corretto: doveva esserci stata o una fortuna inimmaginabile o una frode (Il termine usato fu 'hoax’, beffa).
Quel collega era Mario Lazzarini, e il suo articolo del 1901 trattava di una determinazione sperimentale del numero pi greco, ben noto soprattutto nelle formule matematiche per la determinazione della circonferenza e dell’area del cerchio. Maddox era davvero sconvolto: «La verità è che se il risultato di Lazzarini fosse stato pubblicato nel 1994 e non nel 1901, sarebbe stato definito una palese truffa».
Il mio sospetto è che se Maddox avesse letto l’articolo di Lazzarini e non quello di Badger, più che furibondo sarebbe stato divertito.
L’idea di determinare il valore di pi greco sperimentalmente piuttosto che con calcoli matematici ha una lunga storia. Il diciottesimo secolo fu quello in cui i matematici scoprirono la teoria della probabilità – inizialmente applicata alle scommesse. Questa nuova branca forniva soluzioni a innumerevoli problemi che prima sembravano inattaccabili ma, naturalmente, diede anche origine a innumerevoli problemi nuovi. Uno fu proposto nel 1777 dallo studioso francese George-Louis Leclerc, conte di Buffon. Egli suggerì nel suo saggio morale Essai d’arithmétique morale:
Immaginiamo che in una stanza, dove il pavimento in parquet è costituito semplicemente da assi parallele, si lanci un sottile bastone e uno dei giocatori scommetta che il bastone non vada a toccare una delle fessure tra le assi del parquet, l’altro invece scommetta che il bastone lo faccia. Ci si chiede quale probabilità di vincita abbia ognuno dei giocatori.[2]
Buffon aggiunse che «si può giocare a questo gioco su una scacchiera con un ago da cucito o uno spillo senza testa». Con semplici calcoli, Buffon dimostrò che le probabilità per i due giocatori sono uguali se la lunghezza del bastone è di circa tre quarti della larghezza delle assi. Quindi estese il calcolo al caso di un bastone o di una moneta che cadano su un pavimento con piastrelle quadrate.
Quasi cinquant’anni dopo, nel 1812, il suo connazionale Pierre-Simon Laplace riprese il problema e, nella sua Théorie analytique des probabilités, poté calcolare la probabilità assoluta che «un cilindro molto sottile» toccasse una linea. Questo ovviamente dipende sia dalla lunghezza del cilindro che dalla distanza tra le linee.
Laplace chiamò la lunghezza del bastone 2r e la distanza tra due linee a. Se si lancia questo bastoncino un gran numero di volte, il rapporto tra il numero di volte in cui esso colpisce una linea e il numero totale di lanci sarà quasi uguale al valore 4r/aPIGRECO.
(I matematici iniziavano in quel periodo a indicare con il simbolo PIGRECO il rapporto tra circonferenza e raggio di un cerchio).
Questa formula non solo fornisce la soluzione al problema, ma anche un bel modo per determinare il valore di Pi greco per prove ed errori: se conosciamo la lunghezza del bastone e la distanza tra le linee, dopo molti lanci si potrà calcolare il valore di Pi greco.
Questo è leggermente diverso dal problema sulle probabilità di Buffon, ma oggi 'l’ago di Buffon' si riferisce al seguente esperimento: Si lancia un ago su una superficie rigata, si annota il numero di lanci N e il numero totale di Hit T (caso in cui l’ago tocchi una linea). Pi greco si calcola secondo la formula di Laplace (ove l è la lunghezza dell’ago, a la distanza tra le linee):
Quindi, ad esempio, se l’ago è lungo 25 millimetri e la distanza tra le linee è di 26 millimetri, dopo 100 lanci e 60 hit otteniamo una stima per Pi greco pari a 3,205128 (molte cifre decimali non hanno ovviamente senso, ne riparleremo più avanti).
Ci sono state davvero persone che hanno cercato di approssimare Pi greco in questo modo. Se avessero calcolato in anticipo il numero di tentativi necessari per ottenere anche solo la prima cifra decimale con ragionevole certezza, non avrebbero mai nemmeno provato, Nell’esempio riportato per un ago di 25 mm, si dovrebbero eseguire circa 8.000 lanci per avere una probabilità del 95% di ottenere un risultato tra 3,1 e 3,2. Se si vuole un decimale in più, i lanci devono essere 100 volte di più.
Ma non si deve mai sottovalutare la tenacia dei matematici.
Non menzioneremo tutti quegli eroi: nei libri di divulgazione scientifica troviamo M.A. Smith nel 1855 con 3.204 lanci e un Pi greco di 3,1553, August de Morgan con 600 lanci e 3,137, e un Capitano Fox americano che ottiene 3,1416 dopo 590 lanci. Quest’ultimo tentativo va sicuramente bene, dato il vero valore di Pi greco:
3,141 592 653 589 793 238 462 ...
Ma la medaglia per l’approccio più preciso andò, nel 1901, a Mario Lazzarini di cui sopra. Egli riportò, con 3.408 tiri e 1.808 hit, un’approssimazione sorprendentemente bella: 3,1415929, corretta alla sesta decimale.
Fu questo che suscitò le ire di John Maddox 93 anni dopo.
A prima vista il risultato sembra troppo bello per essere vero, e ovviamente l’affidabilità di Mario Lazzarini era già stata messa in dubbio prima che intervenissero Lee Badger e John Maddox. La cosa strana è che così tanti matematici abbiano preso sul serio le sue scoperte e abbiano visto in esse una bella illustrazione dell’ingegno matematico e sperimentale. Ancora una volta, non nomineremo tutti, ma nella letteratura troviamo nomi come George Gamow, Jacob Bronowski, Edward Kasner e James Newman. Gli ultimi due – veri matematici – nel loro libro del 1940, Mathematics and the imagination, scrissero entusiasti: «Difficile pensare di trovare un più bell’esempio dell’interconnessione di tutti i rami della matematica».
Il primo a sospettare degli ottimi risultati di Lazzarini, definendoli «maleodoranti», fu il matematico canadese Norman Gridgeman, in un articolo su Scripta Mathematica (vol. 25 (1960), 183–195).[3] Un anno dopo, l’8 giugno 1961, Thomas O’Beirne dedicò alla questione la sua rubrica del New Scientist "Puzzle e paradossi", senza conoscere l’articolo di Gridgeman.[4].
A poco a poco, l’ammirazione per Lazzarini andò calando, finché Lee Badger non diede il colpo finale con una pesante artiglieria matematica, in Mathematics Magazine, aprile 1994 (vol. 67, pp. 83-91).[5] Tutti avevano pensato più o meno velatamente che l’articolo fosse vergognoso, mettendo in dubbio l’onestà dell’italiano.
Mario Lazzarini pubblicò il suo articolo sul Periodico di matematica per l’insegnamento secondario (vol. 17 (1901), pp. 140–143).[6] Questo, come suggerisce il nome, non è una rivista di matematica, ma una rivista per insegnanti di matematica. Ciò è importante per il seguito; in tutti gli articoli su Lazzarini la rivista viene invariabilmente chiamata Periodico di matematica come se fosse un’autorevole rivista scientifica. Ed è anche dubbio che Lazzarini fosse davvero un 'matematico di professione', come viene sempre presentato: è più probabile che fosse un insegnante di matematica - probabilmente a Massa, in Toscana, secondo la firma di un altro articolo di sua mano sul Periodico.
Una ricerca di suoi ulteriori antecedenti, intrapresa per me dalla bibliotecaria italiana Ilaria Vercillo, non ha prodotto altre informazioni. Sembra che Lazzarini non abbia pubblicato nulla di scientifico se non alcuni articoli sul Periodico e un capitolo in un libro su Fibonacci; si è dissolto nella nebbia della storia della matematica.
In quella stessa nebbia, però, è scomparso anche l’intero apparato sperimentale di Lazzarini, il che è un peccato, perché avrebbe offerto ai suoi critici un'occasione in più per metterlo in cattiva luce. Gridgeman aveva già pronta la sua opinione ancora prima di leggere l’articolo di Lazzarini e racconta solo metà della storia (ma dubita che la macchina esistesse), e né O’Beirne né Badger si sono preoccupati di spiegare esattamente come gli esperimenti – e i risultati – di Lazzarini erano stati condotti.
Lazzarini invece lo spiega dettagliatamente nel suo articolo. Dice di aver costruito un dispositivo che automatizza completamente la caduta dell’ago e la registrazione dei risultati.
Nelle sue parole:
La prima cosa necessaria per poter fare un gran numero di osservazioni, colla massima sicurezza e col minor tempo possibile, era costruire un apparecchio capace di far cadere con sufficiente rapidità la sbarretta, e registrare automaticamente tanto il numero totale delle cadute, quanto il numero dei casi favorevoli.
L’apparecchio da me ideato, e del quale mi son servito per le esperienze di cui in seguito, consta di tre parti principali:
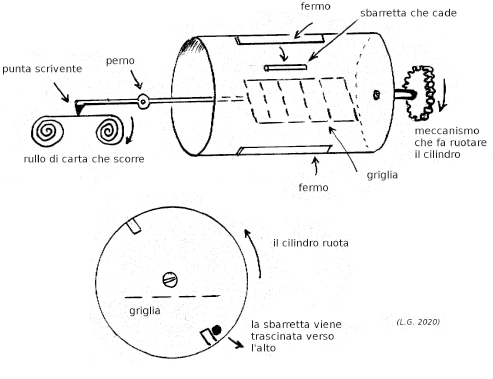
1. Un cilindro di lamiera di ferro sottile, dell’altezza di cm. 16 e del diametro alla base di cm. 17, aperto ad un’estremità e fissato per l’altra ad un asse, messo in rotazione da un movimento d’orologeria. Nell’interno di questa scatola cilindrica metto la sbarretta, la quale, mediante due arresti disposti internamente al cilindro stesso lungo due generatrici diametralmente opposte, viene per un certo tratto portata seco dal cilindro nella sua rotazione, e quindi lasciata cadere. Ma qui incontra l’altro arresto, che, a sua volta, la porta in alto e la rilascia cadere, avendosi così una serie non interrotta di cadute per tutto il tempo che dura la rotazione del cilindro. Un contatore, unito al movimento d’orologeria, indica il numero dei giri fatti dal cilindro stesso, e quindi anche, avendosi due cadute della sbarretta per ogni giro, il numero totale delle cadute. Nel mio caso, il cilindro compieva 12 giri al minuto, e quindi avevo 24 cadute della sbarretta.
2. La seconda parte dell’apparecchio da me usato, è quella che chiamerò la retina, consistente in un rettangolo di sottile filo di ferro, di cm. 8 di base e 15 di altezza di cui due lati opposti sono uniti mediante un sistema di fili di ferro sottilissimi, ben tesi, ed esattamente paralleli fra loro ed agli altri due lati del rettangolo. Questa retina vien posta orizzontalmente nell’interno della scatola cilindrica di cui sopra, e fa l’ufficio del sistema di rette parallele tracciate sulla carta, adoprato dagli altri, che, prima di me, si sono occupati dell’argomento.
3. Non rimane ora che registrare automaticamente il numero dei casi favorevoli. Per questo, la retina è portata da un’asta, mobile intorno ad un asse orizzontale, e fornita all’altro estremo di una punta scrivente. Un’apposita molla preme leggermente questa punta sopra una striscia di carta da telegrafi, che le è fatta scorrere sotto dallo stesso movimento d’orologeria che mette in moto il cilindro. La punta quindi viene a tracciare su questa striscia una linea continua. Supponiamo ora però che la sbarretta, di cui sopra, venga, nel cadere, ad urtare contro uno dei fili della retina: questa che, come ho detto, è mobilissima intorno ad un asse orizzontale, si abbassa, mentre dalla parte opposta la punta scrivente si alza, e la linea da essa tracciata rimane interrotta. Subito però la molla riconduce la punta in contatto colla carta, ed in questo modo ogni caso favorevole ci è segnalato da un’interruzione nella linea.
Così stando le cose, caricato una volta il movimento d’orologeria, possiamo abbandonare l’apparecchio a se stesso, non rimanendoci, alla fine dell’esperienza, che contare le interruzioni sulla striscia, e sostituire questo valore, insieme con quello datoci dal contatore del giri moltiplicato per 2, nella formula.
Ed ecco i risultati che Lazzarini ottenne con questo metodo.
Dapprima, dice, i fili sulla griglia erano paralleli all’asse del cilindro. Questa disposizione non funzionò molto bene: la distanza tra i fili era di 2,6 centimetri, e con 100 tentativi ebbe 60 hit, con 500 tentativi, 276. Questo dà stime per Pi greco di 3,205 e 3,484 (Lazzarini dà 3,483: sembra sempre troncare i valori invece di arrotondarli correttamente).
Lazzarini dice di avere ottenuto approssimazioni migliori girando i fili sulla retina di 90 gradi:
Ho avuto invece approssimazione maggiore col disporre la retina trasversalmente, vale a dire coll’unire tra loro i lati maggiori del rettangolo. Qui le esperienze vanno divise in due serie, giacché, mentre ho mantenuto sempre costante la lunghezza della sbarretta, ho fatto invece variare l’altezza della striscia compresa fra le parallele.
Ecco i risultati ottenuti:
1a serie: distanza tra i fili 2,6 cm
2a serie, distanza tra i fili 2,6 cm
Spicca immediatamente il risultato per 3.408 tiri. Non solo perché 3.408 non è una cifra tonda, ma anche perché Pi greco è stato improvvisamente calcolato con sette cifre decimali, mentre negli altri casi solo con tre o quattro. E le prime sei di quelle sette cifre decimali, come detto, sono corrette.
Sicuramente è inconcepibile che qualcuno dei colleghi insegnanti di Lazzarini avesse preso sul serio questo risultato. Tutto, veramente, punta nella direzione di una specie di scherzo, molto utile nelle lezioni di matematica, soprattutto se gli studenti hanno appena appreso l’ottima approssimazione a Pi greco ottenuta dalla frazione 355/113 che il matematico cinese Zu Chongzhi aveva già scoperto nel V secolo, e che era ben nota in Europa a partire dal 17esimo secolo. Infatti è questo che si ottiene dai calcoli di Lazzarini:
(3408/1808) × (5/3) = 355/113
La frazione 5/3 è, nella formula generale, 2l/a, ovvero il doppio della lunghezza del bastone di Lazzarini diviso per lo spazio tra i fili della 2a serie.
Sarà stato altrettanto chiaro, anche agli insegnanti di matematica all’inizio del secolo scorso, che questa precisione non aveva senso: se il numeratore e il denominatore hanno quattro cifre, la frazione decimale non dovrebbe avere sette cifre dopo il punto decimale. E anche ammettendo che la lunghezza della barretta e la distanza tra i fili fossero misurate con l’incredibile accuratezza di 0,1 mm, entrambe le misure non avrebbero avuto più di tre cifre significative. È quindi assurdo presentare il risultato finale con quattro, cinque, o addirittura otto cifre significative. E tralasciamo anche possibili errori nel calcolo degli hit e altri errori sperimentali.
Gli studenti avrebbero notato subito che la barretta non cadrebbe dal punto più alto del cilindro, ma rotolerebbe fuori dall’arresto quando il cilindro ha compiuto poco più di un quarto di giro dopo essere stata impegnata dal fermo nella posizione più bassa. Inoltre, la caduta della barretta avrebbe sempre avuto la forza necessaria per spostare la griglia e quindi sollevare la penna?
Un’altra condizione necessaria perché la formula di Laplace sia applicabile – forse un po’ difficile per gli studenti ma non per i loro insegnanti – è che l’ago che cade sia orientato casualmente, senza direzioni preferenziali. Come osservato da Gridgeman, l’apparecchio di Lazzarini non ha nulla che eviti una caduta preferenziale. Al contrario, sarebbero molto più probabili cadute della barretta più o meno parallele all’asse del cilindro.
Infine, l’intero esperimento sembra una fatica sprecata. Secondo Lazzarini, il suo dispositivo poteva effettuare 24 misurazioni al minuto; quindi, per 8.000 misurazioni, sarebbe stato utilizzato solo per sei ore. La cosa è sciocca sotto tutti i punti di vista.
Tuttavia, tutti i commentatori successivi omisero i dettagli dell'esperimento di Lazzarini e del pubblico di destinazione della rivista, e l’italiano sembrò colpevole di una seria frode scientifica.
Bridgeman e O’Beirne videro come il rapporto 355/113 fosse nascosto in 3408/1808, ma da matematici non si occuparono anche dei particolari pratici della strana macchina di Lazzarini, per cui sembrano non accorgersi della burla.
La maggior parte dei risultati di Lazzarini non differiscono affatto, o differiscono dal valore atteso solo di 1. In ognuno dei casi, la probabilità che avvenga è di poche unità per cento, e ciò significa che la probabilità di ottenerne così tanti e così prossimi al valore atteso è astronomicamente bassa.
Badger scrisse che «Col normale approccio alla distribuzione binomiale, la probabilità è minore di 0,000003». Come usare un cannone contro una zanzara.
Certo, non ci sono prove che Lazzarini stesse scherzando, e che avesse ideato una burla per scopi didattici, ma questa spiegazione sembra molto più plausibile di quella che avesse intenti malevoli. Negli anni ’80, gli scienziati iniziarono a rendersi conto che il loro santuario poteva essere utilizzato anche per delle frodi. Il libro di William Broad e Nicholas Wade, Betrayers of the Truth, fu pubblicato nel 1982, e lo stesso John Maddox aveva avuto dei problemi con gli errori scientifici di Jacques Benveniste nel 1988. Forse è per questo che tutti si sentirono molto colpiti.
Oggi, gli imbroglioni spudorati hanno sempre più problemi, e abbiamo anche acquisito maggiore familiarità con l’idea dello scherzo scientifico. Grazie ai numeri natalizi della rivista medica BMJ, sappiamo che la preghiera può guarire la setticemia e che l’«influenza maschile» è reale; ma anche altre riviste, perfino l’autorevole New England Journal of Medicine, a volte sconcertano i loro lettori con articoli scherzosi.
Forse tutta questa scienza scherzosa genera più confusione. Ma questo è un altro problema, sul quale Mario Lazzarini probabilmente avrebbe avuto qualcosa da dire.
Articolo tratto da: Skepter https://skepsis.nl/lazzarini/ . Si ringrazia l’autore per aver concesso il diritto di riproduzione. Traduzione di Luigi Garlaschelli, riveduta da Jan Willem Nienhuys. Hans van Maanen è direttore di Skepter da dicembre 2014.
Il redattore capo di Nature non trovò questo episodio divertente, e lo definì 'un’atrocità’: «Sia un ammonimento per tutti coloro che inquinano la letteratura che i loro misfatti li seguiranno nella tomba»[1].
L’ira di John Maddox, esplosa nell’agosto 1994, era stata innescata da un articolo del matematico americano Lee Badger, pubblicato quattro mesi prima. Badger, a sua volta, aveva studiato un articolo di un collega italiano pubblicato più di novant’anni prima e aveva determinato matematicamente che il risultato non poteva essere corretto: doveva esserci stata o una fortuna inimmaginabile o una frode (Il termine usato fu 'hoax’, beffa).
Quel collega era Mario Lazzarini, e il suo articolo del 1901 trattava di una determinazione sperimentale del numero pi greco, ben noto soprattutto nelle formule matematiche per la determinazione della circonferenza e dell’area del cerchio. Maddox era davvero sconvolto: «La verità è che se il risultato di Lazzarini fosse stato pubblicato nel 1994 e non nel 1901, sarebbe stato definito una palese truffa».
Il mio sospetto è che se Maddox avesse letto l’articolo di Lazzarini e non quello di Badger, più che furibondo sarebbe stato divertito.
Pavimento in parquet
L’idea di determinare il valore di pi greco sperimentalmente piuttosto che con calcoli matematici ha una lunga storia. Il diciottesimo secolo fu quello in cui i matematici scoprirono la teoria della probabilità – inizialmente applicata alle scommesse. Questa nuova branca forniva soluzioni a innumerevoli problemi che prima sembravano inattaccabili ma, naturalmente, diede anche origine a innumerevoli problemi nuovi. Uno fu proposto nel 1777 dallo studioso francese George-Louis Leclerc, conte di Buffon. Egli suggerì nel suo saggio morale Essai d’arithmétique morale:
Immaginiamo che in una stanza, dove il pavimento in parquet è costituito semplicemente da assi parallele, si lanci un sottile bastone e uno dei giocatori scommetta che il bastone non vada a toccare una delle fessure tra le assi del parquet, l’altro invece scommetta che il bastone lo faccia. Ci si chiede quale probabilità di vincita abbia ognuno dei giocatori.[2]
Buffon aggiunse che «si può giocare a questo gioco su una scacchiera con un ago da cucito o uno spillo senza testa». Con semplici calcoli, Buffon dimostrò che le probabilità per i due giocatori sono uguali se la lunghezza del bastone è di circa tre quarti della larghezza delle assi. Quindi estese il calcolo al caso di un bastone o di una moneta che cadano su un pavimento con piastrelle quadrate.
Quasi cinquant’anni dopo, nel 1812, il suo connazionale Pierre-Simon Laplace riprese il problema e, nella sua Théorie analytique des probabilités, poté calcolare la probabilità assoluta che «un cilindro molto sottile» toccasse una linea. Questo ovviamente dipende sia dalla lunghezza del cilindro che dalla distanza tra le linee.
Laplace chiamò la lunghezza del bastone 2r e la distanza tra due linee a. Se si lancia questo bastoncino un gran numero di volte, il rapporto tra il numero di volte in cui esso colpisce una linea e il numero totale di lanci sarà quasi uguale al valore 4r/aPIGRECO.
(I matematici iniziavano in quel periodo a indicare con il simbolo PIGRECO il rapporto tra circonferenza e raggio di un cerchio).
L’ago di Buffon
Questa formula non solo fornisce la soluzione al problema, ma anche un bel modo per determinare il valore di Pi greco per prove ed errori: se conosciamo la lunghezza del bastone e la distanza tra le linee, dopo molti lanci si potrà calcolare il valore di Pi greco.
Questo è leggermente diverso dal problema sulle probabilità di Buffon, ma oggi 'l’ago di Buffon' si riferisce al seguente esperimento: Si lancia un ago su una superficie rigata, si annota il numero di lanci N e il numero totale di Hit T (caso in cui l’ago tocchi una linea). Pi greco si calcola secondo la formula di Laplace (ove l è la lunghezza dell’ago, a la distanza tra le linee):
Quindi, ad esempio, se l’ago è lungo 25 millimetri e la distanza tra le linee è di 26 millimetri, dopo 100 lanci e 60 hit otteniamo una stima per Pi greco pari a 3,205128 (molte cifre decimali non hanno ovviamente senso, ne riparleremo più avanti).
Ci sono state davvero persone che hanno cercato di approssimare Pi greco in questo modo. Se avessero calcolato in anticipo il numero di tentativi necessari per ottenere anche solo la prima cifra decimale con ragionevole certezza, non avrebbero mai nemmeno provato, Nell’esempio riportato per un ago di 25 mm, si dovrebbero eseguire circa 8.000 lanci per avere una probabilità del 95% di ottenere un risultato tra 3,1 e 3,2. Se si vuole un decimale in più, i lanci devono essere 100 volte di più.
Ma non si deve mai sottovalutare la tenacia dei matematici.
Non menzioneremo tutti quegli eroi: nei libri di divulgazione scientifica troviamo M.A. Smith nel 1855 con 3.204 lanci e un Pi greco di 3,1553, August de Morgan con 600 lanci e 3,137, e un Capitano Fox americano che ottiene 3,1416 dopo 590 lanci. Quest’ultimo tentativo va sicuramente bene, dato il vero valore di Pi greco:
3,141 592 653 589 793 238 462 ...
Ma la medaglia per l’approccio più preciso andò, nel 1901, a Mario Lazzarini di cui sopra. Egli riportò, con 3.408 tiri e 1.808 hit, un’approssimazione sorprendentemente bella: 3,1415929, corretta alla sesta decimale.
Fu questo che suscitò le ire di John Maddox 93 anni dopo.
A prima vista il risultato sembra troppo bello per essere vero, e ovviamente l’affidabilità di Mario Lazzarini era già stata messa in dubbio prima che intervenissero Lee Badger e John Maddox. La cosa strana è che così tanti matematici abbiano preso sul serio le sue scoperte e abbiano visto in esse una bella illustrazione dell’ingegno matematico e sperimentale. Ancora una volta, non nomineremo tutti, ma nella letteratura troviamo nomi come George Gamow, Jacob Bronowski, Edward Kasner e James Newman. Gli ultimi due – veri matematici – nel loro libro del 1940, Mathematics and the imagination, scrissero entusiasti: «Difficile pensare di trovare un più bell’esempio dell’interconnessione di tutti i rami della matematica».
Puzza di imbroglio
Il primo a sospettare degli ottimi risultati di Lazzarini, definendoli «maleodoranti», fu il matematico canadese Norman Gridgeman, in un articolo su Scripta Mathematica (vol. 25 (1960), 183–195).[3] Un anno dopo, l’8 giugno 1961, Thomas O’Beirne dedicò alla questione la sua rubrica del New Scientist "Puzzle e paradossi", senza conoscere l’articolo di Gridgeman.[4].
A poco a poco, l’ammirazione per Lazzarini andò calando, finché Lee Badger non diede il colpo finale con una pesante artiglieria matematica, in Mathematics Magazine, aprile 1994 (vol. 67, pp. 83-91).[5] Tutti avevano pensato più o meno velatamente che l’articolo fosse vergognoso, mettendo in dubbio l’onestà dell’italiano.
Insegnanti di matematica
Mario Lazzarini pubblicò il suo articolo sul Periodico di matematica per l’insegnamento secondario (vol. 17 (1901), pp. 140–143).[6] Questo, come suggerisce il nome, non è una rivista di matematica, ma una rivista per insegnanti di matematica. Ciò è importante per il seguito; in tutti gli articoli su Lazzarini la rivista viene invariabilmente chiamata Periodico di matematica come se fosse un’autorevole rivista scientifica. Ed è anche dubbio che Lazzarini fosse davvero un 'matematico di professione', come viene sempre presentato: è più probabile che fosse un insegnante di matematica - probabilmente a Massa, in Toscana, secondo la firma di un altro articolo di sua mano sul Periodico.
Una ricerca di suoi ulteriori antecedenti, intrapresa per me dalla bibliotecaria italiana Ilaria Vercillo, non ha prodotto altre informazioni. Sembra che Lazzarini non abbia pubblicato nulla di scientifico se non alcuni articoli sul Periodico e un capitolo in un libro su Fibonacci; si è dissolto nella nebbia della storia della matematica.
Il cestello di una lavatrice
In quella stessa nebbia, però, è scomparso anche l’intero apparato sperimentale di Lazzarini, il che è un peccato, perché avrebbe offerto ai suoi critici un'occasione in più per metterlo in cattiva luce. Gridgeman aveva già pronta la sua opinione ancora prima di leggere l’articolo di Lazzarini e racconta solo metà della storia (ma dubita che la macchina esistesse), e né O’Beirne né Badger si sono preoccupati di spiegare esattamente come gli esperimenti – e i risultati – di Lazzarini erano stati condotti.
Lazzarini invece lo spiega dettagliatamente nel suo articolo. Dice di aver costruito un dispositivo che automatizza completamente la caduta dell’ago e la registrazione dei risultati.
Nelle sue parole:
La prima cosa necessaria per poter fare un gran numero di osservazioni, colla massima sicurezza e col minor tempo possibile, era costruire un apparecchio capace di far cadere con sufficiente rapidità la sbarretta, e registrare automaticamente tanto il numero totale delle cadute, quanto il numero dei casi favorevoli.
L’apparecchio da me ideato, e del quale mi son servito per le esperienze di cui in seguito, consta di tre parti principali:
1. Un cilindro di lamiera di ferro sottile, dell’altezza di cm. 16 e del diametro alla base di cm. 17, aperto ad un’estremità e fissato per l’altra ad un asse, messo in rotazione da un movimento d’orologeria. Nell’interno di questa scatola cilindrica metto la sbarretta, la quale, mediante due arresti disposti internamente al cilindro stesso lungo due generatrici diametralmente opposte, viene per un certo tratto portata seco dal cilindro nella sua rotazione, e quindi lasciata cadere. Ma qui incontra l’altro arresto, che, a sua volta, la porta in alto e la rilascia cadere, avendosi così una serie non interrotta di cadute per tutto il tempo che dura la rotazione del cilindro. Un contatore, unito al movimento d’orologeria, indica il numero dei giri fatti dal cilindro stesso, e quindi anche, avendosi due cadute della sbarretta per ogni giro, il numero totale delle cadute. Nel mio caso, il cilindro compieva 12 giri al minuto, e quindi avevo 24 cadute della sbarretta.
2. La seconda parte dell’apparecchio da me usato, è quella che chiamerò la retina, consistente in un rettangolo di sottile filo di ferro, di cm. 8 di base e 15 di altezza di cui due lati opposti sono uniti mediante un sistema di fili di ferro sottilissimi, ben tesi, ed esattamente paralleli fra loro ed agli altri due lati del rettangolo. Questa retina vien posta orizzontalmente nell’interno della scatola cilindrica di cui sopra, e fa l’ufficio del sistema di rette parallele tracciate sulla carta, adoprato dagli altri, che, prima di me, si sono occupati dell’argomento.
3. Non rimane ora che registrare automaticamente il numero dei casi favorevoli. Per questo, la retina è portata da un’asta, mobile intorno ad un asse orizzontale, e fornita all’altro estremo di una punta scrivente. Un’apposita molla preme leggermente questa punta sopra una striscia di carta da telegrafi, che le è fatta scorrere sotto dallo stesso movimento d’orologeria che mette in moto il cilindro. La punta quindi viene a tracciare su questa striscia una linea continua. Supponiamo ora però che la sbarretta, di cui sopra, venga, nel cadere, ad urtare contro uno dei fili della retina: questa che, come ho detto, è mobilissima intorno ad un asse orizzontale, si abbassa, mentre dalla parte opposta la punta scrivente si alza, e la linea da essa tracciata rimane interrotta. Subito però la molla riconduce la punta in contatto colla carta, ed in questo modo ogni caso favorevole ci è segnalato da un’interruzione nella linea.
Così stando le cose, caricato una volta il movimento d’orologeria, possiamo abbandonare l’apparecchio a se stesso, non rimanendoci, alla fine dell’esperienza, che contare le interruzioni sulla striscia, e sostituire questo valore, insieme con quello datoci dal contatore del giri moltiplicato per 2, nella formula.
Ed ecco i risultati che Lazzarini ottenne con questo metodo.
Dapprima, dice, i fili sulla griglia erano paralleli all’asse del cilindro. Questa disposizione non funzionò molto bene: la distanza tra i fili era di 2,6 centimetri, e con 100 tentativi ebbe 60 hit, con 500 tentativi, 276. Questo dà stime per Pi greco di 3,205 e 3,484 (Lazzarini dà 3,483: sembra sempre troncare i valori invece di arrotondarli correttamente).
Lazzarini dice di avere ottenuto approssimazioni migliori girando i fili sulla retina di 90 gradi:
Ho avuto invece approssimazione maggiore col disporre la retina trasversalmente, vale a dire coll’unire tra loro i lati maggiori del rettangolo. Qui le esperienze vanno divise in due serie, giacché, mentre ho mantenuto sempre costante la lunghezza della sbarretta, ho fatto invece variare l’altezza della striscia compresa fra le parallele.
Ecco i risultati ottenuti:
1a serie: distanza tra i fili 2,6 cm
| N | H | pi |
| 100 | 62 | 3,101 |
| 200 | 122 | 3.152 |
| 1000 | 611 | 3,147 |
| 2000 | 1229 | 3,126 |
| 3000 | 1840 | 3,135 |
| 4000 | 2448 | 3,142 |
2a serie, distanza tra i fili 2,6 cm
| N | H | pi |
| 100 | 53 | 3,144 |
| 200 | 107 | 3,115 |
| 1000 | 524 | 3,180 |
| 2000 | 1060 | 3,1446 |
| 3000 | 1591 | 3,142 |
| 3408 | 1808 | 3,1415929 |
| 4000 | 2122 | 3,1416 |
Spicca immediatamente il risultato per 3.408 tiri. Non solo perché 3.408 non è una cifra tonda, ma anche perché Pi greco è stato improvvisamente calcolato con sette cifre decimali, mentre negli altri casi solo con tre o quattro. E le prime sei di quelle sette cifre decimali, come detto, sono corrette.
Zu Chongzhi
Sicuramente è inconcepibile che qualcuno dei colleghi insegnanti di Lazzarini avesse preso sul serio questo risultato. Tutto, veramente, punta nella direzione di una specie di scherzo, molto utile nelle lezioni di matematica, soprattutto se gli studenti hanno appena appreso l’ottima approssimazione a Pi greco ottenuta dalla frazione 355/113 che il matematico cinese Zu Chongzhi aveva già scoperto nel V secolo, e che era ben nota in Europa a partire dal 17esimo secolo. Infatti è questo che si ottiene dai calcoli di Lazzarini:
(3408/1808) × (5/3) = 355/113
La frazione 5/3 è, nella formula generale, 2l/a, ovvero il doppio della lunghezza del bastone di Lazzarini diviso per lo spazio tra i fili della 2a serie.
Sarà stato altrettanto chiaro, anche agli insegnanti di matematica all’inizio del secolo scorso, che questa precisione non aveva senso: se il numeratore e il denominatore hanno quattro cifre, la frazione decimale non dovrebbe avere sette cifre dopo il punto decimale. E anche ammettendo che la lunghezza della barretta e la distanza tra i fili fossero misurate con l’incredibile accuratezza di 0,1 mm, entrambe le misure non avrebbero avuto più di tre cifre significative. È quindi assurdo presentare il risultato finale con quattro, cinque, o addirittura otto cifre significative. E tralasciamo anche possibili errori nel calcolo degli hit e altri errori sperimentali.
Gli studenti avrebbero notato subito che la barretta non cadrebbe dal punto più alto del cilindro, ma rotolerebbe fuori dall’arresto quando il cilindro ha compiuto poco più di un quarto di giro dopo essere stata impegnata dal fermo nella posizione più bassa. Inoltre, la caduta della barretta avrebbe sempre avuto la forza necessaria per spostare la griglia e quindi sollevare la penna?
Un’altra condizione necessaria perché la formula di Laplace sia applicabile – forse un po’ difficile per gli studenti ma non per i loro insegnanti – è che l’ago che cade sia orientato casualmente, senza direzioni preferenziali. Come osservato da Gridgeman, l’apparecchio di Lazzarini non ha nulla che eviti una caduta preferenziale. Al contrario, sarebbero molto più probabili cadute della barretta più o meno parallele all’asse del cilindro.
Infine, l’intero esperimento sembra una fatica sprecata. Secondo Lazzarini, il suo dispositivo poteva effettuare 24 misurazioni al minuto; quindi, per 8.000 misurazioni, sarebbe stato utilizzato solo per sei ore. La cosa è sciocca sotto tutti i punti di vista.
Tuttavia, tutti i commentatori successivi omisero i dettagli dell'esperimento di Lazzarini e del pubblico di destinazione della rivista, e l’italiano sembrò colpevole di una seria frode scientifica.
Bridgeman e O’Beirne videro come il rapporto 355/113 fosse nascosto in 3408/1808, ma da matematici non si occuparono anche dei particolari pratici della strana macchina di Lazzarini, per cui sembrano non accorgersi della burla.
La maggior parte dei risultati di Lazzarini non differiscono affatto, o differiscono dal valore atteso solo di 1. In ognuno dei casi, la probabilità che avvenga è di poche unità per cento, e ciò significa che la probabilità di ottenerne così tanti e così prossimi al valore atteso è astronomicamente bassa.
Badger scrisse che «Col normale approccio alla distribuzione binomiale, la probabilità è minore di 0,000003». Come usare un cannone contro una zanzara.
Scienza scherzosa
Certo, non ci sono prove che Lazzarini stesse scherzando, e che avesse ideato una burla per scopi didattici, ma questa spiegazione sembra molto più plausibile di quella che avesse intenti malevoli. Negli anni ’80, gli scienziati iniziarono a rendersi conto che il loro santuario poteva essere utilizzato anche per delle frodi. Il libro di William Broad e Nicholas Wade, Betrayers of the Truth, fu pubblicato nel 1982, e lo stesso John Maddox aveva avuto dei problemi con gli errori scientifici di Jacques Benveniste nel 1988. Forse è per questo che tutti si sentirono molto colpiti.
Oggi, gli imbroglioni spudorati hanno sempre più problemi, e abbiamo anche acquisito maggiore familiarità con l’idea dello scherzo scientifico. Grazie ai numeri natalizi della rivista medica BMJ, sappiamo che la preghiera può guarire la setticemia e che l’«influenza maschile» è reale; ma anche altre riviste, perfino l’autorevole New England Journal of Medicine, a volte sconcertano i loro lettori con articoli scherzosi.
Forse tutta questa scienza scherzosa genera più confusione. Ma questo è un altro problema, sul quale Mario Lazzarini probabilmente avrebbe avuto qualcosa da dire.
Articolo tratto da: Skepter https://skepsis.nl/lazzarini/ . Si ringrazia l’autore per aver concesso il diritto di riproduzione. Traduzione di Luigi Garlaschelli, riveduta da Jan Willem Nienhuys. Hans van Maanen è direttore di Skepter da dicembre 2014.
Note
1) 9 Maddox, J. False Calculation of pi by Experiment. Nature 370 (4 agosto 1994) p. 323. https://go.nature.com/3k2N78h
2) Je suppose que dans une chambre, dont le parquet est simplement divisé par des joints parallèles, on jette en l’air une baguette, & que l’un des joueurs parie que la baguette ne croisera aucune des parallèles du parquet, & que l’autre au contraire parie que la baguette croisera quelques-unes de ces parallèles; on demande le sort de ces deux joueurs.
3) Gridgeman, N. Geometric probablity an the number Pi. Scripta Mathematica dl. 25 (1960), p. 183–195.
4) 7 O’Beirne, T. Puzzles and Pardoxes – 23: how to Pi with statistics. New Scientist nr. 238 (8 juni 1961), p. 598. https://bit.ly/3vKAnI9
5) Badger, L. Lazzarini’s Lucky Approximation of Pi. Mathematics Magazine Vol. 67, No. 2 (april, 1994), pp. 83-91. https://bit.ly/3bbkYHl .
6) Lazzarini, M. Un’applicazione del calcolo delle probabilità – alla ricerca sperimentale di un valore approssimato di Pi greco. Periodico di matematica per l’insegnamento secondario. 17 (1901), p. 140–143. https://bit.ly/3wfy3sP