La statistica è lo strumento che ci permette di descrivere i dati e di prendere decisioni in caso di incertezza. Questa, ve ne sarete accorti, sta alla base della nostra quotidianità, tanto che senza la statistica non avremmo i test diagnostici, il controllo della qualità dei prodotti che compriamo, i social network, la meteorologia, il mondo assicurativo e autobus puntuali. La statistica è veramente ovunque, per dirla con le parole dello statistico britannico Karl Pearson è «la grammatica della scienza», in quanto può essere applicata ad ogni ambito. Ad esempio, grazie alla statistica possiamo ridurre le recidive dei carcerati, filtrare lo spam, intercettare frodi bancarie e principi di incendi o far riconoscere al telefono la vostra impronta digitale. Interagendo con la genetica gli statistici sono riusciti a ricostruire fenomeni complessi come le migrazioni e le relazioni all’interno di un ecosistema o a progettare algoritmi che – svelando la forma delle proteine – aiutano a capirne la funzione, spesso ancora sconosciuta. Insomma, sembra proprio vero che «Il bello di essere statistici è che si può giocare nel giardino di tutti gli altri», come diceva il matematico americano J.W. Tukey.
Ma, anche senza bisogno di addentrarci tanto, la statistica può aiutare ognuno di noi in svariate situazioni, tanto che la Divisione Statistica delle Nazioni Unite descrive il ruolo delle statistiche ufficiali come «elemento indispensabile nel sistema informativo di una società democratica». Anche l’ex presidente INPS, Tito Boeri, ha definito la statistica una «sentinella della democrazia». Ed è veramente così.
«Le informazioni statistiche riguardano la trasparenza: quando conosci la reale situazione del tuo Paese puoi chiederne conto al governo. I dati sono padre e madre per la democrazia», puntualizza Albina Chuwa, direttore generale dell’Ufficio di statistica nazionale della Tanzania[1].
Gli analisti hanno osservato che «di per sé le statistiche non portano benefici, ma è l’uso delle statistiche che offre vantaggi, permettendo al governo, alle aziende, alle organizzazioni non governative e ai singoli individui di prendere decisioni migliori e in tempi più rapidi[2]». Quando giornalisti, opinionisti o studiosi vogliono sapere cosa succede nel Paese si basano sempre sulle statistiche ufficiali. La Metropolitan Police di Londra, ad esempio, usa il censimento per individuare le strade dove vivono più cittadini anziani in modo da concentrare lì gli sforzi delle squadre incaricate di prevenire truffe e furti ai danni delle persone più vulnerabili. La Nuova Zelanda ha dimostrato come i dati forniti dal censimento permettano di allocare in maniera più efficiente le risorse per sanità e trasporti e in generale consentano politiche meglio calibrate[3].
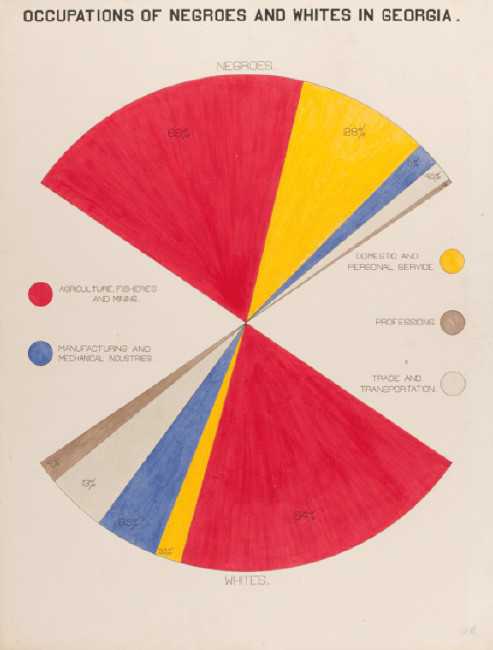
E le statistiche ufficiali sono a disposizione di ognuno di noi e sono gratuite. Basandosi su queste, lo storico Du Bois e il suo team realizzarono grafici magnifici che mostrarono all’Exposition Universelle del 1900 a Parigi, al fine di denunciare la drammatica situazione degli afroamericani negli Stati Uniti dell’epoca[4]. Un ottimo esempio di come saper maneggiare i dati possa servire a comprendere il mondo e, possibilmente, a migliorarlo.
Com’è quindi possibile che – in un periodo storico in cui si parla di sovraccarico informativo e di infodemia, in cui i dati sono resi pubblici e la stragrande maggioranza della popolazione è in grado di leggere e scrivere – esistano ancora persone che non si fidano dei risultati della statistica?
Secondo l’efficace sintesi di Gerd Gigerenzer: «Numbers are public, but the public is not generally numerate» (“I numeri sono pubblici, ma il pubblico generalmente non sa fare di conto”). Infatti, un motivo potrebbe essere la carenza di alfabetizzazione statistica (numeracy), dato che l’introduzione di questa materia nei curricula scolastici è piuttosto recente. Il nostro Paese non sembra essere cambiato molto da quando su la Repubblica leggevamo che «gli italiani, e in modo particolare i ragazzi, ignorano cosa faccia uno studioso di statistica. Per lo più, l’idea che hanno è quella di una specie di topo d’archivio che passa la sua vita a sbagliare sondaggi elettorali e a fare figuracce in tv»[5]. Inoltre, anche pratiche incoerenti, fonti dubbie e qualità dei dati eterogenea hanno contribuito a far vacillare la fiducia del pubblico nei dati.
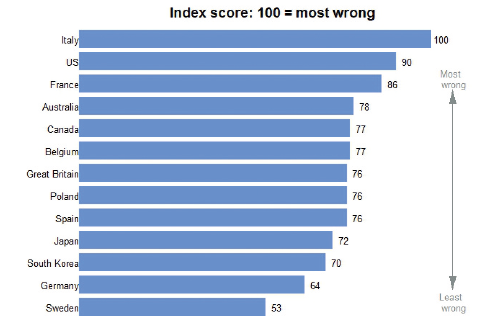
Che sia questo analfabetismo statistico la ragione per cui l’Italia risulta essere il Paese con la percezione più distorta della realtà in una classifica che confronta 13 nazioni occidentali[6]? Questo è il risultato di una ricerca che ha analizzato un campione di oltre 50 mila interviste realizzate negli ultimi cinque anni, e nella classifica siamo seguiti da Stati Uniti e Francia.
Dal numero di omicidi, fino all’incidenza del diabete e dell’immigrazione: «Ci sbagliamo quasi su tutto» scrive il direttore della sezione inglese dell’istituto di ricerca Ipsos, Bobby Duffy. L’Italia è per esempio il paese dell’Unione europea in cui c’è il maggiore divario tra gli immigrati “percepiti” e quelli realmente presenti sul territorio nazionale. Secondo quanto emerge dalla ricerca, la stragrande maggioranza dei cittadini italiani sovrastima la presenza di immigrati: a fronte di un 7% di stranieri presenti nel paese, gli italiani infatti ritengono che questi siano il 30%.
Perciò è fondamentale allenare la mentalità statistica, così da essere in grado di confrontare e analizzare informazioni significative in mezzo a un gran rumore di dati. Ecco quindi, nel caso ne sentiste il bisogno, qualche buon motivo per cui varrebbe la pena apprendere almeno le basi della statistica.
In questo periodo storico siamo particolarmente bombardati da dati che talvolta possono sembrarci imperscrutabili.
Consideriamo per esempio il risultato relativo ai decessi di persone positive alla variante Delta del Covid-19 in Inghilterra nel periodo tra il 21 giugno e il 12 settembre 2021: nella popolazione complessiva la percentuale dei non vaccinati morti era inferiore di circa 1.3 volte di quella dei vaccinati. Com’è possibile?
Tale fenomeno è spiegabile grazie al paradosso di Simpson, noto per essere la causa di molti errori di interpretazione. Secondo questo paradosso, quando si analizza una popolazione composta da diversi gruppi è possibile che all’interno di essi si evidenzi un fenomeno simile, mentre se guardiamo alla popolazione generale il fenomeno si capovolge, nel senso che emerge una relazione tra variabili opposta rispetto a quella reale.
Per esempio, se prendiamo in considerazione gli inglesi con meno di cinquant’anni scopriremo che la percentuale di decessi è inferiore nella popolazione vaccinata rispetto a quella non vaccinata. E lo stesso accade se analizziamo il sottogruppo degli inglesi sopra i cinquant’anni. Ma confrontare le percentuali nell’intera popolazione introduce una distorsione dovuta all’età e un modo per correggerla sarà quindi limitare il confronto per fasce d’età il più possibile omogenee per quanto riguarda il tasso di vaccinazione.
Un altro famoso esempio di questo paradosso è il caso dell’università di Berkeley, dove si osservò come il tasso di ammissione femminile fosse molto inferiore a quello maschile[7]. L’università avrebbe potuto venire accusata di discriminazione sessuale, quindi! Una più adeguata analisi dei dati mostrò che l’accusa era infondata: infatti, considerando i tassi di ammissione per dipartimento, la situazione era rovesciata, in quanto nella maggior parte dei dipartimenti le donne facevano registrare un tasso di ammissione più elevato. Magia? No, statistica.
Da due anni a questa parte siamo abituati a sentire i presentatori dei telegiornali dare letteralmente i numeri ogni giorno. Ma questi numeri snocciolati per regione, oltre a risvegliare in noi un forte senso di preoccupazione, hanno un senso? Spesso no.
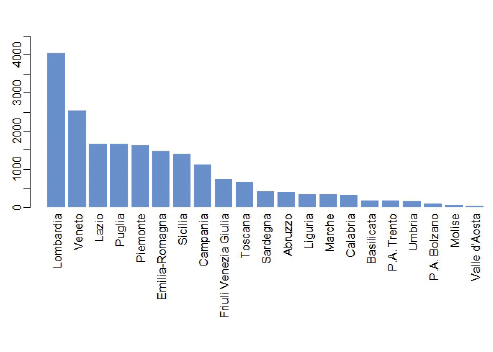
Il 1° dicembre 2020 la Lombardia era la regione con il maggior numero di nuovi casi di positivi al COVID-19, 4.048, seguita dal Veneto con 2.535 casi e dal Lazio con 1.669. Questa figura dà subito l’idea di come in Lombardia l’epidemia fosse molto più estesa rispetto alle altre regioni, mentre chi viveva in Friuli poteva stare tutto sommato tranquillo, essendo la regione posizionata verso metà classifica.
Ma la classifica risente della numerosità della popolazione nelle singole regioni, dato che a parità di diffusione del contagio una regione con il doppio degli abitanti rispetto a un’altra avrà anche il doppio di positivi. Ci sarà infatti una bella differenza tra avere duemila nuovi casi in Lombardia (che è la regione più popolosa d’Italia) o averli in Valle d’Aosta (che è invece l’ultima in classifica per quanto riguarda il numero di residenti). Non ha quindi alcun senso comunicare i numeri assoluti, mentre è molto più informativo fornire i numeri relativi, dividendo il numero di casi positivi per il numero degli abitanti.
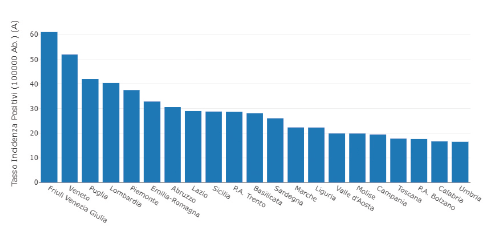
Ed ecco che il quadro cambia notevolmente, con la Lombardia che scivola al 4° posto e il Friuli che schizza al 1°, per un’incidenza (numero di nuovi casi) doppia rispetto al Lazio, pur avendo la metà dei positivi in numeri assoluti. Attenzione quindi a chi vi propone numeri assoluti: o non sa cosa sta facendo, o sta cercando di manipolarvi.
Un mondo senza distorsioni sarebbe meraviglioso, ma purtroppo in quello in cui viviamo queste abbondano. La distorsione (o bias) è una modifica, intenzionale o meno, del disegno e/o della conduzione di uno studio, dell’analisi e della valutazione dei dati, in grado di incidere sui risultati, portando a conclusioni sistematicamente diverse dalla verità. E ce n’è veramente per tutti i gusti: dal bias di progettazione a quello di allocazione, passando per quello di pubblicazione e di analisi, o nella valutazione, di frode della ricerca, o il bias di presentazione selettiva (su cui vi segnalo un video di Monty Python che lo spiega in modo inconsapevolmente divertente[8]), ecc.
Un famoso esempio di distorsione campionaria si è verificato alle elezioni presidenziali statunitensi del '36, alle quali concorrevano il governatore del Kansas, Alfred Mossman Landon e il democratico Franklin Delano Roosevelt. In quel periodo l’autorevole settimanale Literary Digest organizzò un sondaggio che venne inviato per posta a 10 milioni di persone. Sulla base delle risposte pervenute, che erano 2.4 milioni, predisse una vittoria per 3 a 2 per il candidato repubblicano, mentre lo statistico George Gallup (che negli anni Trenta essenzialmente inventò i sondaggi di opinione) ottenne un risultato opposto su un campione estremamente più esiguo di votanti e finì per avere ragione.
Roosevelt, infatti, non solo vinse, ma lo fece in modo schiacciante. L’errore del giornale fu quello di costruire il campione usando gli elenchi degli abbonati telefonici e dei proprietari di automobili, all’epoca beni poco diffusi. Questo fece sì che il campione fosse per lo più composto da cittadini benestanti e ciò produsse inevitabilmente risultati distorti, dato che i sostenitori di Roosevelt provenivano più che altro dalle classi meno abbienti. Inoltre, tutte le persone che non hanno risposto al sondaggio della rivista costituiscono quello che lo statistico David Hand definisce dark data, dati oscuri: le risposte mancanti. Sappiamo che le persone esistono ma non è dato sapere cosa pensino: possiamo ignorarle o tentare di far luce su ciò che manca, ma probabilmente il problema rimarrà.
Per poter generalizzare dal campione alla popolazione è cruciale che il campione sia rappresentativo, più che grande. Avere tanti dati non garantisce necessariamente la bontà del campione. Ne è un ulteriore esempio la società di sondaggi che nel 2015 fallì miseramente nel tentativo di prevedere i risultati delle elezioni britanniche, nonostante avesse intervistato migliaia di elettori. Successivamente un’inchiesta svelò come nel sondaggio telefonico la maggior parte dei numeri chiamati corrispondesse a telefoni fissi e che aveva risposto meno del 10% delle persone chiamate. Ecco quindi che difficilmente un campionamento di questo tipo potrà risultare rappresentativo. Questo tipo di problema ha afflitto anche i sondaggi del 2016 che davano Hillary Clinton in vantaggio rispetto a Donald Trump negli stati decisivi.[9]
Gallup trovò una buona analogia per sottolineare l'importanza del campionamento casuale dicendo che quando cuciniamo la zuppa in un pentolone non è necessario mangiarla tutta per capire se manca il sale: se mescoliamo a dovere basterà assaggiarne una cucchiaiata.
L’idea dell’importanza di un buon mescolamento si concretizzò nel 1969 nella lotteria della leva per la guerra in Vietnam dove, in base a una lista ordinata di date di nascita, sarebbero partiti prima gli uomini corrispondenti alle date in cima alla lista. Per cercare di rendere equa la selezione decisero di estrarre casualmente le date di nascita da una scatola, ma questa non fu mescolata e chi estraeva non infilò la mano sino in fondo.[10] In questo modo furono sfavoriti i nati nella seconda parte dell’anno.
Ma gli errori di campionamento sono infidi e si nascondono dappertutto, anche in studi ambiziosi come quello svedese che seguì più di 4 milioni di cittadini per oltre diciotto anni e arrivò a concludere che gli uomini con uno status socioeconomico più elevato avevano un tasso leggermente maggiore di tumori cerebrali. La notizia si trasformò nell’inquietante titolo giornalistico: Perché andare all’università aumenta i rischi di tumore cerebrale.[11] Che forse le sgobbate in biblioteca provochino qualche surriscaldamento nel cervello degli studiosi? Direi piuttosto che le persone benestanti e più istruite si interfacciano con medici migliori che gli procureranno una diagnosi prima e verranno così inserite nel registro dei casi di cancro.
Un esempio divertente è quello dello studio[12],[13], che mostrava i risultati ottenuti analizzando le lesioni riportate da alcuni gatti precipitati dai grattacieli di New York. Osservando i risultati non sorprende vedere che i gatti caduti dal quinto piano riportino più lesioni rispetto a quelli precipitati dal secondo, e che a quelli caduti dal settimo o ottavo vada ancora peggio. Ciò che ci stupisce è che oltre a queste altezze le cose sembrano migliorare: il numero medio di lesioni si riduce nei gatti precipitati dal nono piano in poi, tanto da avvicinarsi a quello osservato in gatti caduti dal secondo piano. Incredibile, non è vero? Gli autori giustificano lo strano fenomeno spiegando che, dopo aver raggiunto la velocità limite di caduta, il gatto si rilasserebbe e così facendo ammortizzerebbe l'impatto col suolo.
La spiegazione in realtà è molto meno romantica, in quanto l’inghippo sta nella costruzione del campione che era basato sui registri veterinari. Infatti, se un gatto cadeva dal ventesimo piano probabilmente, invece di essere condotto da un veterinario, finiva direttamente nel più vicino cimitero per animali. In questo specifico esempio il campione soffriva del bias di sopravvivenza, che induce ad attribuire a un numero esiguo di “sopravvissuti” il privilegio di rappresentare il gruppo molto più ampio al quale apparteneva originariamente.
Un altro esempio di bias di sopravvivenza risale al 1943, quando le forze armate statunitensi chiesero al matematico Abraham Wald un parere su come rendere più robusti i loro aerei. Capitava che questi tornassero dalle missioni con la fusoliera e le ali sforacchiate dai proiettili, aveva senso corazzare queste parti, dato che sembravano le più vulnerabili? Secondo Wald non veramente, infatti lui si chiese piuttosto cosa si sapeva degli aerei che non rientravano. Dato che raramente si erano osservati aerei di ritorno con danni a motori e serbatoi, forse quelle erano proprio le parti più sensibili ai danni fatali. Ma era semplicemente impossibile osservarle danneggiate in quanto in quei casi l’aereo non aveva scampo e veniva abbattuto.
Lo stesso errore lo commetteremmo se, vedendo che tre dei cinque studenti con i migliori voti all’università provengono dallo stesso liceo, credessimo che quel liceo offra un’istruzione migliore degli altri, perché in realtà si potrebbe semplicemente trattare di una scuola molto grande. Per poter valutare in modo oggettivo dovremmo valutare anche i voti degli studenti non “sopravvissuti” al processo di selezione.
Questo pregiudizio inficia il ragionamento anche di quel ristoratore che decida di aprire un nuovo locale in una tale città, confortato dai numerosi ristoranti di successo che vi operano. Infatti, così facendo, sta ignorando la possibilità che quei ristoranti di successo rappresentino solo la parte “sopravvissuta” di un insieme molto più ampio. Magari il 90% dei ristoranti aveva fallito durante il primo anno ma di loro lui non sa nulla dato che, per dirlo con le parole del saggista Nassim Nicholas Taleb, “il cimitero dei ristoranti falliti è molto silenzioso”.[14]
La specie umana è una “specie visiva”, il cui encefalo si è evoluto per elaborare le informazioni visive. Perciò l’occhio umano è per sua natura in grado di identificare in ciò che osserva andamenti regolari ed eccezioni ai pattern. Inoltre i numeri non parlano per sé ma sta a noi dar loro un significato. Ecco quindi perché al giorno d’oggi le rappresentazioni grafiche possono insinuarsi ovunque.
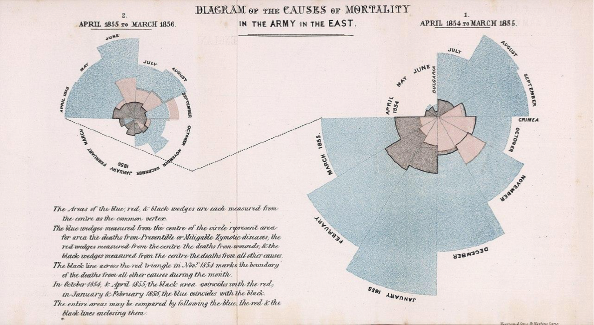
Ma due secoli fa, quando nacque Florence Nightingale, non era certamente così. Questa infermiera inglese allo scoppiare della guerra di Crimea fu inviata a dirigere una squadra di colleghe in un ospedale di Istanbul che versava in pessime condizioni. Florence, oltre a riorganizzare l’ospedale, iniziò ad annotare meticolosamente ogni dato rilevante a sua disposizione. Una volta rientrata in Inghilterra si rese conto dell’importanza di quei dati per comprendere meglio il problema e studiare delle soluzioni a riguardo. Serviva però un metodo per riassumere i principali problemi rilevati (come le infezioni, la malnutrizione e la mancanza di igiene) che non fosse la mera costruzione di noiose tabelle, spesso incomprensibili. Fu così che si inventò una sorta di istogramma circolare (diagramma della rosa) nel quale riuscì a sintetizzare le circa mille pagine di dati raccolti. Questi evidenziarono come la principale causa di morte dei soldati durante la guerra non fossero le ferite, bensì le malattie.
Lei, anche se incredula, richiese l’invio di una squadra di supporto per ripulire l’ospedale e nel 1877 arrivò dal Regno Unito una commissione sanitaria incaricata di dipingere le pareti, di rimuovere lo sporco e gli animali morti e di spurgare le fogne. Dopo il suo intervento sull’igiene in quell’ospedale la mortalità scese dal 42 al 2%.
Lei fu una delle prime persone al mondo a capire come un diagramma suscitasse reazioni molto più intense rispetto a una tabella piena di numeri e che una rappresentazione grafica, se ben pensata e organizzata, fa trapelare subito messaggi che dei semplici valori numerici non sono in grado di mostrare. Col passare del tempo, anche i medici fecero proprie le argomentazioni di Florence e attuarono dei provvedimenti in materia di igiene. Questa iniziativa si estese gradualmente fino a quando negli anni Settanta dell’Ottocento il parlamento approvò svariate leggi per promuovere la salute pubblica e la mortalità nel Regno Unito iniziò a calare, mentre parallelamente l’aspettativa di vita aumentò.
Fu così che Florence divenne la prima donna raffigurata su una banconota britannica, a parte la Regina. Per far fronte alla pandemia COVID-19, a Londra fu costruito un ospedale che porta il nome “Nightingale Hospital” in suo onore. La rivista Big Issue le ha dedicato la copertina del numero di marzo 2020 con un titolo che la acclamava per aver insegnato al mondo intero l’importanza di lavarsi le mani: un gesto che oggi riteniamo scontato, ma che non lo era affatto all’epoca, e che è stato anche il gesto fondamentale per combattere la pandemia in corso. Della grande Florence Nightingale dissero:
«Florence Nightingale credeva – e in tutte le azioni della sua vita agì con quella credenza – che l’amministratore può avere successo solo se guidato dalla conoscenza statistica. Il legislatore – per dire nulla del politico – sbagliava troppo spesso per la mancanza di questa conoscenza. No, lei è andata oltre; riteneva che tutto l’universo – comprese le comunità umane – si stava evolvendo secondo un piano divino; che lo scopo dell’uomo era sforzarsi di comprendere questo piano e guidare le proprie azioni in accordo con esso. Ma per comprendere i pensieri di Dio lei riteneva che dobbiamo studiare statistica, perché è quella la misura del Suo scopo. Quindi lo studio della statistica era per lei un dovere religioso.»[15]
Noi statistici la ricordiamo per aver dimostrato l’efficacia dei dati e averci aperto un nuovo canale di comunicazione complesso quanto utile. Nell’introduzione al suo libro Envisioning Information, l’information designer Edward Tufte ci mette in guardia: «I grafici richiedono una lettura attenta. Sono veri e propri scrigni traboccanti di significati, ma sono anche complessi e arguti». Perciò chiediamoci sempre quali, tra i mille grafici che ci bombardano ogni giorno, sono realmente attendibili e non manipolatori. Solitamente sono di contorno e tendono a distrarci, anche perché spesso vengono affidati al reparto grafico, con solida formazione artistica ma carente in quanto a competenze statistiche, mentre, come spiega il professor Alberto Cairo, «un buon grafico non è un’illustrazione bensì una spiegazione visiva».[16]
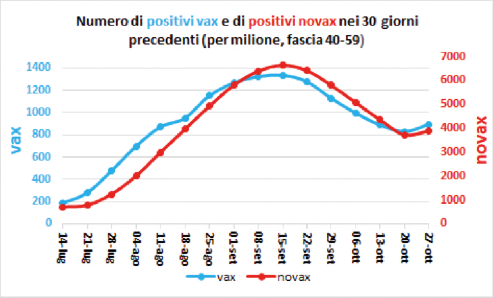
Un esempio particolarmente attuale di cattiva rappresentazione grafica è comparso nel tweet di una (sedicente) biologa molecolare dove sono disegnate due curve simili che rappresenterebbero i numeri di positivi tra vaccinati e non (per milione, fascia di età 40-59) per settimana nel periodo dal 14 luglio al 27 ottobre 2021.
Tale grafico veniva esibito allo scopo di dimostrare che il vaccino non servirebbe a proteggere dal contagio nella pandemia del COVID-19, dato che i positivi aumenterebbero in entrambi i gruppi e il trend sarebbe simile. Effettivamente le curve dei contagi sono altamente correlate, dato che se crescono i positivi tra i no-vax aumenteranno anche quelli tra i vaccinati, trattandosi di una malattia infettiva. Peccato però che la scala usata a destra per i no-vax era circa cinque volte quella usata a sinistra per i vaccinati. Saper leggere i grafici protegge anche da questi vecchi trucchetti ben noti a noi statistici.
Un sintomo della scarsa alfabetizzazione statistica nel nostro Paese è rappresentato – a mio avviso – dalla permanenza sui principali siti del lotto italiani[17],[18], degli elenchi dei cosiddetti “numeri ritardatari”, ovvero di quei numeri che non escono da diverse estrazioni. Secondo i sostenitori di questo metodo, la Legge dei grandi numeri assicurerebbe che a lungo termine ogni cifra verrà estratta con una frequenza pressappoco uguale, perciò quelli ritardatari dovranno necessariamente uscire più frequentemente in modo da recuperare la 'timidezza’ iniziale. Se così fosse, puntando su questi numeri timidi si avrebbe una maggiore probabilità di vincere.
Questa teoria avvincente non tiene purtroppo in considerazione il fatto che ogni estrazione è indipendente dalle precedenti, perciò ogni volta tutti i numeri avranno sempre la stessa probabilità di uscire, esattamente come ad ogni lancio di moneta si avrà sempre la stessa possibilità che esca testa o croce anche al secondo lancio, indipendentemente dal risultato appena ottenuto. Esattamente come il fatto di essere già sopravvissuti a un incidente aereo non ci potrà proteggere dall’infausto evento di ritrovarci nuovamente protagonisti di un altro incidente aereo. In statistichese diciamo che «l’urna non ha memoria».
La teoria dei numeri ritardatari, infatti, confonde la frequenza assoluta di un dato numero (cioè il numero di volte che questo è stato estratto) con la frequenza relativa (ovvero il rapporto tra le estrazioni di un numero e tutte le estrazioni). Soltanto quest’ultima è soggetta alla Legge dei grandi numeri e tende a bilanciarsi per ogni cifra, mentre le frequenze assolute (che sono quelle effettivamente pagate dal banco) possono anche divergere. Ad esempio, se dopo 100 lanci di una moneta sono uscite 40 teste e 60 croci, la teoria dei ritardi suggerisce di puntare sulle teste. Ma se dopo altri 900 lanci la situazione sarà di 450 teste e 550 croci, le frequenze relative si saranno avvicinate (proprio come stipulato dalla Legge dei grandi numeri) ma nei lanci supplementari il numero di croci uscite è stato ancora superiore.
Se oggi abbiamo queste conoscenze lo dobbiamo al cavaliere de Méré, giocatore accanito grazie ai cui dubbi nacque il Calcolo delle probabilità, disciplina che indica come l’unico modo per non perdere sia, semplicemente, non giocare.
Da uno studio sull’incidenza del cancro ai reni nelle 3141 contee statunitensi è emerso che quelle con l’incidenza di questa malattia più bassa erano per lo più rurali, poco popolate e situate in Stati tradizionalmente repubblicani del Midwest, del Sud e dell’Ovest. Come ve lo spiegate? Immagino abbiate escluso che la politica repubblicana sia una cura preventiva del cancro ai reni, più probabilmente sarete giunti anche voi alla conclusione plausibile che queste percentuali così basse siano dovute alla vita sana delle comunità rurali, dove l’inquinamento è sensibilmente minore e si ha accesso a cibi freschi e senza additivi.[19]
E se vi dicessi che le contee con un'incidenza più alta di questa malattia sono per lo più rurali, poco popolate e situate in Stati tradizionalmente repubblicani del Midwest, del Sud e dell’Ovest? Potrebbe essere causato dallo scarso accesso alle cure mediche, dall’alimentazione ricca di grassi e dal troppo consumo di alcol e tabacco? Ma com’è possibile che lo stile di vita rurale incida sia sull’alta che sulla bassa incidenza del cancro ai reni?
Si spiega con la spesso citata, purtroppo come abbiamo già visto a sproposito, Legge dei grandi numeri. L’abbiamo appena visto con i numeri del lotto, ma altri esempi potrebbero essere presi dal bar più vicino a casa, come: «Ieri c’è stato un incidente sulla tangenziale est, quindi per la legge dei grandi numeri è praticamente impossibile che se ne verifichi un altro» oppure «Il Parma ha vinto nove partite consecutive, quindi per la legge dei grandi numeri è altamente probabile che questa domenica perda». Tutto ciò non ha nulla a che vedere con questa povera legge, in quanto non esiste nessuna oscura tendenza compensatrice che spinga gli eventi in una direzione opposta a quella nella quale sono andati fino ad ora i fatti.
La legge dei grandi numeri afferma solo che, ad esempio, se peschiamo molte volte una carta da un mazzo, la probabilità di trovare proprio una certa carta (target) tende a coincidere col numero di carte uguali al target diviso per il numero totale di carte. In altre parole: i campioni più grandi forniscono stime più precise. Nella pratica, se volessimo una stima affidabile dell’altezza, tale legge suggerisce di misurare più persone possibili. La legge dell’acqua calda, non è vero?
Ecco perciò che se due persone si mettessero a prelevare biglie dallo stesso vaso che ne contiene sia rosse che bianche, ma una ne estraesse sempre quattro e l’altra sette per un numero di volte sufficientemente lungo, le estrazioni estreme (ovvero tutte bianche o tutte rosse) saranno molto più frequenti nei campioni da quattro, rispetto a quelli da sette. Quindi, se la popolazione statunitense fosse il vaso nel quale abbiamo città e contee e alcune biglie fossero contrassegnate dal cancro ai reni, invece che da un colore, i campioni rurali, più piccoli degli altri, sono più probabilmente soggetti a risultati estremi (incidenza molto elevata o molto bassa di tal cancro) rispetto ai campioni più grandi. Ecco quindi perché i risultati su campioni grandi sono più attendibili di quelli su campioni piccoli.
Esiste un numero che è in grado di misurare quanto due variabili si comportino nello stesso modo: si tratta del coefficiente di correlazione. La correlazione misura l’associazione tra due caratteristiche. Banalmente l’altezza correla col peso, dato che le persone più alte tendono generalmente a pesare di più. I nostri antenati, ad esempio, notarono che masticare la corteccia di salice alleviava i disturbi nelle persone che soffrivano di cefalea e di febbre. Da questa osservazione è nata l’invenzione dell'aspirina. Le correlazioni sono perciò indici potenti della possibile esistenza di una relazione causa-effetto.
Una pubblicazione su una rivista scientifica,[20] ad esempio, rivelava che le cicogne portano i bambini sulla base della correlazione tra numero di nati e numero di cicogne nei paesi europei. Ma sarà veramente così? Favole e leggende identificano la cicogna come animale beneaugurante, portatore di fecondità, ma si basano su un piccolo equivoco. Infatti, una volta, quando nasceva un bambino, in casa si accendeva il camino per più ore durante la giornata per scaldare l’ambiente. Se questo accadeva in primavera, le cicogne di ritorno dall’Africa, cercando il luogo più adatto per nidificare, optavano per il comignolo più caldo e quindi per quello della casa del neonato. Ecco perciò che sono i bambini a portare le cicogne e non viceversa!
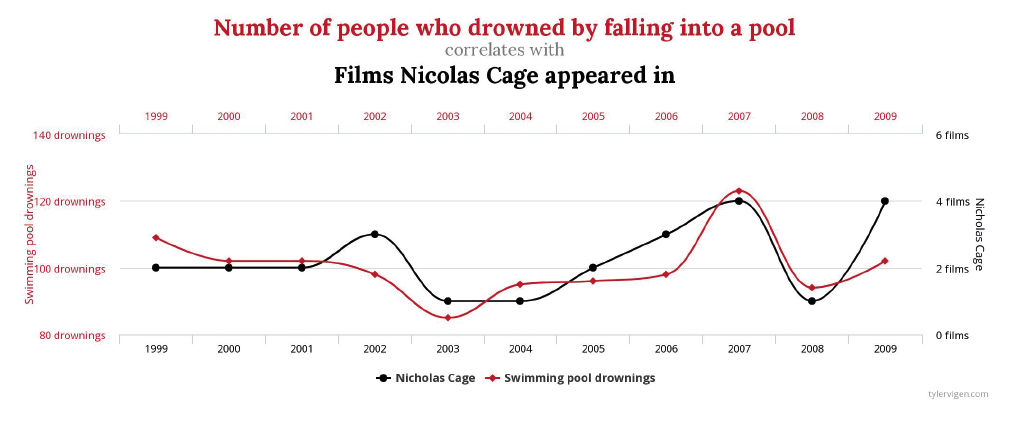
Esiste una sfilza di correlazioni molto alte tra variabili che intuitivamente non dovrebbero avere a che fare tra loro. Ne sono degli esempi il consumo di cioccolata pro-capite e il numero di premi Nobel per Stato, o il numero di persone che sono annegate cadendo in una piscina e i film in cui è apparso Nicolas Cage,[21] oppure ancora il tasso di divorzi nel Maine e il consumo pro-capite di margarina. Questo accade o per puro caso o perché tra le due variabili se ne nasconde una terza. Ad esempio, l’aspettativa di vita media degli abitanti di un Paese aumenta in funzione del numero di televisori pro-capite in quel Paese[22] non grazie ai poteri magici di guarigione da attribuire ai televisori, ma semplicemente perché il numero di televisori pro-capite e l’aspettativa di vita aumentano con la ricchezza complessiva del Paese. Così come qualsiasi correlazione tra le vendite di gelato e gli annegamenti è dovuta al fatto che i due fenomeni sono influenzati dalle condizioni meteo.
L’unica certezza è che lo stesso andamento di due variabili non significa che una sia causa dell’altra, cioè che la correlazione implichi un nesso casuale. Frase quest’ultima che dovremmo ripeterci come un mantra ogni mattina, dato che gli esseri umani hanno evidentemente una profonda necessità di spiegare gli avvenimenti con rapporti causa-effetto, sottovalutando la complessità del mondo in cui vivono. Tanto che è stato coniato un termine, apofenia, per indicare la tendenza a identificare nessi tra eventi non correlati tra loro.
Se gli esempi sino a qui mostrati erano piuttosto banali, vi assicuro che l’apofenia può nascondersi anche in casi più seri. Ad esempio, se vi dicessi che a molti bambini viene diagnosticato l’autismo poco dopo la somministrazione del vaccino combinato contro morbillo, parotite e rosolia, questo indicherebbe che i vaccini causano l’autismo? Un importante studio danese ha analizzato un campione di 650 mila bambini, gran parte dei quali avevano ricevuto il vaccino a 15 mesi d’età e un richiamo a 4 anni, mentre un campione più esiguo non ricevette alcuna dose. Molti bambini vaccinati ricevettero in effetti una diagnosi di autismo dopo la vaccinazione. Ma quando si guardarono i valori percentuali ci si accorse che la percentuale di diagnosi di autismo era la stessa in entrambi i gruppi. I due gruppi non differivano quindi dal punto di vista della presenza di diagnosi di autismo, in compenso la probabilità di contrarre le malattie sconfitte tramite quel prezioso vaccino era ovviamente più alta nel gruppo dei non vaccinati.[23]
Un altro esempio si trova nei decessi annuali: il fatto che la percentuale di mancini morti sia minore rispetto alla percentuale di mancini presenti nella popolazione totale proverebbe che i mancini vivono più a lungo? Forse dimostra soltanto che quando le persone che oggi muoiono erano piccole si obbligavano i bambini mancini a scrivere con la destra, così che i mancini anziani oggi sono rari. I papi muoiono a un’età media più avanzata rispetto alla media, ciò significa che diventare papa allunga la vita o che i papi vengono scelti quando hanno già un'età avanzata? Durante la Seconda guerra mondiale si notò che i bombardamenti alleati in Europa risultavano tanto più precisi quanto maggiore era il numero di caccia nemici decollati per intercettarli e quanto più intensa era la reazione della contraerea. In teoria sarebbe dovuto avvenire il contrario, se non fosse per il fatto che quando il cielo era nuvoloso i bombardieri avevano scarsa visibilità e per la stessa ragione la contraerea era minore. Un altro esempio è quello classico che lega il numero di vittime in un incendio a quello dei pompieri impiegati per spegnerlo: stranamente più pompieri si impiegavano, più vittime si registravano. Quindi si può pensare che impiegando meno pompieri si avrebbero meno vittime? Sarebbe splendido se fosse così, ma la cruda realtà è che entrambe le variabili dipendono da una terza: la dimensione dell’incendio.
Dato quindi che la correlazione non implica causalità, essa può solamente far sorgere in noi ipotesi che andranno però corroborate con studi progettati in maniera appropriata, così da poter giungere a conclusioni affidabili. Ed è proprio questo il lavoro che dovrebbe fare lo statistico, anche se spesso viene consultato solo quando si tratta di analizzare i dati raccolti, a frittata già fatta. Infatti, secondo una famosa affermazione del noto statistico Sir Ronald Fisher: «spesso consultare lo statistico dopo la conclusione di un esperimento equivale semplicemente a chiedergli di condurre un’autopsia. Al massimo potrà dire di che cosa è morto l’esperimento».
Supponiamo che a un folto gruppo di bambini siano state sottoposte due versioni equivalenti di un test attitudinale. Se selezioniamo dieci bambini fra quelli che hanno avuto una performance migliore in una delle due versioni, molto probabilmente scopriremo che il loro rendimento nell'altra versione sarà stato piuttosto deludente. Viceversa, se selezionassimo dieci bambini tra quelli che hanno avuto una performance più deludente ad un test, alla seconda versione otterranno probabilmente un risultato migliore. Nella quotidianità si verificano molto spesso casi come questo che illustrano il fenomeno noto col nome di regressione verso la media.
La regressione è sempre risultata indigesta alla mente umana, non a caso fu riconosciuta e compresa per la prima volta duecento anni dopo la legge di gravitazione universale e il calcolo differenziale. Secondo lo statistico David Freedman, se in una causa civile o penale saltasse fuori l’argomento della regressione, la parte che fosse costretta a spiegarlo alla giuria perderebbe il processo. Questo perché la nostra mente è fortemente incline alle spiegazioni causali e non è in grado di gestire bene i meri dati statistici.
Fu Sir Francis Galton, brillante cugino di Charles Darwin, il primo a osservare questo fenomeno. Fu anche l’inventore dello studio delle impronte digitali, colui che verificò se la preghiera aumentasse la durata della vita dei predicatori rispetto a quella degli altri individui e quantificò l’ereditarietà di molti caratteri importanti. Galton elaborò persino un’ipotesi sul fascino delle donne viste dal finestrino del treno diretto da Londra a Glasgow, trovando che il fascino diminuiva in funzione della distanza da Londra. Un tipino interessante deve essere stato tale Galton, la cui massima era «Quando potete, contate». Ma bando alle ciance, egli nel 1886 pubblicò l’articolo Regression towards mediocrity in hereditary stature (Regressione verso la mediocrità nella statura ereditaria) in cui parlava dei suoi studi che avevano riguardato sia le dimensioni di varie generazioni di semi che la statura di bambini confrontata con quella dei loro genitori. Dei primi scrisse:
«Risultava da questi esperimenti che i semi figli non tendevano ad avere dimensioni simili a quelle dei genitori, ma più mediocri (oggi diremmo più vicine alla media, NdR), ovvero tendevano a essere più piccoli dei genitori se i genitori erano grandi, e più grandi dei genitori se questi erano molto piccoli [...] Gli esperimenti hanno dimostrato inoltre che la regressione filiale media verso la mediocrità era direttamente proporzionale alla deviazione parentale da essa.»
Questo perché ogni volta che la correlazione tra due punteggi è imperfetta (ovvero quando all’aumentare di una variabile l’altra non aumenta o diminuisce in modo esattamente proporzionale) si verifica il bizzarro fenomeno della regressione verso la media, che ha una spiegazione, ma non una causa. L’evento che attira la nostra attenzione al torneo di calcetto è il frequente peggioramento della prestazione dei giocatori che avevano avuto molto successo all’inizio del torneo. La migliore spiegazione del fenomeno è che quei giocatori abbiano avuto un’insolita fortuna all’inizio, ma la nostra mente preferisce una spiegazione interessante che giri intorno a una causa. D’altronde, stareste ad ascoltare un giornalista economico che vi spiegasse (correttamente, peraltro) che l’economia quest’anno è andata meglio perché l’anno scorso era andata male? Ma è esattamente così che funzionano le fluttuazioni casuali.
Se leggeste sui giornali un titolo tipo questo: I bambini depressi cui viene somministrata con regolarità una bevanda energetica migliorano sensibilmente in circa tre mesi sareste indotti a concludere che la bevanda energetica abbia il merito del miglioramento osservato. Ma è altrettanto vero che si potrebbe osservare un miglioramento anche nei bambini depressi che passino del tempo a testa in giù o con in braccio un gatto. Ciò non toglie che dare il merito a tali fattori sia una conclusione ingiustificata, in quanto la correlazione tra punteggi di depressione nelle varie occasioni è imperfetta, perciò vulnerabile all’effetto della regressione verso la media. Pertanto, per poter affermare che una cura sia efficace bisognerà confrontare un gruppo di pazienti ai quali tale cura sia stata somministrata con un altro gruppo, detto di controllo, al quale non viene somministrata. Mentre il gruppo di controllo dovrebbe migliorare esclusivamente per effetto della regressione verso la media, i miglioramenti del secondo gruppo dovrebbero essere maggiori di quelli determinati dalla regressione verso la media di quel sottogruppo.
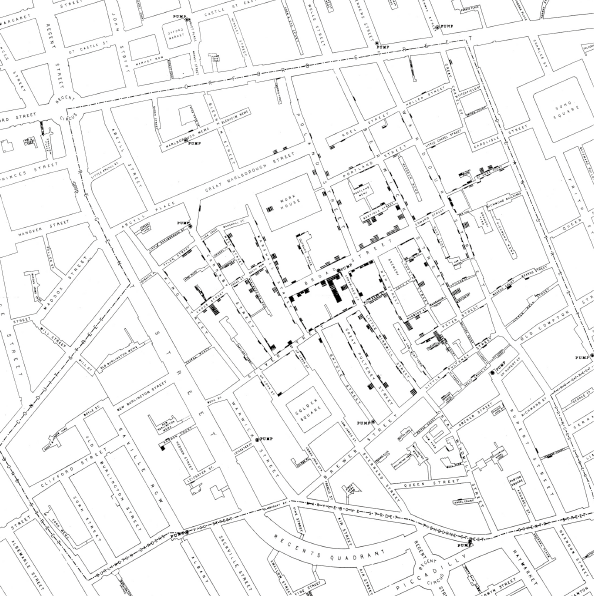
Anche senza entrare nell’ambito della misteriosa Biostatistica, ci sono diversi esempi di statistici che con le loro intuizioni hanno salvato numerose vite. Uno dei più celebri fu John Snow, che non c’entra evidentemente nulla con l’omonimo personaggio di Game of Thrones. Questo medico inglese, durante un’epidemia di colera scoppiata nel quartiere londinese di Soho, segnò su una mappa tutti i contagiati e gli balzò subito all'occhio che il maggior numero di casi era in prossimità della fontanella di Broad Street. Il sospetto che quello fosse il focolaio dell’infezione trovò conferma nel fatto che questa era alimentata da un pozzo (invece che dall’acquedotto) scavato in prossimità di una fossa biologica. Ebbe così l’idea rivoluzionaria (per quei tempi) che il colera non fosse un disturbo del sangue, bensì dell’apparato digerente, che si trattasse di una malattia contagiosa e che si diffondesse attraverso la via orale-fecale, attraverso l'acqua contaminata. Non appena riuscì a convincere le autorità a chiudere il pozzo incriminato l’epidemia si placò. Questo evento passò alla storia come la prima dimostrazione dell’efficacia delle mappe per comprendere l’evoluzione di un’epidemia e gettò le basi dell'epidemiologia moderna.
Un altro esempio, seppur diverso, è quello dello Space Shuttle Challenger che esplose nel 1986 subito dopo il lancio provocando la morte di tutto il personale che era a bordo. Causa? Un errore statistico. Infatti il lancio era stato pianificato in un giorno con una temperatura incredibilmente bassa, in quanto i dati non mostravano alcun nesso fra la temperatura dell’aria e i danni alle guarnizioni dei razzi. Non si erano accorti di un dettaglio però: e cioè che i dati erano incompleti, in quanto non consideravano i lanci in cui non si erano verificati danni, che si erano svolti quasi tutti con temperature più alte.
E anche voi, che siate statistici o meno, potreste aiutare i ricercatori dell’Istituto Fondazione Italiana per la Ricerca sul Cancro di Oncologia Molecolare a salvare delle vite umane, semplicemente scaricando sul vostro smartphone l’app DreamLab. Questa si attiverà mentre il telefono è in carica e, usando la potenza di calcolo del vostro dispositivo, aiuterà a velocizzare i complicatissimi calcoli che sono sempre più necessari negli studi oncologici e non solo. Se un progetto richiede circa 100 mila ore di calcolo per essere portato avanti (circa un anno e mezzo), basterà che un migliaio di persone mettano in carica il telefono per 6 ore al giorno con DreamLab installato per far calare il tempo di calcolo a meno di un mese.[24] È proprio il caso di dirlo: l’unione fa la forza.
Un'eclatante vicenda fu quella di Sally Clark, le cui due figlie di otto e undici settimane morirono in culla. Nonostante non fossero state trovate né prove né una possibile motivazione dell’omicidio, Clark nel 1998 fu accusata di duplice infanticidio dopo la testimonianza di un pediatra. Egli infatti fu chiamato a testimoniare in qualità di esperto e dichiarò che per la letteratura scientifica la morte in culla colpirebbe un bambino ogni 8.500, per cui la probabilità di tale evento è pari a 1/8.500. Alla domanda del giudice: Qual è la probabilità che due neonati muoiano per cause naturali? L’esperto rispose 1/8500 per 1/8500, cioè circa un caso su settantatré milioni. Verdetto della giuria: Sally Clark è colpevole!
Il problema è che non era corretto assumere che i due eventi fossero indipendenti (ovvero che l’avverarsi di uno non avesse interferito sul verificarsi dell’altro) e quindi non si potevano moltiplicare le rispettive probabilità, dato che fattori genetici e ambientali condivisi da membri della stessa famiglia aumentano le probabilità di morti in culla.
Inoltre, dalle statistiche ufficiali inglesi relative al 1997 si può osservare che la probabilità di due infanticidi compiuti dalla stessa persona era di circa uno su 2 miliardi. Era quindi molto meno probabile che Sally fosse colpevole piuttosto che innocente e proprio per questo Sally fu rilasciata ma non prima di aver scontato tre anni di carcere. Le tragedie della sua vita – la morte delle figlie prima e l’ingiusta condanna e carcerazione poi – possono aiutare a comprendere la causa della sua morte, un avvelenamento acuto da alcool, avvenuta a soli 42 anni.
Questo tipo di errore è noto col nome di fallacia dell’accusatore, dato che spesso ci si incappa nelle cause legali che si basano sui test del DNA. Ad esempio, quando uno specialista forense sostiene che se l’imputato è innocente c’è solo una probabilità su un miliardo che il suo DNA corrisponda a quello rinvenuto sulla scena del delitto. Ma poi interpreta questa affermazione in modo errato sostenendo che: «Dati gli indizi genetici, c’è solo una possibilità su un miliardo che l’imputato sia innocente». Questo è come sostenere che «se sei il papa sei cattolico» e saltare all'affermazione che «se sei cattolico sei il papa»”. Un errore logico più evidente, ma simile.
Un altro esempio di questa fallacia è emerso nella vicenda del campione di football americano O. J. Simpson, che fu assolto dall’accusa di aver ucciso l’ex moglie e il suo amante. Simpson aveva picchiato la moglie in almeno un’occasione ma il suo avvocato lo difese con i dati del Rapporto sulla Criminalità Ordinaria dell’FBI, secondo i quali su 4 milioni di donne picchiate dai compagni si sarebbero verificati solamente 1.432 omicidi. Perciò si attestava meno di un omicidio ogni 2.500 casi di maltrattamento. Quell'avvocato non doveva conoscere molto bene la statistica (o forse sì, e in tal caso ha approfittato dell’ignoranza del giudice), dato che – volendo risolvere il caso con la statistica – la probabilità da considerare era un’altra. Infatti, il ragionamento corretto da attuare in questo caso sarebbe stato: dato che una donna è stata assassinata e il suo compagno la picchiava, qual è la probabilità che sia stato lui ad ucciderla? Tale probabilità si calcola dividendo il totale delle donne uccise da chi le picchiava per il numero di donne picchiate e uccise. E tale probabilità è di circa il 90%. Una bella differenza.
I cervelli umani non elaborano molto bene le probabilità, come dimostra il fatto che tendiamo a giocare alla lotteria ma siamo spaventati quando saliamo su un aereo. Ci sono spiegazioni biologiche per questa tendenza, dato che sopravvalutare piccole probabilità che avrebbero esiti disastrosi ha aiutato i nostri antenati a sopravvivere. Ma nel mondo d’oggi, così dominato dall’incertezza, avere una mentalità statistica è sicuramente una caratteristica desiderabile che ci aiuta nella soluzione di problemi contro-intuitivi.
Un esempio lampante dell’innaturalità del pensiero probabilistico è il problema di Monty Hall, diventato particolarmente famoso dopo che nel film 21 Kevin Spacey lo propone alla sua classe. Si tratta di un gioco a premi in cui abbiamo di fronte tre porte chiuse e sappiamo che dietro a queste si nascondono due capre e una macchina, ma non sappiamo esattamente dove. Al giocatore viene chiesto di scegliere una delle porte, evento che avrà probabilità di successo (ammesso che siate interessati più a una nuova macchina che a una nuova capra) di un terzo. La porta che il giocatore ha scelto resterà chiusa e il conduttore del gioco – l’unico a conoscere la localizzazione del premio – aprirà una delle due rimanenti svelando una capra. A questo punto il conduttore offrirà al giocatore la possibilità di cambiare la sua scelta. Voi cosa fareste?
Saremmo intuitivamente portati a pensare che la probabilità di vincere la macchina sia sempre la stessa e perciò a non cambiare, ma non è così. Infatti, se rimanendo saldi alla nostra scelta iniziale la probabilità di ottenere una nuova macchina rimarrebbe di un terzo, il fatto di conoscere dove è posizionata una delle due capre fa sì che, cambiando, la probabilità di uscirne vittoriosi raddoppi. Ad essere onesti, dietro alla propensione a non cambiare c’è anche l’effetto psicologico per cui tendiamo a non cambiare la scelta già fatta per pigrizia, paura o per l'ancestrale convinzione che «chi lascia la via vecchia per la nuova, sa quel che lascia, e non sa quel che trova». Ma sarà veramente così?
Immaginate di aver commesso un crimine con un complice. La polizia vi arresta e vi confina in due celle separate, ma – non essendo in possesso di prove a sufficienza per condannarvi – vi propone il seguente accordo. Se entrambi confesserete vi verrà data una pena di sei mesi; nel caso in cui entrambi neghiate la pena sarà per entrambi di solo tre mesi di reclusione, poiché le prove non sono altro che indizi; mentre se uno confessa e l’altro nega, allora la pena verrà ridotta ad un solo mese per chi ha ammesso la propria responsabilità e sarà estesa ad un anno per chi non l’ha fatto. Voi come vi comportereste?
La scelta razionale sarebbe quella di negare, dato che solo in questo modo scontereste il minor tempo complessivo in prigione. Però negando correte il rischio che l’altro invece confessi e, tradendovi, vi faccia rinchiudere per il tempo più lungo. Come potete essere certi del fatto che il vostro complice non vi tradirà, dato che non potete comunicare? Il prezzo in palio è decisamente alto e i dubbi vi attanagliano. La paura vi porterà così a confessare, sperando che l’altro neghi e vi permetta di ridurre la vostra pena ad un mese. Questi stessi ragionamenti potrebbe farli però anche il vostro complice, che arriverebbe così alla vostra stessa conclusione, ovvero che negare e permettervi di incastrarlo è un rischio troppo grosso da assumersi. E così vi ritroverete rinchiusi in prigione per il doppio del tempo rispetto alla pena che vi sarebbe stata inflitta se aveste intrapreso la scelta razionale di negare entrambi. Capite quindi come tutto questo sia viziato dalla mancanza di fiducia.
Questo classico esperimento di teoria dei giochi, noto col nome di Dilemma del Prigioniero, fu inventato dal matematico statunitense Albert Tucker e presentato per la prima volta all’Università di Stanford nel 1950. Ci viene richiesto di decidere tra negare la nostra responsabilità lasciando che la colpa ricada solo sull’altro o cooperare con il nostro complice per ridurre la pena che subiremo. Noi sappiamo che la nostra civiltà si basa sulla collaborazione, ciononostante, generalmente si tende in primis a pensare al nostro rendiconto personale. Ecco quindi che, se la fiducia viene meno, le persone tendono a prendere decisioni da cui ipotizzano di trarre un vantaggio personale, ma che si rivelano negative per tutti. Questo dilemma è tuttora estremamente attuale e può essere usato per comprendere molte situazioni del mondo reale che si basano sulla fiducia.
Ad esempio, se ci fossero solo due case automobilistiche al mondo, il prezzo a cui una mette in vendita le proprie macchine avrà una ripercussione diretta sul prezzo a cui l’altra le venderà. Se una scegliesse di venderle a un prezzo più alto rispetto alla concorrenza, finirebbe per vendere meno auto. Mentre se decidesse di venderle a un prezzo inferiore, si aggiudicherebbe anche i clienti del concorrente, perciò venderebbe più auto ma con un margine di profitto inferiore. Certamente, anche l’altra casa automobilistica ragionerà allo stesso modo, con il risultato finale che entrambe otterranno scarsi profitti. Proprio come l’interesse personale spinge i prigionieri del dilemma all’atto controproducente di confessare, qui potrebbe rendere difficile per i due concorrenti adottare un comportamento cooperativo.
Questo dilemma, evidenziando il motivo per cui due soggetti potrebbero non cooperare anche quando è nell’interesse di entrambi, aiuta a comprendere l’inarrestabile corsa agli armamenti che contrappose USA e URSS. In quest’ultimo caso, sebbene la strategia migliore fosse evidentemente quella di limitare l’arsenale per scongiurare il pericolo di una nuova grande guerra, fu proprio la mancanza di fiducia a spingere i due blocchi ad accumulare più armi possibili. A pensarci bene, è la medesima logica che sta alla base del possesso di armi: gli individui possono scegliere se avere una pistola o meno, la ricerca mostra come le società siano più sicure quando nessuno possiede armi, tuttavia alcune persone temono che qualcun altro abbia un’arma. In tal caso, ciò li metterebbe in una posizione di svantaggio, spingendoli a portare con sé una pistola. Vedete come in ognuno di questi casi qualcuno agisce nel proprio interesse perché crede che anche gli altri lo faranno.
In pratica, il dilemma del prigioniero dimostra che, quando gli individui perseguono solo il proprio interesse personale in un ambiente in cui il guadagno dipende anche dalle decisioni prese dagli altri, il risultato sarà peggiore rispetto a quello che avrebbero ottenuto nel caso in cui avessero cooperato. In un’epoca in cui le nostre vite sono caratterizzate come non mai dall’interdipendenza, è chiaro come questo dilemma possa insegnarci l’importanza di una collaborazione, sia nell’emissione di linee guida nazionali che nelle nostre azioni personali. Ad esempio, se indossare una mascherina riduce la quantità di goccioline nell’aria che si diffondono su una persona o che contaminano le superfici, il fatto di non indossarla mentre gli altri prendono questa precauzione avrà un impatto negativo sulla loro efficacia. Allo stesso modo, i paesi ricchi sfavorendo quelli poveri nell’accesso ai vaccini non stanno adottando la soluzione migliore, ma aggravano le disuguaglianze e contribuiscono all’emergere di nuove varianti del virus.
Come scrive il professore di Stanford Matthew Jackson: «Proprio come non puoi curare un’infestazione da termiti fumigando solo una stanza in una casa, non si può controllare la pandemia del Coronavirus indirizzando gli interventi a una regione o un paese specifico».[25]
Se a breve termine l’accumulo di vaccini può sembrare una vittoria per un Paese, si tratta di una perdita per altri. Se tutti i Paesi cooperano, il mondo può ottenere il risultato di sconfiggere la pandemia. Se non collaborano, il Covid si trascinerà e ci saranno inevitabilmente molti più decessi.
Siamo insomma di fronte all’eterno dilemma etico fra Callicle, che sosteneva la legge del più forte, e Socrate, secondo il quale la giustizia richiede cooperazione e una visione che comprenda sia i forti che i deboli. Nel nostro contesto pandemico, Callicle si chiederebbe: perché i politici dei paesi ricchi non dovrebbero acquistare i vaccini e dare prima l’immunità di gregge ai propri elettori? Mentre per Socrate il mondo starebbe meglio se li condividessimo, in quanto la mia sopravvivenza è interconnessa alla tua salute. E la scienza è dalla parte di Socrate.
La scarsa educazione al metodo statistico gioca un ruolo anche nel fenomeno dell’analfabetismo funzionale - ovvero di chi sa leggere e scrivere, ma ha difficoltà a comprendere testi semplici (literacy) ed è privo di molte delle competenze di calcolo (numeracy) utili alla vita quotidiana. E c’è chi approfitta di questo nostro tallone d’Achille. Per esempio Ryanair, che nel 2017 annunciò che il 92% dei suoi passeggeri si era dichiarato soddisfatto di aver volato con loro. Il problema è che il sondaggio prevedeva solamente le seguenti possibili risposte: eccellente, ottimo, buono, soddisfacente e passabile.[26]
O di come molti mass-media riportarono l’inchiesta di qualche anno fa (documentata nel libro Wehler, C. A. (1991). A survey of childhood hunger in the United States. Community Childhood Hunger Identification Project) che rivelava che 11,5 milioni di bambini statunitensi rischiavano di morire di fame.[27] In seguito si scoprì che erano stati giudicati a rischio se i loro genitori avevano risposto affermativamente almeno a una domanda di un gruppo di otto tra cui: «Ha mai avuto problemi a nutrire i suoi figli perché stava finendo i soldi?».
In un articolo apparso su Internazionale il giornalista inglese David Randall elencò alcune affermazioni clamorose, come quella secondo cui «sono più gli afroamericani in prigione di quelli che frequentano un college». Considerando che i detenuti possono avere tra i 16 e i 96 anni, mentre l’età degli studenti universitari generalmente va dai 18 ai 23 anni, si vede che in realtà tra gli afroamericani di quest'ultima fascia d’età gli studenti universitari sono quasi il triplo dei detenuti.[28] Un altro esempio analogo riguarda una denuncia che nel 1997 venne formulata contro un laboratorio sostenendo che il 29% degli ex dipendenti era morto di cancro. Inquietante? Non proprio, dato che il cancro è la causa di morte del 35% delle persone tra 44 e 65 anni.
Dobbiamo tenere presente che i titoli sensazionali dei giornali cercano di stuzzicare la nostra curiosità. Con interpretazioni allarmistiche dei dati tentano di fare più colpo sul lettore. Il pezzo, pubblicato sul Corriere della Sera del 25 agosto 2003, intitolato: Gli automobilisti corretti? Solo l’8% ne è un esempio. Dal titolo siamo portati a concludere che quasi tutti gli automobilisti siano scorretti, quando in realtà i dati su cui si basava l’articolo e che categorizzavano gli automobilisti in base alla correttezza della guida, sono i seguenti: guidatori corretti (8%); guidatori non completamente corretti (86%); guidatori scorretti (6%). Quindi un titolo altrettanto parziale e veritiero rispetto a quello scelto avrebbe potuto essere: Gli automobilisti scorretti? Solo il 6%. E avrebbe trasmesso l’informazione opposta. Questo perché un dato decontestualizzato è veritiero quanto un fotogramma ritoccato.
Il problema non riguarda peraltro solo i mass-media: uno studio ha rilevato che nel 40% dei 462 comunicati stampa delle università britanniche pubblicati nel 2011 si trovano consigli esagerati, nel 33% nessi causali esagerati e nel 36% sono state rilevate conclusioni esagerate relative agli esseri umani partendo da studi sugli animali.[29] Più o meno strumentalmente, quindi, ricercatori e uffici stampa, giornalisti e commentatori forzano talvolta la lettura e l’interpretazione dei dati statistici, perpetuando quella che il prof. Milo Schield chiama prevaricazione statistica, e che consiste «nell’alterare la verità attraverso un’ambiguità, un equivoco o un’omissione».[30]
Non fraintendetemi, esiste un giornalismo scientifico di qualità, ma ne esiste anche uno scadente. Per distinguerli dopo aver letto un articolo, provate a chiedervi come potreste riassumerlo ad un amico. Avete capito cosa hanno fatto i ricercatori e perché? Cosa veniva misurato? Lo studio era stato effettuato su umani o su cavie? Il risultato era inatteso per la comunità scientifica? Un bravo giornalista deve specificarlo.
Un sensazionale esempio di prevaricazione statistica si presentò quando l’Agenzia internazionale per la ricerca sul cancro dell'OMS (IARC) annunciò che la carne lavorata rientrava nel gruppo I delle sostanze cancerogene, la stessa delle sigarette e dell’amianto. Ed ecco che una mattina ci siamo svegliati con l’articolo de Il Fatto Quotidiano intitolato: “Alimenti cancerogeni, Oms: 'Wurstel, prosciutto e carni lavorate possono causare il cancro. Dannosi come il fumo’”. L’IARC ha tentato poi di spiegare che tale classificazione è dovuta alla certezza di un maggiore rischio di cancro, e che l’assunzione quotidiana di 50 grammi di carne lavorata è associata ad un aumento del 18% del rischio di tumore del colon-retto. Ciò significa che se ci si aspettano 6 casi di tumore del colon-retto su 100 persone che non mangiano quotidianamente carne lavorata, ci aspettiamo un caso in più tra altre 100 simili ma con una passione sfrenata per i wurstel. Avete capito la portata dello scoop ora?
Uno studio[31] ha dimostrato che gli incidenti automobilistici aumenterebbero significativamente nei periodi di luna piena e ovviamente questo risultato ha attratto l’attenzione dei media, in quanto ha fatto subito pensare a vicende di lupi mannari e vampiri. Ma tale aumento era solo dell’1%, troppo piccolo quindi per indurci a lasciare la macchina a casa quando la luna splende piena in cielo.
All’inizio del secolo scorso, col termine “significativo” si intendeva che qualcosa significava o mostrava un concetto. Per lo statistico Ronald Aylmer Fisher un risultato significativo si aveva quando i dati indicavano una certa differenza dall’ipotesi che voleva confutare. Al giorno d’oggi il termine “significativo” tende ad essere confuso col termine “importante” e ciò crea ambiguità. Ad esempio, se un articolo giornalistico descrive un nuovo risultato scientifico come un “nuovo risultato significativo” o un “progresso significativo nella nostra conoscenza”, si tratterà di un enunciato statistico oppure di un giudizio di valore? Spesso il significato si confonde, dato che un risultato statisticamente significativo non è sinonimo di un risultato rilevante.
Effetti minuscoli e irrilevanti possono risultare statisticamente significativi se si ha a disposizione un campione molto grande, ecco perché è buona prassi ambire a dimostrare differenze importanti. D’altra parte, un risultato può essere importante anche se non è statisticamente significativo, come quando nuovi dati suggeriscono un pattern che, se verificato, potrebbe essere importante per capire un fenomeno sconosciuto e indurre quindi ad approfondire uno studio. Come è successo, ad esempio, quando uno studio su larga scala sull’efficacia della terapia ormonale sostitutiva (TOS) non ha mostrato evidenze statisticamente significative del beneficio della TOS sulle donne in post-menopausa.
Questa terapia era stata ampiamente usata, anche con un notevole investimento di denaro e con alcuni effetti collaterali deleteri; perciò scoprire che era di scarso beneficio ha permesso di risparmiare una grande quantità di risorse e di prevenire questi effetti collaterali. Questo risultato non era statisticamente significativo, ma fu decisamente importante.
In altri casi invece l’associazione può essere statisticamente significativa... senza che questo significhi davvero qualcosa. Simonsohn e i suoi colleghi[32] chiesero ad alcuni studenti dell’Università della Pennsylvania di ascoltare “When I’m sixty-Four” dei Beatles, oppure “Kalimba” o “Hot Potato” dei Wiggles per poi chiedere loro l’età. Ripetendo le analisi dei dati in ogni modo possibile e continuando ad aggiungere soggetti allo studio, alla fine Simonsohn riuscì ad ottenere un’associazione significativa, dimostrando così che ascoltare la canzone dei Beatles renderebbe più giovani. Lo scopo dei ricercatori in questo caso era proprio quello di dimostrare che – citando lo scrittore Gregg Easterbrook – «Se torturi i numeri abbastanza a lungo, confesseranno qualsiasi cosa»
La poesia che Trilussa dedicò qualche secolo fa alla statistica è molto conosciuta:
Sai ched’è la statistica? È na’ cosa
che serve pe fà un conto in generale
de la gente che nasce, che sta male,
che more, che va in carcere e che spósa.
Ma pè me la statistica curiosa
è dove c’entra la percentuale,
pè via che, lì, la media è sempre eguale
puro co’ la persona bisognosa.
Me spiego: da li conti che se fanno
seconno le statistiche d’adesso
risurta che te tocca un pollo all’anno:
e, se nun entra nelle spese tue,
t’entra ne la statistica lo stesso
perch’è c’è un antro che ne magna due.
Er compagno scompagno:
Io che conosco bene l’idee tue
so’ certo che quer pollo che te magni,
se vengo giù, sarà diviso in due:
mezzo a te, mezzo a me... Semo compagni.
No, no - rispose er Gatto senza core -
io non divido gnente co’ nessuno:
fo er socialista quanno sto a diggiuno,
ma quanno magno so’ conservatore.
Questo sonetto divertente ed elegante è ben poco generoso con la statistica e con una delle sue misurazioni più spesso utilizzate: la media. Sulla povera media aritmetica circolano vecchie battute secondo le quali quasi tutti hanno un numero di gambe maggiore della media (probabilmente vicina a 1.99999) e che in media ogni persona ha un testicolo.
Questo perché la media è solo un numero e nel caso di un campione poco omogeneo può somigliare poco all’esperienza dei più, rischiando di risultare fuorviante data la sua tendenza a lasciarsi influenzare dai valori estremi. Ad esempio, se nel campione che intervisto per un’indagine sul reddito dichiarato fosse incluso insieme a voi Bill Gates, la media non si avvicinerà più al vostro reddito. Questo perché la media è solo un indice di posizione, ovvero una delle diverse misure di tendenza centrale esistenti, e da sola non può bastare a rappresentare i dati, ma è necessario accompagnarla almeno con un indice di dispersione, come la variabilità che ci dica quanto tale numero è rappresentativo.
Infatti, se la media della poesia di Trilussa è sempre di un pollo a testa, sia che anch’io lo mangi o che lui li mangi entrambi, con un semplice calcolo della varianza si scopre l’inganno. Infatti, la varianza che nel primo caso sarebbe nulla (indicando che ad entrambi è toccata la stessa quantità), nel secondo caso risulta maggiore di 0. Gli statistici conoscono bene l’importanza della variabilità, dato che la statistica senza questa non serve a nulla. Se ci pensate, sapere il numero di scarpe medio dell’uomo adulto non aiuterà i produttori a decidere la quantità di scarpe di ogni misura da fornire ai consumatori, in quanto la stessa misura non andrà mai bene per tutti, come ci ricordiamo ogni volta che su un aereo ci ritroviamo stipati nel nostro sedile.
Nel 1809 Carl Friedrich Gauss (lo scienziato che si poteva ammirare sulle banconote da 10 marchi tedeschi prima dell'avvento dell'euro) stava studiando gli errori di misura in astronomia e nei rilevamenti topografici, quando si accorse che incappava spesso in una strana curva a campana. Questa rappresenta la distribuzione delle frequenze più elevate per i valori centrali, mentre in corrispondenza di quelli più estremi tende progressivamente a diminuire. E tale curva può descrivere moltissimi fenomeni. Si tratta di una regolarità della natura veramente straordinaria e perciò fu battezzata col nome di “distribuzione Normale”, in quanto rappresentava la “norma” per qualsiasi distribuzione presente in natura. Oggi sappiamo come moltissime caratteristiche si distribuiscono secondo una curva a campana e possono essere quindi approssimate con la distribuzione Normale (detta anche “curva Gaussiana”). Ne sono degli esempi la temperatura corporea delle persone adulte, la dimensione dell’encefalo degli studenti universitari e il numero di setole sull’addome dei moscerini della frutta. Anche Francis Galton rimase affascinato dal fatto che tale distribuzione, all’epoca detta Legge della frequenza degli errori, emergesse sistematicamente da situazioni di caos apparente. Ne scrisse:
«Non conosco niente che possa colpire l’immaginazione quanto la forma meravigliosa di ordine cosmico espressa dalla “Legge della frequenza degli errori”. Se i greci avessero conosciuto questa legge, l’avrebbero personificata e divinizzata. Essa regna in serenità e totale modestia, tra la confusione più selvaggia. Maggiore è la folla e l’apparente anarchia, più perfetto è il suo dominio. È la suprema legge dell’Irragionevolezza. Ogni volta che si richiama all’ordine un grande campione di elementi caotici e li si inquadra secondo le loro dimensioni, si scopre che una forma insospettata e meravigliosa di regolarità era presente da sempre.»
Archie Cochrane era un medico, epidemiologo e attivista che nel 1941, mentre era prigioniero di guerra nelle mani dei tedeschi, decise di improvvisare uno studio clinico. Dato che molti dei prigionieri (lui incluso) erano malati e Cochrane sospettava che la causa fosse una carenza dell’alimentazione, mise a confronto l’effetto di diete diverse. Riuscì così ad appurare cosa mancava alla dieta dei prigionieri e a portare prove incontrovertibili al comandante capo. Così facendo i prigionieri ricevettero integratori vitaminici che salvarono la vita a molti di loro[33].
Nel 1979 Cochrane scrisse: «una grave carenza nella nostra professione è il fatto di non avere predisposto la realizzazione di un elenco critico, suddiviso per specialità e aggiornato periodicamente, di tutti gli studi clinici controllati e randomizzati.» Effettivamente, data la folta schiera di bias che – come abbiamo visto – possono compromettere gli studi, capite come questi – se presi singolarmente – siano troppo vulnerabili per essere ritenuti attendibili. Infatti, molto raramente un singolo studio clinico ben condotto e ben scritto fornisce prove solide sugli effetti di un trattamento, anche soltanto per un problema di generalizzabilità dei risultati. Inoltre, se si confrontano ad esempio due trattamenti, eventuali differenze potrebbero essere dovute al caso, ma un campione non sufficientemente grande potrebbe non evidenziarlo.
Dopo la morte di Cochrane, Iain Chalmers portò avanti la sua battaglia, riuscendo a dare luce a un gruppo di ricercatori provenienti da tutto il mondo impegnati a revisionare, valutare, riassumere e pubblicare i migliori dati disponibili su un’ampia gamma di studi clinici: la Cochrane Collaboration. Sul sito della Cochrane oggi si possono trovare descrizioni sintetiche e chiare dello stato dell’arte in varie aree cliniche. Un gruppo che si prefigge il medesimo obiettivo per quanto riguarda le scienze sociali è la Campbell Collaboration. Ecco che così, verso la fine del 20° secolo abbiamo iniziato ad accettare l’idea che l’analisi di analisi provenienti da studi simili (ovvero la meta-analisi) e la valutazione critica e la sintesi di tutti gli studi rilevanti su un argomento specifico (ovvero le revisioni sistematiche) fossero strumenti importanti per evitare di trarre conclusioni errate. Un singolo studio sulle statine può dirci che il farmaco ha funzionato per un certo gruppo in un certo luogo, ma occorrono vari studi per corroborare il risultato riscontrato. Perciò si svolgono rassegne sistematiche e meta-analisi che includono tutti gli studi simili svolti sul tema, così che sia possibile – combinando i loro dati o i loro risultati – prendere una decisione razionale in merito.
La prima meta-analisi fu pubblicata da Karl Pearson nel 1904 e da allora il numero di revisioni sistematiche e meta-analisi pubblicate è aumentato rapidamente. Ad esempio, dagli anni ’50 agli anni ’90 più di centomila neonati sono morti in culla (SIDS). Il pediatra Benjamin Spock in quel periodo vendette 50 milioni di copie del suo libro intitolato Baby and Child Care, nel quale scriveva: «Penso che sia preferibile abituare un bambino a dormire a pancia in giù fin dall’inizio, se vuole» e con lui altri colleghi formularono raccomandazioni simili. Ma all’inizio degli anni Novanta alcuni ricercatori si resero conto che il rischio di SIDS si dimezzava se i bambini venivano addormentati sulla schiena, invece che a faccia in giù, e le successive campagne educative riuscirono a portare a un drastico calo del numero di decessi per morte in culla. Tuttavia, erano disponibili già dal 1970 ricerche che mostravano come dormire a pancia in giù fosse pericoloso per i neonati. Perciò una sintesi anticipata dei dati avrebbe potuto salvare molte vite.
Consultando i riassunti che Cochrane mette a disposizione mi è sorto un dubbio. Così ho provato a googlare “lo yoga cura l’incontinenza?” e tutti i primi risultati annunciavano che secondo la scienza c’erano prove sufficienti in questo senso, cantando le lodi dello yoga. Per capire davvero le cose sono dovuta tornare sul sito della Cochrane, dove si concludeva invece che: «Abbiamo identificato pochi studi sullo yoga per l’incontinenza e gli studi esistenti erano piccoli e ad alto rischio di bias. [...] A causa della mancanza di prove per rispondere alla domanda, non siamo sicuri che lo yoga sia utile per le donne con incontinenza urinaria. Sono necessari ulteriori studi ben condotti con campioni di dimensioni maggiori.» In questo caso la disinformazione non avrebbe fatto grandi danni, al massimo avremmo fatto un po’ di yoga, ma se la disinformazione toccasse aspetti vitali? In questo caso il risultato potrebbe rivelarsi fatale.
Le meta-analisi ci permettono quindi di generalizzare i risultati, consentendoci di determinare l’importanza e la coerenza degli effetti su una varietà di sistemi. Talvolta revisioni sistematiche e meta-analisi mostrano che non esistono ancora prove affidabili, altre volte confermano come l’evidenza attendibile proviene da un solo studio, ma anche questi sono risultati importanti da evidenziare. Oggi la maggiore disponibilità di questi "riassunti di dati" sta migliorando la qualità delle informazioni, ma comunque neanche questi devono essere accettati acriticamente, in quanto a loro volta sono frutto di scelte umane e quindi vulnerabili ai bias. Infatti, diverse revisioni che affrontano lo stesso quesito a volte arrivano a conclusioni diverse, dato che i loro autori possono selezionare, analizzare e presentare prove in modi che supportano i loro pregiudizi e interessi. Ad esempio, nel libro Come vivere più a lungo e sentirsi meglio, Linus Pauling (l’unica persona al mondo che ha ricevuto due premi Nobel non in condivisione) ha citato ben trenta studi a sostegno della sua idea che grandi dosi giornaliere di vitamina C riducono il rischio di contrarre il comune raffreddore, ma non ne ha nominato nemmeno uno contrario all’idea, anche se ne erano disponibili un gran numero.
Lo statistico britannico David John Hand ha scritto: «Come i telescopi, i microscopi, i raggi X e i radar, la Statistica moderna consente di vedere cose invisibili a occhio nudo». Ciò è vero, com’è vero che se uno davanti a un telescopio chiude gli occhi non vedrà mai nulla.
Dal momento che in statistica si cerca di rispondere a quesiti sulla popolazione generale a partire da un campione necessariamente ristretto, la stima che ne deriverà dovrebbe essere abbastanza umile da accompagnarsi a una stima dell’eventuale errore commesso nel processo di inferenza. Ecco perché uno statistico non si fiderebbe mai di una stima “puntuale”, ovvero così ingenua da viaggiare sola, senza un “intervallo di confidenza”, ovvero senza un intervallo di valori che, con un dato grado di fiducia, conterrà il vero parametro stimato. Un po’ come quando, prima di partire per una gita fuori porta, non guardiamo alla temperatura attesa a mezzogiorno per organizzare la valigia, ma ci informeremo piuttosto sulla temperatura minima e massima, perché le riteniamo stime più importanti.
Ovviamente l’intervallo di confidenza sarà più ampio al diminuire del grado di sicurezza impostato (più voglio essere certo che questo comprenda il valore reale, più ampio sarà l’insieme delle possibili stime), al crescere della variabilità del fenomeno studiato (se un fenomeno è ben definibile sarà più facilmente individuabile) e al diminuire della grandezza del campione (più grande è la proporzione di popolazione intervistata, più informazioni avrò sul valore reale). Il calcolo dell’intervallo di confidenza si basa sull’errore standard, che altro non è che un indice di variabilità che sarà tanto più piccolo quanto più attendibile sarà la stima a lui associata. Questo ragionamento fa parte dei fondamentali della cosiddetta statistica inferenziale, ma a quanto pare non è noto a tutti coloro che ci forniscono i dati.
Ad esempio, nel 2018 il sito BBC News annunciò che sul finire dell'anno precedente i disoccupati in Gran Bretagna erano diminuiti di 3000 unità e che in quel momento erano stimati pari a 1.44 milioni. Dimenticando di menzionare il fatto che questa stima, basata su un sondaggio svolto su 100 mila persone, aveva un margine d'errore di 77 mila unità, il che significa che il dato reale della disoccupazione poteva vedere, rispetto all’anno precedente, un aumento di 80 mila o una diminuzione di 3 disoccupati.
Attualmente i dati sono fra i beni che valgono di più sul mercato, poiché permettono alle aziende di conoscere le nostre abitudini, i nostri gusti e di tracciare il nostro profilo così da consigliare a potenziali futuri clienti i prodotti che si addicono di più ai loro gusti. I nostri dati nelle mani di Amazon, Apple, Facebook, Google e Microsoft rappresentano una vera e propria miniera d’oro. Ad esempio, Netflix e Amazon Prime hanno i dati su cosa guardiamo, quando lo guardiamo e possono sapere addirittura se abbiamo interrotto la visione; tali dati possono essere analizzati, incrociati e talvolta condivisi con altre aziende che li rivenderanno. Ogni volta che facciamo una ricerca su Google, o effettuiamo un pagamento online, twittiamo o regoliamo la temperatura di casa col termostato smart produciamo dati che solitamente servono a fornirci un servizio più personalizzato e quindi fatto ad hoc per noi. Le carte fedeltà che avete nel portafoglio ne sono un altro esempio. Invece di essere semplicemente un modo per usufruire di sconti al raggiungimento di una determinata spesa, per gli esperti di marketing rappresentano la chiave per capire i vostri gusti e tentare di fidelizzarvi. Senza la promessa dei punti, i clienti non avrebbero nessun motivo per usare una carta e rendersi riconoscibili ogni volta che fanno la spesa.
Il giornalista americano Charles Duhigg[34] ha raccontato in un articolo sul New York Times la storia emblematica di un uomo infuriato che andò a lamentarsi col responsabile di “Target”, uno dei più popolari grandi magazzini statunitensi, del fatto che sua figlia adolescente avesse ricevuto dei coupon per l’acquisto di vestiti per neonati e premaman. Il responsabile si scusò e, quando a qualche giorno dall’evento volle richiamare l’uomo, si sentì porgere delle scuse, in quanto il cliente aveva scoperto che sarebbe presto diventato nonno. Ecco il potere degli algoritmi! Infatti, da un acquisto insolito della ragazza, come ad esempio degli integratori di acido folico specifici per donne incinte, per l’algoritmo di Target – che aveva accesso a questa informazione – sarebbe stato molto semplice prevedere un inizio di gravidanza. Ma siccome da grandi poteri derivano grandi responsabilità, talvolta chi possiede i nostri dati ci invia – oltre ai coupon con sconti personalizzati – anche coupon casuali, proprio per non far trapelare che l’azienda ci conosca meglio di quanto crediamo[35]. Insomma, è proprio vero che nessuno fa niente per niente. Basta esserne consapevoli.
Siamo tutti portati a pensare che le coincidenze che sperimentiamo nella vita possano essere segni del destino. Le coincidenze ci affascinano e ci piace dare significati a eventi tanto improbabili da sembrarci assurdi. Senza sapere che la maggior parte delle coincidenze della nostra vita – come ad esempio incappare nel nostro vicino di casa mentre ci troviamo dall’altra parte del mondo, conoscere una persona con la quale condividiamo lo stesso compleanno oppure sognare un evento prima che questo si verifichi – possono essere spiegate con semplici considerazioni matematiche. Se ci sembrano così sorprendenti è perché non conosciamo le leggi di probabilità.
Un esempio noto risale ai primi anni Settanta, quando l’attore Anthony Hopkins venne ingaggiato per interpretare una parte nel film La ragazza di via Petrovka. Dopo aver cercato, senza successo, in diverse librerie il romanzo da cui il film è tratto, decise di rincasare, quando notò su una panchina della metropolitana una copia del libro che stava cercando. E, come se ciò non bastasse, scoprì poi che si trattava proprio della copia che l’autore del romanzo aveva perduto tempo addietro. Qual è la probabilità che un evento del genere accada? Uno su un milione? Uno su un miliardo? Mazur[36] l’ha calcolata e la probabilità che a qualcuno accada qualcosa di simile è prossima a quella di ottenere una scala reale a poker. Quindi difficile sì, ma non impossibile. Questo perché le coincidenze sono inevitabili, dato che anche ciò che è straordinariamente improbabile qualche volta dovrà pur accadere.
Un altro esempio di coincidenza apparentemente incredibile è quella avvenuta nella famiglia inglese Allali, in cui tutti e tre i figli sono nati lo stesso giorno in anni diversi. Il Daily Mail ha riportato la notizia affermando che si tratterebbe di un evento che capita una sola volta su 48 milioni, numero ottenuto moltiplicando tre eventi con probabilità di uno su 36.536. Ma – assumendo che la famiglia Allali non stesse cercando di seguire un piano familiare incredibilmente meticoloso, che non esistano anni bisestili (per praticità) e che un bambino abbia la stessa probabilità di nascere in ogni giorno dell’anno – dato che il primo figlio avrebbe potuto nascere in qualsiasi giorno, non dovrebbe comparire nella formula. Perciò, moltiplicando le probabilità di due eventi ciascuno pari ad uno su 365[37], risulta una probabilità di uno su 133 mila. Ciò fa di questo evento un caso raro, ma siccome in UK esistono circa 1 milione di famiglie con tre figli, ci dovremmo aspettare circa 7 casi di questo tipo all’anno. Capite quindi perché ciò che ci sembra impossibile, in realtà non lo è?
Il paradosso del compleanno è un classico esempio di questo tipo. Tale paradosso dimostra come bastino solamente 23 persone per rendere più probabile che improbabile il fatto che due fra queste spengano le candeline lo stesso giorno. In realtà, per quanto sembri incredibile, con sole 57 persone ne saremmo praticamente certi. Assurdo, vero? Eppure, se ci riflettiamo, 66 milioni di anni fa una cometa si schiantò vicino alla penisola dello Yucatan e quell’esplosione fu probabilmente responsabile dell’estinzione dei dinosauri e quindi, a catena, dell’evoluzione delle specie rimanenti e dell’avvento degli esseri umani. E se l’orbita di quella cometa si fosse trovata appena un chilometro più in là? Un chilometro non è nulla in scala astronomica, eppure sarebbe stato sufficiente a non far estinguere i dinosauri. Ecco perciò che gli umani sono figli di una coincidenza e l’importante è saperlo per continuare ad esserne affascinati, ma non sopraffatti.
Detto ciò, nemmeno gli statistici sono immuni dagli errori. Lo hanno dimostrato lo psicologo premio Nobel Daniel Kahneman e il suo collega Amos Tversky[38] ponendo ad alcuni ricercatori in psicologia domande statistiche non formulate in modo formale, tipo questa: supponete di vivere in una città in cui vi siano due ospedali, uno grande e uno piccolo. In un dato giorno, il 60% di bambini nati in uno dei due ospedali è maschio. Di quale dei due ospedali è più probabile che si tratti? Dato che i campioni più sono grandi, più tendono a fornire stime che si discostano poco dalla media reale, e dato che in media nascono 101 maschi ogni 100 femmine, la risposta corretta è l'ospedale più piccolo. Ma la maggior parte dei ricercatori non ci pensò e sbagliò.
Ma l’esempio madre di scivolone statistico ci è fornito da Sir Ronald Fisher, la figura più importante nella storia della statistica. Considerato uno dei grandi geni del secolo scorso, a lui dobbiamo anche la genetica teorica delle popolazioni, ma nessuno è perfetto, si sa. Infatti Fisher era anche un accanito fumatore e mentre era consulente scientifico del Tobacco Manufacturers’ Standing Committee si disse convinto che «La teoria che il cancro al polmone è causato dal fumo verrà alla fine considerata un grandissimo, catastrofico errore[39]». Lo studioso aveva avanzato infatti l’ipotesi secondo la quale sarebbe esistita una particolare predisposizione genetica che incide sia sulla comparsa delle malattie legate al fumo che sull’abitudine a fumare. La statistica, che rimane il miglior antidoto contro il pregiudizio, lo ha nel frattempo smentito. Perché apprendendo la statistica si prova la stessa sensazione che sperimentano i miopi indossando gli occhiali: tutto diventa improvvisamente più nitido.
«Dr Manhattan: – Eppure durante ogni accoppiamento umano migliaia di milioni di spermatozoi lottano per lo stesso uovo. Moltiplica queste probabilità contrarie per generazioni. Contro le probabilità che i tuoi antenati siano vivi, che si incontrino, che generino precisamente quel figlio, esattamente quella figlia... Fino a quando tua madre ama un uomo che ha tutte le ragioni per odiare e da quell’unione fra milioni di bambini potenziali in competizione sei stata tu, e solo tu, a emergere. Distillare una forma così specifica da un simile caos di improbabilità è come trasformare l’aria in oro... È l’improbabilità suprema.
Laurie: – Potresti dire lo stesso di chiunque altro al mondo!
Dr Manhattan: – Sì, chiunque altro. Ma il mondo è così affollato di persone, così affollato di persone, così affollato di questi miracoli, che diventano comuni e ce ne dimentichiamo!»
Watchmen, Alan Moore
Nessuno è perfetto, dicevamo, nemmeno l'Agenzia Italiana del Farmaco. Che nel Rapporto Annuale sulla Sicurezza dei Vaccini COVID-19 ha clamorosamente sbagliato l’analisi del confronto fra decessi osservati e attesi nei 14 giorni successivi alla somministrazione del vaccino anti Covid (pagine 24-26)[40]. Nonostante la statistica fosse sbagliata, la conclusione presentata era giusta e mostrava che non esiste un'associazione tra la somministrazione del vaccino e il numero di decessi nelle settimane successive. In ogni caso, si è trattato di un errore grave.
Vediamo quel che è successo. Sono stati confrontati i decessi previsti (attesi) per fasce d'età in un periodo di due settimane con quelli osservati nei quattordici giorni successivi alla somministrazione del vaccino. «L’analisi osservati-attesi (analisi O/A) ha lo scopo di confrontare il numero di eventi che si sono effettivamente verificati in una popolazione esposta a un ipotetico fattore di rischio (casi 'osservati’), con il numero di eventi che si sarebbero verificati in condizioni naturali in assenza del fattore di rischio (casi 'attesi’)», scrivono. L’ipotetico fattore di rischio è il vaccino, la popolazione esposta sono tutti i vaccinati.
L’AIFA stima i casi attesi, ovvero il numero di decessi che ci saremmo aspettati in quella stessa popolazione di soggetti in assenza di vaccinazioni, usando la probabilità di decesso osservata nel 2019 in un periodo di 14 giorni causata dalla normale mortalità (per vecchiaia, per incidenti, per malattie…). Ovviamente, dato che la mortalità è più bassa per i giovani e più alta per gli anziani, l’analisi è stata condotta per fasce di età. Queste poi sono state confrontate con quelle osservate nella realtà, ovvero dopo l’esposizione al vaccino. I casi osservati dovrebbero essere quindi tutti i decessi avvenuti entro 14 giorni dalla somministrazione del vaccino, ma invece di prendere tutte le morti avvenute dopo il vaccino per ogni causa, l’AIFA decide che «i casi osservati coincidono con tutte le segnalazioni ricevute nei 14 giorni successivi alla somministrazione dei vaccini anti-COVID-19». Ma fra tali segnalazioni non ci sono le morti da incidenti e tante altre cause fatali che invece vengono correttamente considerate nel calcolo delle morti attese. Questo equivale a confrontare un cesto di frutta con un altro, del quale però si considerano solo le banane. Così facendo, le morti osservate sono irrisorie rispetto alle morti attese. Ma anziché stupirsi del fatto che i due numeri, morti attese e morti osservate, che dovrebbero essere simili tra loro, siano in realtà così distanti, l’AIFA conclude che «i decessi osservati sono sempre nettamente inferiori ai decessi attesi e non c’è quindi, nella popolazione di soggetti vaccinati, alcun aumento del numero di eventi rispetto a quello che ci saremmo aspettati in una popolazione simile ma non vaccinata.» Così facendo avrebbero potuto paradossalmente dichiarare che il vaccino protegge anche da morte per incidente stradale!
Intervista a dott.ssa Rina Camporese, dott.ssa Patrizia Collesi, dott.ssa Susi Osti dell’ISTAT
In quali curriculum è inserito l'insegnamento della statistica e da quando?
L’insegnamento della statistica fin dai primi livelli di istruzione è fondamentale per garantire lo sviluppo e il sostegno della cultura “quantitativa” anche dei più piccoli. L’introduzione della statistica nei programmi di insegnamento della scuola di base italiana risale al 1979 per la scuola media (oggi scuola secondaria di primo grado) e al 1985 per la scuola elementare (oggi scuola primaria). Le indicazioni nazionali operano sull’intero territorio nazionale.
Si insegna la teoria metodologica o la lettura dei dati?
L'insegnamento prevede competenze e abilità in statistica, come padroneggiare gli strumenti (grafici e tabelle) per leggere e interpretare l’informazione quantitativa a partire dal primo ciclo di istruzione fino a tutto il secondo ciclo. Nei programmi di matematica prevale l’insegnamento delle tecniche di elaborazione dei dati con strumenti matematici; mentre i libri di testo di molte altre discipline presentano dati da “leggere” (l’esempio principale è la geografia).
Com'è recepito tale insegnamento?
Non possiamo esprimere una valutazione su come sia percepita in generale la presenza della statistica nei programmi scolastici. Ma possiamo testimoniare che le numerose iniziative Istat per insegnanti e allievi trovano sempre un'ottima accoglienza da parte delle scuole. Ogni anno sono centinaia le scuole con cui collaboriamo e migliaia le persone giovani che “sperimentano” la statistica in classe insieme all’Istat: testimoniano soddisfazione e desiderio di approfondire.
Le Olimpiadi di Statistica quando sono state lanciate? Quante persone partecipano?
Nell’anno scolastico 2021-22 si è svolta la XII edizione delle Olimpiadi della Statistica. Queste, essendo rivolte alle studentesse e agli studenti delle superiori, garantiscono a chi vince la fase individuale l'iscrizione all'Albo nazionale delle Eccellenze, che è un bel premio di per sé, perché le Università abbonano le tasse di iscrizione. La fase a squadre permette invece a chi vince di partecipare alle Olimpiadi europee, decisamente più orientate alla conoscenza dei dati di statistica ufficiale prodotti dai vari Istituti nazionali di statistica e da Eurostat, che non alla parte teorica. Alle Olimpiadi europee partecipano 17 Paesi. Quest’anno su un totale (ancora non definitivo) di 16.507 iscritti complessivi, la quota proveniente dall’Italia è di 5.195 persone. Quelle effettivamente partecipanti sono state poi 4.172, per un totale di 135 scuole in tutto il territorio nazionale. Negli ultimi anni abbiamo riscontrato una notevole crescita dei licei partecipanti.
Ma, anche senza bisogno di addentrarci tanto, la statistica può aiutare ognuno di noi in svariate situazioni, tanto che la Divisione Statistica delle Nazioni Unite descrive il ruolo delle statistiche ufficiali come «elemento indispensabile nel sistema informativo di una società democratica». Anche l’ex presidente INPS, Tito Boeri, ha definito la statistica una «sentinella della democrazia». Ed è veramente così.
«Le informazioni statistiche riguardano la trasparenza: quando conosci la reale situazione del tuo Paese puoi chiederne conto al governo. I dati sono padre e madre per la democrazia», puntualizza Albina Chuwa, direttore generale dell’Ufficio di statistica nazionale della Tanzania[1].
Gli analisti hanno osservato che «di per sé le statistiche non portano benefici, ma è l’uso delle statistiche che offre vantaggi, permettendo al governo, alle aziende, alle organizzazioni non governative e ai singoli individui di prendere decisioni migliori e in tempi più rapidi[2]». Quando giornalisti, opinionisti o studiosi vogliono sapere cosa succede nel Paese si basano sempre sulle statistiche ufficiali. La Metropolitan Police di Londra, ad esempio, usa il censimento per individuare le strade dove vivono più cittadini anziani in modo da concentrare lì gli sforzi delle squadre incaricate di prevenire truffe e furti ai danni delle persone più vulnerabili. La Nuova Zelanda ha dimostrato come i dati forniti dal censimento permettano di allocare in maniera più efficiente le risorse per sanità e trasporti e in generale consentano politiche meglio calibrate[3].
E le statistiche ufficiali sono a disposizione di ognuno di noi e sono gratuite. Basandosi su queste, lo storico Du Bois e il suo team realizzarono grafici magnifici che mostrarono all’Exposition Universelle del 1900 a Parigi, al fine di denunciare la drammatica situazione degli afroamericani negli Stati Uniti dell’epoca[4]. Un ottimo esempio di come saper maneggiare i dati possa servire a comprendere il mondo e, possibilmente, a migliorarlo.
Com’è quindi possibile che – in un periodo storico in cui si parla di sovraccarico informativo e di infodemia, in cui i dati sono resi pubblici e la stragrande maggioranza della popolazione è in grado di leggere e scrivere – esistano ancora persone che non si fidano dei risultati della statistica?
Secondo l’efficace sintesi di Gerd Gigerenzer: «Numbers are public, but the public is not generally numerate» (“I numeri sono pubblici, ma il pubblico generalmente non sa fare di conto”). Infatti, un motivo potrebbe essere la carenza di alfabetizzazione statistica (numeracy), dato che l’introduzione di questa materia nei curricula scolastici è piuttosto recente. Il nostro Paese non sembra essere cambiato molto da quando su la Repubblica leggevamo che «gli italiani, e in modo particolare i ragazzi, ignorano cosa faccia uno studioso di statistica. Per lo più, l’idea che hanno è quella di una specie di topo d’archivio che passa la sua vita a sbagliare sondaggi elettorali e a fare figuracce in tv»[5]. Inoltre, anche pratiche incoerenti, fonti dubbie e qualità dei dati eterogenea hanno contribuito a far vacillare la fiducia del pubblico nei dati.

Indice di errata percezione per Stato, IPSOS, “People in Italy and the US are most wrong on key facts about their society”, 30 agosto 2018, bit.ly/3OE755U
Che sia questo analfabetismo statistico la ragione per cui l’Italia risulta essere il Paese con la percezione più distorta della realtà in una classifica che confronta 13 nazioni occidentali[6]? Questo è il risultato di una ricerca che ha analizzato un campione di oltre 50 mila interviste realizzate negli ultimi cinque anni, e nella classifica siamo seguiti da Stati Uniti e Francia.
Dal numero di omicidi, fino all’incidenza del diabete e dell’immigrazione: «Ci sbagliamo quasi su tutto» scrive il direttore della sezione inglese dell’istituto di ricerca Ipsos, Bobby Duffy. L’Italia è per esempio il paese dell’Unione europea in cui c’è il maggiore divario tra gli immigrati “percepiti” e quelli realmente presenti sul territorio nazionale. Secondo quanto emerge dalla ricerca, la stragrande maggioranza dei cittadini italiani sovrastima la presenza di immigrati: a fronte di un 7% di stranieri presenti nel paese, gli italiani infatti ritengono che questi siano il 30%.
Perciò è fondamentale allenare la mentalità statistica, così da essere in grado di confrontare e analizzare informazioni significative in mezzo a un gran rumore di dati. Ecco quindi, nel caso ne sentiste il bisogno, qualche buon motivo per cui varrebbe la pena apprendere almeno le basi della statistica.
Indice |
Per non farsi ingannare da risultati contro-intuitivi
In questo periodo storico siamo particolarmente bombardati da dati che talvolta possono sembrarci imperscrutabili.
Consideriamo per esempio il risultato relativo ai decessi di persone positive alla variante Delta del Covid-19 in Inghilterra nel periodo tra il 21 giugno e il 12 settembre 2021: nella popolazione complessiva la percentuale dei non vaccinati morti era inferiore di circa 1.3 volte di quella dei vaccinati. Com’è possibile?
Tale fenomeno è spiegabile grazie al paradosso di Simpson, noto per essere la causa di molti errori di interpretazione. Secondo questo paradosso, quando si analizza una popolazione composta da diversi gruppi è possibile che all’interno di essi si evidenzi un fenomeno simile, mentre se guardiamo alla popolazione generale il fenomeno si capovolge, nel senso che emerge una relazione tra variabili opposta rispetto a quella reale.
Per esempio, se prendiamo in considerazione gli inglesi con meno di cinquant’anni scopriremo che la percentuale di decessi è inferiore nella popolazione vaccinata rispetto a quella non vaccinata. E lo stesso accade se analizziamo il sottogruppo degli inglesi sopra i cinquant’anni. Ma confrontare le percentuali nell’intera popolazione introduce una distorsione dovuta all’età e un modo per correggerla sarà quindi limitare il confronto per fasce d’età il più possibile omogenee per quanto riguarda il tasso di vaccinazione.
Un altro famoso esempio di questo paradosso è il caso dell’università di Berkeley, dove si osservò come il tasso di ammissione femminile fosse molto inferiore a quello maschile[7]. L’università avrebbe potuto venire accusata di discriminazione sessuale, quindi! Una più adeguata analisi dei dati mostrò che l’accusa era infondata: infatti, considerando i tassi di ammissione per dipartimento, la situazione era rovesciata, in quanto nella maggior parte dei dipartimenti le donne facevano registrare un tasso di ammissione più elevato. Magia? No, statistica.
A non dimenticare mai che tutto è relativo
Da due anni a questa parte siamo abituati a sentire i presentatori dei telegiornali dare letteralmente i numeri ogni giorno. Ma questi numeri snocciolati per regione, oltre a risvegliare in noi un forte senso di preoccupazione, hanno un senso? Spesso no.

Numero di nuovi positivi certificati il 1ˆ dicembre 2020 sul sito della Protezione Civile, riprodotta coi dati scaricabili da https://bit.ly/3yOZNGs
Il 1° dicembre 2020 la Lombardia era la regione con il maggior numero di nuovi casi di positivi al COVID-19, 4.048, seguita dal Veneto con 2.535 casi e dal Lazio con 1.669. Questa figura dà subito l’idea di come in Lombardia l’epidemia fosse molto più estesa rispetto alle altre regioni, mentre chi viveva in Friuli poteva stare tutto sommato tranquillo, essendo la regione posizionata verso metà classifica.
Ma la classifica risente della numerosità della popolazione nelle singole regioni, dato che a parità di diffusione del contagio una regione con il doppio degli abitanti rispetto a un’altra avrà anche il doppio di positivi. Ci sarà infatti una bella differenza tra avere duemila nuovi casi in Lombardia (che è la regione più popolosa d’Italia) o averli in Valle d’Aosta (che è invece l’ultima in classifica per quanto riguarda il numero di residenti). Non ha quindi alcun senso comunicare i numeri assoluti, mentre è molto più informativo fornire i numeri relativi, dividendo il numero di casi positivi per il numero degli abitanti.

Numero di nuovi positivi certificati il 1ˆ dicembre 2020 ogni 100.000 abitanti, riprodotto da: https://bit.ly/3zbsO0g.
Ed ecco che il quadro cambia notevolmente, con la Lombardia che scivola al 4° posto e il Friuli che schizza al 1°, per un’incidenza (numero di nuovi casi) doppia rispetto al Lazio, pur avendo la metà dei positivi in numeri assoluti. Attenzione quindi a chi vi propone numeri assoluti: o non sa cosa sta facendo, o sta cercando di manipolarvi.
A riconoscere la distorsione ed evitarla
Un mondo senza distorsioni sarebbe meraviglioso, ma purtroppo in quello in cui viviamo queste abbondano. La distorsione (o bias) è una modifica, intenzionale o meno, del disegno e/o della conduzione di uno studio, dell’analisi e della valutazione dei dati, in grado di incidere sui risultati, portando a conclusioni sistematicamente diverse dalla verità. E ce n’è veramente per tutti i gusti: dal bias di progettazione a quello di allocazione, passando per quello di pubblicazione e di analisi, o nella valutazione, di frode della ricerca, o il bias di presentazione selettiva (su cui vi segnalo un video di Monty Python che lo spiega in modo inconsapevolmente divertente[8]), ecc.
Un famoso esempio di distorsione campionaria si è verificato alle elezioni presidenziali statunitensi del '36, alle quali concorrevano il governatore del Kansas, Alfred Mossman Landon e il democratico Franklin Delano Roosevelt. In quel periodo l’autorevole settimanale Literary Digest organizzò un sondaggio che venne inviato per posta a 10 milioni di persone. Sulla base delle risposte pervenute, che erano 2.4 milioni, predisse una vittoria per 3 a 2 per il candidato repubblicano, mentre lo statistico George Gallup (che negli anni Trenta essenzialmente inventò i sondaggi di opinione) ottenne un risultato opposto su un campione estremamente più esiguo di votanti e finì per avere ragione.
Roosevelt, infatti, non solo vinse, ma lo fece in modo schiacciante. L’errore del giornale fu quello di costruire il campione usando gli elenchi degli abbonati telefonici e dei proprietari di automobili, all’epoca beni poco diffusi. Questo fece sì che il campione fosse per lo più composto da cittadini benestanti e ciò produsse inevitabilmente risultati distorti, dato che i sostenitori di Roosevelt provenivano più che altro dalle classi meno abbienti. Inoltre, tutte le persone che non hanno risposto al sondaggio della rivista costituiscono quello che lo statistico David Hand definisce dark data, dati oscuri: le risposte mancanti. Sappiamo che le persone esistono ma non è dato sapere cosa pensino: possiamo ignorarle o tentare di far luce su ciò che manca, ma probabilmente il problema rimarrà.
Per poter generalizzare dal campione alla popolazione è cruciale che il campione sia rappresentativo, più che grande. Avere tanti dati non garantisce necessariamente la bontà del campione. Ne è un ulteriore esempio la società di sondaggi che nel 2015 fallì miseramente nel tentativo di prevedere i risultati delle elezioni britanniche, nonostante avesse intervistato migliaia di elettori. Successivamente un’inchiesta svelò come nel sondaggio telefonico la maggior parte dei numeri chiamati corrispondesse a telefoni fissi e che aveva risposto meno del 10% delle persone chiamate. Ecco quindi che difficilmente un campionamento di questo tipo potrà risultare rappresentativo. Questo tipo di problema ha afflitto anche i sondaggi del 2016 che davano Hillary Clinton in vantaggio rispetto a Donald Trump negli stati decisivi.[9]
Gallup trovò una buona analogia per sottolineare l'importanza del campionamento casuale dicendo che quando cuciniamo la zuppa in un pentolone non è necessario mangiarla tutta per capire se manca il sale: se mescoliamo a dovere basterà assaggiarne una cucchiaiata.
L’idea dell’importanza di un buon mescolamento si concretizzò nel 1969 nella lotteria della leva per la guerra in Vietnam dove, in base a una lista ordinata di date di nascita, sarebbero partiti prima gli uomini corrispondenti alle date in cima alla lista. Per cercare di rendere equa la selezione decisero di estrarre casualmente le date di nascita da una scatola, ma questa non fu mescolata e chi estraeva non infilò la mano sino in fondo.[10] In questo modo furono sfavoriti i nati nella seconda parte dell’anno.
Ma gli errori di campionamento sono infidi e si nascondono dappertutto, anche in studi ambiziosi come quello svedese che seguì più di 4 milioni di cittadini per oltre diciotto anni e arrivò a concludere che gli uomini con uno status socioeconomico più elevato avevano un tasso leggermente maggiore di tumori cerebrali. La notizia si trasformò nell’inquietante titolo giornalistico: Perché andare all’università aumenta i rischi di tumore cerebrale.[11] Che forse le sgobbate in biblioteca provochino qualche surriscaldamento nel cervello degli studiosi? Direi piuttosto che le persone benestanti e più istruite si interfacciano con medici migliori che gli procureranno una diagnosi prima e verranno così inserite nel registro dei casi di cancro.
Un esempio divertente è quello dello studio[12],[13], che mostrava i risultati ottenuti analizzando le lesioni riportate da alcuni gatti precipitati dai grattacieli di New York. Osservando i risultati non sorprende vedere che i gatti caduti dal quinto piano riportino più lesioni rispetto a quelli precipitati dal secondo, e che a quelli caduti dal settimo o ottavo vada ancora peggio. Ciò che ci stupisce è che oltre a queste altezze le cose sembrano migliorare: il numero medio di lesioni si riduce nei gatti precipitati dal nono piano in poi, tanto da avvicinarsi a quello osservato in gatti caduti dal secondo piano. Incredibile, non è vero? Gli autori giustificano lo strano fenomeno spiegando che, dopo aver raggiunto la velocità limite di caduta, il gatto si rilasserebbe e così facendo ammortizzerebbe l'impatto col suolo.
La spiegazione in realtà è molto meno romantica, in quanto l’inghippo sta nella costruzione del campione che era basato sui registri veterinari. Infatti, se un gatto cadeva dal ventesimo piano probabilmente, invece di essere condotto da un veterinario, finiva direttamente nel più vicino cimitero per animali. In questo specifico esempio il campione soffriva del bias di sopravvivenza, che induce ad attribuire a un numero esiguo di “sopravvissuti” il privilegio di rappresentare il gruppo molto più ampio al quale apparteneva originariamente.
Un altro esempio di bias di sopravvivenza risale al 1943, quando le forze armate statunitensi chiesero al matematico Abraham Wald un parere su come rendere più robusti i loro aerei. Capitava che questi tornassero dalle missioni con la fusoliera e le ali sforacchiate dai proiettili, aveva senso corazzare queste parti, dato che sembravano le più vulnerabili? Secondo Wald non veramente, infatti lui si chiese piuttosto cosa si sapeva degli aerei che non rientravano. Dato che raramente si erano osservati aerei di ritorno con danni a motori e serbatoi, forse quelle erano proprio le parti più sensibili ai danni fatali. Ma era semplicemente impossibile osservarle danneggiate in quanto in quei casi l’aereo non aveva scampo e veniva abbattuto.
Lo stesso errore lo commetteremmo se, vedendo che tre dei cinque studenti con i migliori voti all’università provengono dallo stesso liceo, credessimo che quel liceo offra un’istruzione migliore degli altri, perché in realtà si potrebbe semplicemente trattare di una scuola molto grande. Per poter valutare in modo oggettivo dovremmo valutare anche i voti degli studenti non “sopravvissuti” al processo di selezione.
Questo pregiudizio inficia il ragionamento anche di quel ristoratore che decida di aprire un nuovo locale in una tale città, confortato dai numerosi ristoranti di successo che vi operano. Infatti, così facendo, sta ignorando la possibilità che quei ristoranti di successo rappresentino solo la parte “sopravvissuta” di un insieme molto più ampio. Magari il 90% dei ristoranti aveva fallito durante il primo anno ma di loro lui non sa nulla dato che, per dirlo con le parole del saggista Nassim Nicholas Taleb, “il cimitero dei ristoranti falliti è molto silenzioso”.[14]
A saper leggere i grafici
La specie umana è una “specie visiva”, il cui encefalo si è evoluto per elaborare le informazioni visive. Perciò l’occhio umano è per sua natura in grado di identificare in ciò che osserva andamenti regolari ed eccezioni ai pattern. Inoltre i numeri non parlano per sé ma sta a noi dar loro un significato. Ecco quindi perché al giorno d’oggi le rappresentazioni grafiche possono insinuarsi ovunque.
Ma due secoli fa, quando nacque Florence Nightingale, non era certamente così. Questa infermiera inglese allo scoppiare della guerra di Crimea fu inviata a dirigere una squadra di colleghe in un ospedale di Istanbul che versava in pessime condizioni. Florence, oltre a riorganizzare l’ospedale, iniziò ad annotare meticolosamente ogni dato rilevante a sua disposizione. Una volta rientrata in Inghilterra si rese conto dell’importanza di quei dati per comprendere meglio il problema e studiare delle soluzioni a riguardo. Serviva però un metodo per riassumere i principali problemi rilevati (come le infezioni, la malnutrizione e la mancanza di igiene) che non fosse la mera costruzione di noiose tabelle, spesso incomprensibili. Fu così che si inventò una sorta di istogramma circolare (diagramma della rosa) nel quale riuscì a sintetizzare le circa mille pagine di dati raccolti. Questi evidenziarono come la principale causa di morte dei soldati durante la guerra non fossero le ferite, bensì le malattie.
Lei, anche se incredula, richiese l’invio di una squadra di supporto per ripulire l’ospedale e nel 1877 arrivò dal Regno Unito una commissione sanitaria incaricata di dipingere le pareti, di rimuovere lo sporco e gli animali morti e di spurgare le fogne. Dopo il suo intervento sull’igiene in quell’ospedale la mortalità scese dal 42 al 2%.
Lei fu una delle prime persone al mondo a capire come un diagramma suscitasse reazioni molto più intense rispetto a una tabella piena di numeri e che una rappresentazione grafica, se ben pensata e organizzata, fa trapelare subito messaggi che dei semplici valori numerici non sono in grado di mostrare. Col passare del tempo, anche i medici fecero proprie le argomentazioni di Florence e attuarono dei provvedimenti in materia di igiene. Questa iniziativa si estese gradualmente fino a quando negli anni Settanta dell’Ottocento il parlamento approvò svariate leggi per promuovere la salute pubblica e la mortalità nel Regno Unito iniziò a calare, mentre parallelamente l’aspettativa di vita aumentò.
Fu così che Florence divenne la prima donna raffigurata su una banconota britannica, a parte la Regina. Per far fronte alla pandemia COVID-19, a Londra fu costruito un ospedale che porta il nome “Nightingale Hospital” in suo onore. La rivista Big Issue le ha dedicato la copertina del numero di marzo 2020 con un titolo che la acclamava per aver insegnato al mondo intero l’importanza di lavarsi le mani: un gesto che oggi riteniamo scontato, ma che non lo era affatto all’epoca, e che è stato anche il gesto fondamentale per combattere la pandemia in corso. Della grande Florence Nightingale dissero:
«Florence Nightingale credeva – e in tutte le azioni della sua vita agì con quella credenza – che l’amministratore può avere successo solo se guidato dalla conoscenza statistica. Il legislatore – per dire nulla del politico – sbagliava troppo spesso per la mancanza di questa conoscenza. No, lei è andata oltre; riteneva che tutto l’universo – comprese le comunità umane – si stava evolvendo secondo un piano divino; che lo scopo dell’uomo era sforzarsi di comprendere questo piano e guidare le proprie azioni in accordo con esso. Ma per comprendere i pensieri di Dio lei riteneva che dobbiamo studiare statistica, perché è quella la misura del Suo scopo. Quindi lo studio della statistica era per lei un dovere religioso.»[15]
Noi statistici la ricordiamo per aver dimostrato l’efficacia dei dati e averci aperto un nuovo canale di comunicazione complesso quanto utile. Nell’introduzione al suo libro Envisioning Information, l’information designer Edward Tufte ci mette in guardia: «I grafici richiedono una lettura attenta. Sono veri e propri scrigni traboccanti di significati, ma sono anche complessi e arguti». Perciò chiediamoci sempre quali, tra i mille grafici che ci bombardano ogni giorno, sono realmente attendibili e non manipolatori. Solitamente sono di contorno e tendono a distrarci, anche perché spesso vengono affidati al reparto grafico, con solida formazione artistica ma carente in quanto a competenze statistiche, mentre, come spiega il professor Alberto Cairo, «un buon grafico non è un’illustrazione bensì una spiegazione visiva».[16]
Un esempio particolarmente attuale di cattiva rappresentazione grafica è comparso nel tweet di una (sedicente) biologa molecolare dove sono disegnate due curve simili che rappresenterebbero i numeri di positivi tra vaccinati e non (per milione, fascia di età 40-59) per settimana nel periodo dal 14 luglio al 27 ottobre 2021.
Tale grafico veniva esibito allo scopo di dimostrare che il vaccino non servirebbe a proteggere dal contagio nella pandemia del COVID-19, dato che i positivi aumenterebbero in entrambi i gruppi e il trend sarebbe simile. Effettivamente le curve dei contagi sono altamente correlate, dato che se crescono i positivi tra i no-vax aumenteranno anche quelli tra i vaccinati, trattandosi di una malattia infettiva. Peccato però che la scala usata a destra per i no-vax era circa cinque volte quella usata a sinistra per i vaccinati. Saper leggere i grafici protegge anche da questi vecchi trucchetti ben noti a noi statistici.
Perché un soldo risparmiato è un soldo guadagnato
Un sintomo della scarsa alfabetizzazione statistica nel nostro Paese è rappresentato – a mio avviso – dalla permanenza sui principali siti del lotto italiani[17],[18], degli elenchi dei cosiddetti “numeri ritardatari”, ovvero di quei numeri che non escono da diverse estrazioni. Secondo i sostenitori di questo metodo, la Legge dei grandi numeri assicurerebbe che a lungo termine ogni cifra verrà estratta con una frequenza pressappoco uguale, perciò quelli ritardatari dovranno necessariamente uscire più frequentemente in modo da recuperare la 'timidezza’ iniziale. Se così fosse, puntando su questi numeri timidi si avrebbe una maggiore probabilità di vincere.
Questa teoria avvincente non tiene purtroppo in considerazione il fatto che ogni estrazione è indipendente dalle precedenti, perciò ogni volta tutti i numeri avranno sempre la stessa probabilità di uscire, esattamente come ad ogni lancio di moneta si avrà sempre la stessa possibilità che esca testa o croce anche al secondo lancio, indipendentemente dal risultato appena ottenuto. Esattamente come il fatto di essere già sopravvissuti a un incidente aereo non ci potrà proteggere dall’infausto evento di ritrovarci nuovamente protagonisti di un altro incidente aereo. In statistichese diciamo che «l’urna non ha memoria».
La teoria dei numeri ritardatari, infatti, confonde la frequenza assoluta di un dato numero (cioè il numero di volte che questo è stato estratto) con la frequenza relativa (ovvero il rapporto tra le estrazioni di un numero e tutte le estrazioni). Soltanto quest’ultima è soggetta alla Legge dei grandi numeri e tende a bilanciarsi per ogni cifra, mentre le frequenze assolute (che sono quelle effettivamente pagate dal banco) possono anche divergere. Ad esempio, se dopo 100 lanci di una moneta sono uscite 40 teste e 60 croci, la teoria dei ritardi suggerisce di puntare sulle teste. Ma se dopo altri 900 lanci la situazione sarà di 450 teste e 550 croci, le frequenze relative si saranno avvicinate (proprio come stipulato dalla Legge dei grandi numeri) ma nei lanci supplementari il numero di croci uscite è stato ancora superiore.
Se oggi abbiamo queste conoscenze lo dobbiamo al cavaliere de Méré, giocatore accanito grazie ai cui dubbi nacque il Calcolo delle probabilità, disciplina che indica come l’unico modo per non perdere sia, semplicemente, non giocare.
Per sapere cosa si intende veramente con Legge dei grandi numeri
Da uno studio sull’incidenza del cancro ai reni nelle 3141 contee statunitensi è emerso che quelle con l’incidenza di questa malattia più bassa erano per lo più rurali, poco popolate e situate in Stati tradizionalmente repubblicani del Midwest, del Sud e dell’Ovest. Come ve lo spiegate? Immagino abbiate escluso che la politica repubblicana sia una cura preventiva del cancro ai reni, più probabilmente sarete giunti anche voi alla conclusione plausibile che queste percentuali così basse siano dovute alla vita sana delle comunità rurali, dove l’inquinamento è sensibilmente minore e si ha accesso a cibi freschi e senza additivi.[19]
E se vi dicessi che le contee con un'incidenza più alta di questa malattia sono per lo più rurali, poco popolate e situate in Stati tradizionalmente repubblicani del Midwest, del Sud e dell’Ovest? Potrebbe essere causato dallo scarso accesso alle cure mediche, dall’alimentazione ricca di grassi e dal troppo consumo di alcol e tabacco? Ma com’è possibile che lo stile di vita rurale incida sia sull’alta che sulla bassa incidenza del cancro ai reni?
Si spiega con la spesso citata, purtroppo come abbiamo già visto a sproposito, Legge dei grandi numeri. L’abbiamo appena visto con i numeri del lotto, ma altri esempi potrebbero essere presi dal bar più vicino a casa, come: «Ieri c’è stato un incidente sulla tangenziale est, quindi per la legge dei grandi numeri è praticamente impossibile che se ne verifichi un altro» oppure «Il Parma ha vinto nove partite consecutive, quindi per la legge dei grandi numeri è altamente probabile che questa domenica perda». Tutto ciò non ha nulla a che vedere con questa povera legge, in quanto non esiste nessuna oscura tendenza compensatrice che spinga gli eventi in una direzione opposta a quella nella quale sono andati fino ad ora i fatti.
La legge dei grandi numeri afferma solo che, ad esempio, se peschiamo molte volte una carta da un mazzo, la probabilità di trovare proprio una certa carta (target) tende a coincidere col numero di carte uguali al target diviso per il numero totale di carte. In altre parole: i campioni più grandi forniscono stime più precise. Nella pratica, se volessimo una stima affidabile dell’altezza, tale legge suggerisce di misurare più persone possibili. La legge dell’acqua calda, non è vero?
Ecco perciò che se due persone si mettessero a prelevare biglie dallo stesso vaso che ne contiene sia rosse che bianche, ma una ne estraesse sempre quattro e l’altra sette per un numero di volte sufficientemente lungo, le estrazioni estreme (ovvero tutte bianche o tutte rosse) saranno molto più frequenti nei campioni da quattro, rispetto a quelli da sette. Quindi, se la popolazione statunitense fosse il vaso nel quale abbiamo città e contee e alcune biglie fossero contrassegnate dal cancro ai reni, invece che da un colore, i campioni rurali, più piccoli degli altri, sono più probabilmente soggetti a risultati estremi (incidenza molto elevata o molto bassa di tal cancro) rispetto ai campioni più grandi. Ecco quindi perché i risultati su campioni grandi sono più attendibili di quelli su campioni piccoli.
Per riconoscere relazioni insignificanti
Esiste un numero che è in grado di misurare quanto due variabili si comportino nello stesso modo: si tratta del coefficiente di correlazione. La correlazione misura l’associazione tra due caratteristiche. Banalmente l’altezza correla col peso, dato che le persone più alte tendono generalmente a pesare di più. I nostri antenati, ad esempio, notarono che masticare la corteccia di salice alleviava i disturbi nelle persone che soffrivano di cefalea e di febbre. Da questa osservazione è nata l’invenzione dell'aspirina. Le correlazioni sono perciò indici potenti della possibile esistenza di una relazione causa-effetto.
Una pubblicazione su una rivista scientifica,[20] ad esempio, rivelava che le cicogne portano i bambini sulla base della correlazione tra numero di nati e numero di cicogne nei paesi europei. Ma sarà veramente così? Favole e leggende identificano la cicogna come animale beneaugurante, portatore di fecondità, ma si basano su un piccolo equivoco. Infatti, una volta, quando nasceva un bambino, in casa si accendeva il camino per più ore durante la giornata per scaldare l’ambiente. Se questo accadeva in primavera, le cicogne di ritorno dall’Africa, cercando il luogo più adatto per nidificare, optavano per il comignolo più caldo e quindi per quello della casa del neonato. Ecco perciò che sono i bambini a portare le cicogne e non viceversa!

La correlazione tra il numero di film in cui è apparso Nicolas Cage e il numero di persone morte annegate in piscina, tratto dal sito Spurious correlations
Esiste una sfilza di correlazioni molto alte tra variabili che intuitivamente non dovrebbero avere a che fare tra loro. Ne sono degli esempi il consumo di cioccolata pro-capite e il numero di premi Nobel per Stato, o il numero di persone che sono annegate cadendo in una piscina e i film in cui è apparso Nicolas Cage,[21] oppure ancora il tasso di divorzi nel Maine e il consumo pro-capite di margarina. Questo accade o per puro caso o perché tra le due variabili se ne nasconde una terza. Ad esempio, l’aspettativa di vita media degli abitanti di un Paese aumenta in funzione del numero di televisori pro-capite in quel Paese[22] non grazie ai poteri magici di guarigione da attribuire ai televisori, ma semplicemente perché il numero di televisori pro-capite e l’aspettativa di vita aumentano con la ricchezza complessiva del Paese. Così come qualsiasi correlazione tra le vendite di gelato e gli annegamenti è dovuta al fatto che i due fenomeni sono influenzati dalle condizioni meteo.
L’unica certezza è che lo stesso andamento di due variabili non significa che una sia causa dell’altra, cioè che la correlazione implichi un nesso casuale. Frase quest’ultima che dovremmo ripeterci come un mantra ogni mattina, dato che gli esseri umani hanno evidentemente una profonda necessità di spiegare gli avvenimenti con rapporti causa-effetto, sottovalutando la complessità del mondo in cui vivono. Tanto che è stato coniato un termine, apofenia, per indicare la tendenza a identificare nessi tra eventi non correlati tra loro.
Se gli esempi sino a qui mostrati erano piuttosto banali, vi assicuro che l’apofenia può nascondersi anche in casi più seri. Ad esempio, se vi dicessi che a molti bambini viene diagnosticato l’autismo poco dopo la somministrazione del vaccino combinato contro morbillo, parotite e rosolia, questo indicherebbe che i vaccini causano l’autismo? Un importante studio danese ha analizzato un campione di 650 mila bambini, gran parte dei quali avevano ricevuto il vaccino a 15 mesi d’età e un richiamo a 4 anni, mentre un campione più esiguo non ricevette alcuna dose. Molti bambini vaccinati ricevettero in effetti una diagnosi di autismo dopo la vaccinazione. Ma quando si guardarono i valori percentuali ci si accorse che la percentuale di diagnosi di autismo era la stessa in entrambi i gruppi. I due gruppi non differivano quindi dal punto di vista della presenza di diagnosi di autismo, in compenso la probabilità di contrarre le malattie sconfitte tramite quel prezioso vaccino era ovviamente più alta nel gruppo dei non vaccinati.[23]
Un altro esempio si trova nei decessi annuali: il fatto che la percentuale di mancini morti sia minore rispetto alla percentuale di mancini presenti nella popolazione totale proverebbe che i mancini vivono più a lungo? Forse dimostra soltanto che quando le persone che oggi muoiono erano piccole si obbligavano i bambini mancini a scrivere con la destra, così che i mancini anziani oggi sono rari. I papi muoiono a un’età media più avanzata rispetto alla media, ciò significa che diventare papa allunga la vita o che i papi vengono scelti quando hanno già un'età avanzata? Durante la Seconda guerra mondiale si notò che i bombardamenti alleati in Europa risultavano tanto più precisi quanto maggiore era il numero di caccia nemici decollati per intercettarli e quanto più intensa era la reazione della contraerea. In teoria sarebbe dovuto avvenire il contrario, se non fosse per il fatto che quando il cielo era nuvoloso i bombardieri avevano scarsa visibilità e per la stessa ragione la contraerea era minore. Un altro esempio è quello classico che lega il numero di vittime in un incendio a quello dei pompieri impiegati per spegnerlo: stranamente più pompieri si impiegavano, più vittime si registravano. Quindi si può pensare che impiegando meno pompieri si avrebbero meno vittime? Sarebbe splendido se fosse così, ma la cruda realtà è che entrambe le variabili dipendono da una terza: la dimensione dell’incendio.
Dato quindi che la correlazione non implica causalità, essa può solamente far sorgere in noi ipotesi che andranno però corroborate con studi progettati in maniera appropriata, così da poter giungere a conclusioni affidabili. Ed è proprio questo il lavoro che dovrebbe fare lo statistico, anche se spesso viene consultato solo quando si tratta di analizzare i dati raccolti, a frittata già fatta. Infatti, secondo una famosa affermazione del noto statistico Sir Ronald Fisher: «spesso consultare lo statistico dopo la conclusione di un esperimento equivale semplicemente a chiedergli di condurre un’autopsia. Al massimo potrà dire di che cosa è morto l’esperimento».
A saper riconoscere la regressione verso la media
Supponiamo che a un folto gruppo di bambini siano state sottoposte due versioni equivalenti di un test attitudinale. Se selezioniamo dieci bambini fra quelli che hanno avuto una performance migliore in una delle due versioni, molto probabilmente scopriremo che il loro rendimento nell'altra versione sarà stato piuttosto deludente. Viceversa, se selezionassimo dieci bambini tra quelli che hanno avuto una performance più deludente ad un test, alla seconda versione otterranno probabilmente un risultato migliore. Nella quotidianità si verificano molto spesso casi come questo che illustrano il fenomeno noto col nome di regressione verso la media.
La regressione è sempre risultata indigesta alla mente umana, non a caso fu riconosciuta e compresa per la prima volta duecento anni dopo la legge di gravitazione universale e il calcolo differenziale. Secondo lo statistico David Freedman, se in una causa civile o penale saltasse fuori l’argomento della regressione, la parte che fosse costretta a spiegarlo alla giuria perderebbe il processo. Questo perché la nostra mente è fortemente incline alle spiegazioni causali e non è in grado di gestire bene i meri dati statistici.
Fu Sir Francis Galton, brillante cugino di Charles Darwin, il primo a osservare questo fenomeno. Fu anche l’inventore dello studio delle impronte digitali, colui che verificò se la preghiera aumentasse la durata della vita dei predicatori rispetto a quella degli altri individui e quantificò l’ereditarietà di molti caratteri importanti. Galton elaborò persino un’ipotesi sul fascino delle donne viste dal finestrino del treno diretto da Londra a Glasgow, trovando che il fascino diminuiva in funzione della distanza da Londra. Un tipino interessante deve essere stato tale Galton, la cui massima era «Quando potete, contate». Ma bando alle ciance, egli nel 1886 pubblicò l’articolo Regression towards mediocrity in hereditary stature (Regressione verso la mediocrità nella statura ereditaria) in cui parlava dei suoi studi che avevano riguardato sia le dimensioni di varie generazioni di semi che la statura di bambini confrontata con quella dei loro genitori. Dei primi scrisse:
«Risultava da questi esperimenti che i semi figli non tendevano ad avere dimensioni simili a quelle dei genitori, ma più mediocri (oggi diremmo più vicine alla media, NdR), ovvero tendevano a essere più piccoli dei genitori se i genitori erano grandi, e più grandi dei genitori se questi erano molto piccoli [...] Gli esperimenti hanno dimostrato inoltre che la regressione filiale media verso la mediocrità era direttamente proporzionale alla deviazione parentale da essa.»
Questo perché ogni volta che la correlazione tra due punteggi è imperfetta (ovvero quando all’aumentare di una variabile l’altra non aumenta o diminuisce in modo esattamente proporzionale) si verifica il bizzarro fenomeno della regressione verso la media, che ha una spiegazione, ma non una causa. L’evento che attira la nostra attenzione al torneo di calcetto è il frequente peggioramento della prestazione dei giocatori che avevano avuto molto successo all’inizio del torneo. La migliore spiegazione del fenomeno è che quei giocatori abbiano avuto un’insolita fortuna all’inizio, ma la nostra mente preferisce una spiegazione interessante che giri intorno a una causa. D’altronde, stareste ad ascoltare un giornalista economico che vi spiegasse (correttamente, peraltro) che l’economia quest’anno è andata meglio perché l’anno scorso era andata male? Ma è esattamente così che funzionano le fluttuazioni casuali.
Se leggeste sui giornali un titolo tipo questo: I bambini depressi cui viene somministrata con regolarità una bevanda energetica migliorano sensibilmente in circa tre mesi sareste indotti a concludere che la bevanda energetica abbia il merito del miglioramento osservato. Ma è altrettanto vero che si potrebbe osservare un miglioramento anche nei bambini depressi che passino del tempo a testa in giù o con in braccio un gatto. Ciò non toglie che dare il merito a tali fattori sia una conclusione ingiustificata, in quanto la correlazione tra punteggi di depressione nelle varie occasioni è imperfetta, perciò vulnerabile all’effetto della regressione verso la media. Pertanto, per poter affermare che una cura sia efficace bisognerà confrontare un gruppo di pazienti ai quali tale cura sia stata somministrata con un altro gruppo, detto di controllo, al quale non viene somministrata. Mentre il gruppo di controllo dovrebbe migliorare esclusivamente per effetto della regressione verso la media, i miglioramenti del secondo gruppo dovrebbero essere maggiori di quelli determinati dalla regressione verso la media di quel sottogruppo.
Perché può letteralmente salvarvi la vita
Anche senza entrare nell’ambito della misteriosa Biostatistica, ci sono diversi esempi di statistici che con le loro intuizioni hanno salvato numerose vite. Uno dei più celebri fu John Snow, che non c’entra evidentemente nulla con l’omonimo personaggio di Game of Thrones. Questo medico inglese, durante un’epidemia di colera scoppiata nel quartiere londinese di Soho, segnò su una mappa tutti i contagiati e gli balzò subito all'occhio che il maggior numero di casi era in prossimità della fontanella di Broad Street. Il sospetto che quello fosse il focolaio dell’infezione trovò conferma nel fatto che questa era alimentata da un pozzo (invece che dall’acquedotto) scavato in prossimità di una fossa biologica. Ebbe così l’idea rivoluzionaria (per quei tempi) che il colera non fosse un disturbo del sangue, bensì dell’apparato digerente, che si trattasse di una malattia contagiosa e che si diffondesse attraverso la via orale-fecale, attraverso l'acqua contaminata. Non appena riuscì a convincere le autorità a chiudere il pozzo incriminato l’epidemia si placò. Questo evento passò alla storia come la prima dimostrazione dell’efficacia delle mappe per comprendere l’evoluzione di un’epidemia e gettò le basi dell'epidemiologia moderna.
Un altro esempio, seppur diverso, è quello dello Space Shuttle Challenger che esplose nel 1986 subito dopo il lancio provocando la morte di tutto il personale che era a bordo. Causa? Un errore statistico. Infatti il lancio era stato pianificato in un giorno con una temperatura incredibilmente bassa, in quanto i dati non mostravano alcun nesso fra la temperatura dell’aria e i danni alle guarnizioni dei razzi. Non si erano accorti di un dettaglio però: e cioè che i dati erano incompleti, in quanto non consideravano i lanci in cui non si erano verificati danni, che si erano svolti quasi tutti con temperature più alte.
E anche voi, che siate statistici o meno, potreste aiutare i ricercatori dell’Istituto Fondazione Italiana per la Ricerca sul Cancro di Oncologia Molecolare a salvare delle vite umane, semplicemente scaricando sul vostro smartphone l’app DreamLab. Questa si attiverà mentre il telefono è in carica e, usando la potenza di calcolo del vostro dispositivo, aiuterà a velocizzare i complicatissimi calcoli che sono sempre più necessari negli studi oncologici e non solo. Se un progetto richiede circa 100 mila ore di calcolo per essere portato avanti (circa un anno e mezzo), basterà che un migliaio di persone mettano in carica il telefono per 6 ore al giorno con DreamLab installato per far calare il tempo di calcolo a meno di un mese.[24] È proprio il caso di dirlo: l’unione fa la forza.
Ad essere buoni investigatori
Un'eclatante vicenda fu quella di Sally Clark, le cui due figlie di otto e undici settimane morirono in culla. Nonostante non fossero state trovate né prove né una possibile motivazione dell’omicidio, Clark nel 1998 fu accusata di duplice infanticidio dopo la testimonianza di un pediatra. Egli infatti fu chiamato a testimoniare in qualità di esperto e dichiarò che per la letteratura scientifica la morte in culla colpirebbe un bambino ogni 8.500, per cui la probabilità di tale evento è pari a 1/8.500. Alla domanda del giudice: Qual è la probabilità che due neonati muoiano per cause naturali? L’esperto rispose 1/8500 per 1/8500, cioè circa un caso su settantatré milioni. Verdetto della giuria: Sally Clark è colpevole!
Il problema è che non era corretto assumere che i due eventi fossero indipendenti (ovvero che l’avverarsi di uno non avesse interferito sul verificarsi dell’altro) e quindi non si potevano moltiplicare le rispettive probabilità, dato che fattori genetici e ambientali condivisi da membri della stessa famiglia aumentano le probabilità di morti in culla.
Inoltre, dalle statistiche ufficiali inglesi relative al 1997 si può osservare che la probabilità di due infanticidi compiuti dalla stessa persona era di circa uno su 2 miliardi. Era quindi molto meno probabile che Sally fosse colpevole piuttosto che innocente e proprio per questo Sally fu rilasciata ma non prima di aver scontato tre anni di carcere. Le tragedie della sua vita – la morte delle figlie prima e l’ingiusta condanna e carcerazione poi – possono aiutare a comprendere la causa della sua morte, un avvelenamento acuto da alcool, avvenuta a soli 42 anni.
Questo tipo di errore è noto col nome di fallacia dell’accusatore, dato che spesso ci si incappa nelle cause legali che si basano sui test del DNA. Ad esempio, quando uno specialista forense sostiene che se l’imputato è innocente c’è solo una probabilità su un miliardo che il suo DNA corrisponda a quello rinvenuto sulla scena del delitto. Ma poi interpreta questa affermazione in modo errato sostenendo che: «Dati gli indizi genetici, c’è solo una possibilità su un miliardo che l’imputato sia innocente». Questo è come sostenere che «se sei il papa sei cattolico» e saltare all'affermazione che «se sei cattolico sei il papa»”. Un errore logico più evidente, ma simile.
Un altro esempio di questa fallacia è emerso nella vicenda del campione di football americano O. J. Simpson, che fu assolto dall’accusa di aver ucciso l’ex moglie e il suo amante. Simpson aveva picchiato la moglie in almeno un’occasione ma il suo avvocato lo difese con i dati del Rapporto sulla Criminalità Ordinaria dell’FBI, secondo i quali su 4 milioni di donne picchiate dai compagni si sarebbero verificati solamente 1.432 omicidi. Perciò si attestava meno di un omicidio ogni 2.500 casi di maltrattamento. Quell'avvocato non doveva conoscere molto bene la statistica (o forse sì, e in tal caso ha approfittato dell’ignoranza del giudice), dato che – volendo risolvere il caso con la statistica – la probabilità da considerare era un’altra. Infatti, il ragionamento corretto da attuare in questo caso sarebbe stato: dato che una donna è stata assassinata e il suo compagno la picchiava, qual è la probabilità che sia stato lui ad ucciderla? Tale probabilità si calcola dividendo il totale delle donne uccise da chi le picchiava per il numero di donne picchiate e uccise. E tale probabilità è di circa il 90%. Una bella differenza.
A compiere scelte ragionate
I cervelli umani non elaborano molto bene le probabilità, come dimostra il fatto che tendiamo a giocare alla lotteria ma siamo spaventati quando saliamo su un aereo. Ci sono spiegazioni biologiche per questa tendenza, dato che sopravvalutare piccole probabilità che avrebbero esiti disastrosi ha aiutato i nostri antenati a sopravvivere. Ma nel mondo d’oggi, così dominato dall’incertezza, avere una mentalità statistica è sicuramente una caratteristica desiderabile che ci aiuta nella soluzione di problemi contro-intuitivi.
Un esempio lampante dell’innaturalità del pensiero probabilistico è il problema di Monty Hall, diventato particolarmente famoso dopo che nel film 21 Kevin Spacey lo propone alla sua classe. Si tratta di un gioco a premi in cui abbiamo di fronte tre porte chiuse e sappiamo che dietro a queste si nascondono due capre e una macchina, ma non sappiamo esattamente dove. Al giocatore viene chiesto di scegliere una delle porte, evento che avrà probabilità di successo (ammesso che siate interessati più a una nuova macchina che a una nuova capra) di un terzo. La porta che il giocatore ha scelto resterà chiusa e il conduttore del gioco – l’unico a conoscere la localizzazione del premio – aprirà una delle due rimanenti svelando una capra. A questo punto il conduttore offrirà al giocatore la possibilità di cambiare la sua scelta. Voi cosa fareste?
Saremmo intuitivamente portati a pensare che la probabilità di vincere la macchina sia sempre la stessa e perciò a non cambiare, ma non è così. Infatti, se rimanendo saldi alla nostra scelta iniziale la probabilità di ottenere una nuova macchina rimarrebbe di un terzo, il fatto di conoscere dove è posizionata una delle due capre fa sì che, cambiando, la probabilità di uscirne vittoriosi raddoppi. Ad essere onesti, dietro alla propensione a non cambiare c’è anche l’effetto psicologico per cui tendiamo a non cambiare la scelta già fatta per pigrizia, paura o per l'ancestrale convinzione che «chi lascia la via vecchia per la nuova, sa quel che lascia, e non sa quel che trova». Ma sarà veramente così?
Perché fidarsi è bene, ma non fidarsi è stupido
Immaginate di aver commesso un crimine con un complice. La polizia vi arresta e vi confina in due celle separate, ma – non essendo in possesso di prove a sufficienza per condannarvi – vi propone il seguente accordo. Se entrambi confesserete vi verrà data una pena di sei mesi; nel caso in cui entrambi neghiate la pena sarà per entrambi di solo tre mesi di reclusione, poiché le prove non sono altro che indizi; mentre se uno confessa e l’altro nega, allora la pena verrà ridotta ad un solo mese per chi ha ammesso la propria responsabilità e sarà estesa ad un anno per chi non l’ha fatto. Voi come vi comportereste?
La scelta razionale sarebbe quella di negare, dato che solo in questo modo scontereste il minor tempo complessivo in prigione. Però negando correte il rischio che l’altro invece confessi e, tradendovi, vi faccia rinchiudere per il tempo più lungo. Come potete essere certi del fatto che il vostro complice non vi tradirà, dato che non potete comunicare? Il prezzo in palio è decisamente alto e i dubbi vi attanagliano. La paura vi porterà così a confessare, sperando che l’altro neghi e vi permetta di ridurre la vostra pena ad un mese. Questi stessi ragionamenti potrebbe farli però anche il vostro complice, che arriverebbe così alla vostra stessa conclusione, ovvero che negare e permettervi di incastrarlo è un rischio troppo grosso da assumersi. E così vi ritroverete rinchiusi in prigione per il doppio del tempo rispetto alla pena che vi sarebbe stata inflitta se aveste intrapreso la scelta razionale di negare entrambi. Capite quindi come tutto questo sia viziato dalla mancanza di fiducia.
Questo classico esperimento di teoria dei giochi, noto col nome di Dilemma del Prigioniero, fu inventato dal matematico statunitense Albert Tucker e presentato per la prima volta all’Università di Stanford nel 1950. Ci viene richiesto di decidere tra negare la nostra responsabilità lasciando che la colpa ricada solo sull’altro o cooperare con il nostro complice per ridurre la pena che subiremo. Noi sappiamo che la nostra civiltà si basa sulla collaborazione, ciononostante, generalmente si tende in primis a pensare al nostro rendiconto personale. Ecco quindi che, se la fiducia viene meno, le persone tendono a prendere decisioni da cui ipotizzano di trarre un vantaggio personale, ma che si rivelano negative per tutti. Questo dilemma è tuttora estremamente attuale e può essere usato per comprendere molte situazioni del mondo reale che si basano sulla fiducia.
Ad esempio, se ci fossero solo due case automobilistiche al mondo, il prezzo a cui una mette in vendita le proprie macchine avrà una ripercussione diretta sul prezzo a cui l’altra le venderà. Se una scegliesse di venderle a un prezzo più alto rispetto alla concorrenza, finirebbe per vendere meno auto. Mentre se decidesse di venderle a un prezzo inferiore, si aggiudicherebbe anche i clienti del concorrente, perciò venderebbe più auto ma con un margine di profitto inferiore. Certamente, anche l’altra casa automobilistica ragionerà allo stesso modo, con il risultato finale che entrambe otterranno scarsi profitti. Proprio come l’interesse personale spinge i prigionieri del dilemma all’atto controproducente di confessare, qui potrebbe rendere difficile per i due concorrenti adottare un comportamento cooperativo.
Questo dilemma, evidenziando il motivo per cui due soggetti potrebbero non cooperare anche quando è nell’interesse di entrambi, aiuta a comprendere l’inarrestabile corsa agli armamenti che contrappose USA e URSS. In quest’ultimo caso, sebbene la strategia migliore fosse evidentemente quella di limitare l’arsenale per scongiurare il pericolo di una nuova grande guerra, fu proprio la mancanza di fiducia a spingere i due blocchi ad accumulare più armi possibili. A pensarci bene, è la medesima logica che sta alla base del possesso di armi: gli individui possono scegliere se avere una pistola o meno, la ricerca mostra come le società siano più sicure quando nessuno possiede armi, tuttavia alcune persone temono che qualcun altro abbia un’arma. In tal caso, ciò li metterebbe in una posizione di svantaggio, spingendoli a portare con sé una pistola. Vedete come in ognuno di questi casi qualcuno agisce nel proprio interesse perché crede che anche gli altri lo faranno.
In pratica, il dilemma del prigioniero dimostra che, quando gli individui perseguono solo il proprio interesse personale in un ambiente in cui il guadagno dipende anche dalle decisioni prese dagli altri, il risultato sarà peggiore rispetto a quello che avrebbero ottenuto nel caso in cui avessero cooperato. In un’epoca in cui le nostre vite sono caratterizzate come non mai dall’interdipendenza, è chiaro come questo dilemma possa insegnarci l’importanza di una collaborazione, sia nell’emissione di linee guida nazionali che nelle nostre azioni personali. Ad esempio, se indossare una mascherina riduce la quantità di goccioline nell’aria che si diffondono su una persona o che contaminano le superfici, il fatto di non indossarla mentre gli altri prendono questa precauzione avrà un impatto negativo sulla loro efficacia. Allo stesso modo, i paesi ricchi sfavorendo quelli poveri nell’accesso ai vaccini non stanno adottando la soluzione migliore, ma aggravano le disuguaglianze e contribuiscono all’emergere di nuove varianti del virus.
Come scrive il professore di Stanford Matthew Jackson: «Proprio come non puoi curare un’infestazione da termiti fumigando solo una stanza in una casa, non si può controllare la pandemia del Coronavirus indirizzando gli interventi a una regione o un paese specifico».[25]
Se a breve termine l’accumulo di vaccini può sembrare una vittoria per un Paese, si tratta di una perdita per altri. Se tutti i Paesi cooperano, il mondo può ottenere il risultato di sconfiggere la pandemia. Se non collaborano, il Covid si trascinerà e ci saranno inevitabilmente molti più decessi.
Siamo insomma di fronte all’eterno dilemma etico fra Callicle, che sosteneva la legge del più forte, e Socrate, secondo il quale la giustizia richiede cooperazione e una visione che comprenda sia i forti che i deboli. Nel nostro contesto pandemico, Callicle si chiederebbe: perché i politici dei paesi ricchi non dovrebbero acquistare i vaccini e dare prima l’immunità di gregge ai propri elettori? Mentre per Socrate il mondo starebbe meglio se li condividessimo, in quanto la mia sopravvivenza è interconnessa alla tua salute. E la scienza è dalla parte di Socrate.
A non lasciarsi abbindolare da titoli pulp
La scarsa educazione al metodo statistico gioca un ruolo anche nel fenomeno dell’analfabetismo funzionale - ovvero di chi sa leggere e scrivere, ma ha difficoltà a comprendere testi semplici (literacy) ed è privo di molte delle competenze di calcolo (numeracy) utili alla vita quotidiana. E c’è chi approfitta di questo nostro tallone d’Achille. Per esempio Ryanair, che nel 2017 annunciò che il 92% dei suoi passeggeri si era dichiarato soddisfatto di aver volato con loro. Il problema è che il sondaggio prevedeva solamente le seguenti possibili risposte: eccellente, ottimo, buono, soddisfacente e passabile.[26]
O di come molti mass-media riportarono l’inchiesta di qualche anno fa (documentata nel libro Wehler, C. A. (1991). A survey of childhood hunger in the United States. Community Childhood Hunger Identification Project) che rivelava che 11,5 milioni di bambini statunitensi rischiavano di morire di fame.[27] In seguito si scoprì che erano stati giudicati a rischio se i loro genitori avevano risposto affermativamente almeno a una domanda di un gruppo di otto tra cui: «Ha mai avuto problemi a nutrire i suoi figli perché stava finendo i soldi?».
In un articolo apparso su Internazionale il giornalista inglese David Randall elencò alcune affermazioni clamorose, come quella secondo cui «sono più gli afroamericani in prigione di quelli che frequentano un college». Considerando che i detenuti possono avere tra i 16 e i 96 anni, mentre l’età degli studenti universitari generalmente va dai 18 ai 23 anni, si vede che in realtà tra gli afroamericani di quest'ultima fascia d’età gli studenti universitari sono quasi il triplo dei detenuti.[28] Un altro esempio analogo riguarda una denuncia che nel 1997 venne formulata contro un laboratorio sostenendo che il 29% degli ex dipendenti era morto di cancro. Inquietante? Non proprio, dato che il cancro è la causa di morte del 35% delle persone tra 44 e 65 anni.
Dobbiamo tenere presente che i titoli sensazionali dei giornali cercano di stuzzicare la nostra curiosità. Con interpretazioni allarmistiche dei dati tentano di fare più colpo sul lettore. Il pezzo, pubblicato sul Corriere della Sera del 25 agosto 2003, intitolato: Gli automobilisti corretti? Solo l’8% ne è un esempio. Dal titolo siamo portati a concludere che quasi tutti gli automobilisti siano scorretti, quando in realtà i dati su cui si basava l’articolo e che categorizzavano gli automobilisti in base alla correttezza della guida, sono i seguenti: guidatori corretti (8%); guidatori non completamente corretti (86%); guidatori scorretti (6%). Quindi un titolo altrettanto parziale e veritiero rispetto a quello scelto avrebbe potuto essere: Gli automobilisti scorretti? Solo il 6%. E avrebbe trasmesso l’informazione opposta. Questo perché un dato decontestualizzato è veritiero quanto un fotogramma ritoccato.
Il problema non riguarda peraltro solo i mass-media: uno studio ha rilevato che nel 40% dei 462 comunicati stampa delle università britanniche pubblicati nel 2011 si trovano consigli esagerati, nel 33% nessi causali esagerati e nel 36% sono state rilevate conclusioni esagerate relative agli esseri umani partendo da studi sugli animali.[29] Più o meno strumentalmente, quindi, ricercatori e uffici stampa, giornalisti e commentatori forzano talvolta la lettura e l’interpretazione dei dati statistici, perpetuando quella che il prof. Milo Schield chiama prevaricazione statistica, e che consiste «nell’alterare la verità attraverso un’ambiguità, un equivoco o un’omissione».[30]
Non fraintendetemi, esiste un giornalismo scientifico di qualità, ma ne esiste anche uno scadente. Per distinguerli dopo aver letto un articolo, provate a chiedervi come potreste riassumerlo ad un amico. Avete capito cosa hanno fatto i ricercatori e perché? Cosa veniva misurato? Lo studio era stato effettuato su umani o su cavie? Il risultato era inatteso per la comunità scientifica? Un bravo giornalista deve specificarlo.
Un sensazionale esempio di prevaricazione statistica si presentò quando l’Agenzia internazionale per la ricerca sul cancro dell'OMS (IARC) annunciò che la carne lavorata rientrava nel gruppo I delle sostanze cancerogene, la stessa delle sigarette e dell’amianto. Ed ecco che una mattina ci siamo svegliati con l’articolo de Il Fatto Quotidiano intitolato: “Alimenti cancerogeni, Oms: 'Wurstel, prosciutto e carni lavorate possono causare il cancro. Dannosi come il fumo’”. L’IARC ha tentato poi di spiegare che tale classificazione è dovuta alla certezza di un maggiore rischio di cancro, e che l’assunzione quotidiana di 50 grammi di carne lavorata è associata ad un aumento del 18% del rischio di tumore del colon-retto. Ciò significa che se ci si aspettano 6 casi di tumore del colon-retto su 100 persone che non mangiano quotidianamente carne lavorata, ci aspettiamo un caso in più tra altre 100 simili ma con una passione sfrenata per i wurstel. Avete capito la portata dello scoop ora?
A sapere che la significatività statistica non sempre è significativa
Uno studio[31] ha dimostrato che gli incidenti automobilistici aumenterebbero significativamente nei periodi di luna piena e ovviamente questo risultato ha attratto l’attenzione dei media, in quanto ha fatto subito pensare a vicende di lupi mannari e vampiri. Ma tale aumento era solo dell’1%, troppo piccolo quindi per indurci a lasciare la macchina a casa quando la luna splende piena in cielo.
All’inizio del secolo scorso, col termine “significativo” si intendeva che qualcosa significava o mostrava un concetto. Per lo statistico Ronald Aylmer Fisher un risultato significativo si aveva quando i dati indicavano una certa differenza dall’ipotesi che voleva confutare. Al giorno d’oggi il termine “significativo” tende ad essere confuso col termine “importante” e ciò crea ambiguità. Ad esempio, se un articolo giornalistico descrive un nuovo risultato scientifico come un “nuovo risultato significativo” o un “progresso significativo nella nostra conoscenza”, si tratterà di un enunciato statistico oppure di un giudizio di valore? Spesso il significato si confonde, dato che un risultato statisticamente significativo non è sinonimo di un risultato rilevante.
Effetti minuscoli e irrilevanti possono risultare statisticamente significativi se si ha a disposizione un campione molto grande, ecco perché è buona prassi ambire a dimostrare differenze importanti. D’altra parte, un risultato può essere importante anche se non è statisticamente significativo, come quando nuovi dati suggeriscono un pattern che, se verificato, potrebbe essere importante per capire un fenomeno sconosciuto e indurre quindi ad approfondire uno studio. Come è successo, ad esempio, quando uno studio su larga scala sull’efficacia della terapia ormonale sostitutiva (TOS) non ha mostrato evidenze statisticamente significative del beneficio della TOS sulle donne in post-menopausa.
Questa terapia era stata ampiamente usata, anche con un notevole investimento di denaro e con alcuni effetti collaterali deleteri; perciò scoprire che era di scarso beneficio ha permesso di risparmiare una grande quantità di risorse e di prevenire questi effetti collaterali. Questo risultato non era statisticamente significativo, ma fu decisamente importante.
In altri casi invece l’associazione può essere statisticamente significativa... senza che questo significhi davvero qualcosa. Simonsohn e i suoi colleghi[32] chiesero ad alcuni studenti dell’Università della Pennsylvania di ascoltare “When I’m sixty-Four” dei Beatles, oppure “Kalimba” o “Hot Potato” dei Wiggles per poi chiedere loro l’età. Ripetendo le analisi dei dati in ogni modo possibile e continuando ad aggiungere soggetti allo studio, alla fine Simonsohn riuscì ad ottenere un’associazione significativa, dimostrando così che ascoltare la canzone dei Beatles renderebbe più giovani. Lo scopo dei ricercatori in questo caso era proprio quello di dimostrare che – citando lo scrittore Gregg Easterbrook – «Se torturi i numeri abbastanza a lungo, confesseranno qualsiasi cosa»
A capire l’importanza della variabilità
La poesia che Trilussa dedicò qualche secolo fa alla statistica è molto conosciuta:
Sai ched’è la statistica? È na’ cosa
che serve pe fà un conto in generale
de la gente che nasce, che sta male,
che more, che va in carcere e che spósa.
Ma pè me la statistica curiosa
è dove c’entra la percentuale,
pè via che, lì, la media è sempre eguale
puro co’ la persona bisognosa.
Me spiego: da li conti che se fanno
seconno le statistiche d’adesso
risurta che te tocca un pollo all’anno:
e, se nun entra nelle spese tue,
t’entra ne la statistica lo stesso
perch’è c’è un antro che ne magna due.
Er compagno scompagno:
Io che conosco bene l’idee tue
so’ certo che quer pollo che te magni,
se vengo giù, sarà diviso in due:
mezzo a te, mezzo a me... Semo compagni.
No, no - rispose er Gatto senza core -
io non divido gnente co’ nessuno:
fo er socialista quanno sto a diggiuno,
ma quanno magno so’ conservatore.
Questo sonetto divertente ed elegante è ben poco generoso con la statistica e con una delle sue misurazioni più spesso utilizzate: la media. Sulla povera media aritmetica circolano vecchie battute secondo le quali quasi tutti hanno un numero di gambe maggiore della media (probabilmente vicina a 1.99999) e che in media ogni persona ha un testicolo.
Questo perché la media è solo un numero e nel caso di un campione poco omogeneo può somigliare poco all’esperienza dei più, rischiando di risultare fuorviante data la sua tendenza a lasciarsi influenzare dai valori estremi. Ad esempio, se nel campione che intervisto per un’indagine sul reddito dichiarato fosse incluso insieme a voi Bill Gates, la media non si avvicinerà più al vostro reddito. Questo perché la media è solo un indice di posizione, ovvero una delle diverse misure di tendenza centrale esistenti, e da sola non può bastare a rappresentare i dati, ma è necessario accompagnarla almeno con un indice di dispersione, come la variabilità che ci dica quanto tale numero è rappresentativo.
Infatti, se la media della poesia di Trilussa è sempre di un pollo a testa, sia che anch’io lo mangi o che lui li mangi entrambi, con un semplice calcolo della varianza si scopre l’inganno. Infatti, la varianza che nel primo caso sarebbe nulla (indicando che ad entrambi è toccata la stessa quantità), nel secondo caso risulta maggiore di 0. Gli statistici conoscono bene l’importanza della variabilità, dato che la statistica senza questa non serve a nulla. Se ci pensate, sapere il numero di scarpe medio dell’uomo adulto non aiuterà i produttori a decidere la quantità di scarpe di ogni misura da fornire ai consumatori, in quanto la stessa misura non andrà mai bene per tutti, come ci ricordiamo ogni volta che su un aereo ci ritroviamo stipati nel nostro sedile.
A restare affascinati dalla simmetria dell'universo
Nel 1809 Carl Friedrich Gauss (lo scienziato che si poteva ammirare sulle banconote da 10 marchi tedeschi prima dell'avvento dell'euro) stava studiando gli errori di misura in astronomia e nei rilevamenti topografici, quando si accorse che incappava spesso in una strana curva a campana. Questa rappresenta la distribuzione delle frequenze più elevate per i valori centrali, mentre in corrispondenza di quelli più estremi tende progressivamente a diminuire. E tale curva può descrivere moltissimi fenomeni. Si tratta di una regolarità della natura veramente straordinaria e perciò fu battezzata col nome di “distribuzione Normale”, in quanto rappresentava la “norma” per qualsiasi distribuzione presente in natura. Oggi sappiamo come moltissime caratteristiche si distribuiscono secondo una curva a campana e possono essere quindi approssimate con la distribuzione Normale (detta anche “curva Gaussiana”). Ne sono degli esempi la temperatura corporea delle persone adulte, la dimensione dell’encefalo degli studenti universitari e il numero di setole sull’addome dei moscerini della frutta. Anche Francis Galton rimase affascinato dal fatto che tale distribuzione, all’epoca detta Legge della frequenza degli errori, emergesse sistematicamente da situazioni di caos apparente. Ne scrisse:
«Non conosco niente che possa colpire l’immaginazione quanto la forma meravigliosa di ordine cosmico espressa dalla “Legge della frequenza degli errori”. Se i greci avessero conosciuto questa legge, l’avrebbero personificata e divinizzata. Essa regna in serenità e totale modestia, tra la confusione più selvaggia. Maggiore è la folla e l’apparente anarchia, più perfetto è il suo dominio. È la suprema legge dell’Irragionevolezza. Ogni volta che si richiama all’ordine un grande campione di elementi caotici e li si inquadra secondo le loro dimensioni, si scopre che una forma insospettata e meravigliosa di regolarità era presente da sempre.»
A non fidarsi di un solo studio
Archie Cochrane era un medico, epidemiologo e attivista che nel 1941, mentre era prigioniero di guerra nelle mani dei tedeschi, decise di improvvisare uno studio clinico. Dato che molti dei prigionieri (lui incluso) erano malati e Cochrane sospettava che la causa fosse una carenza dell’alimentazione, mise a confronto l’effetto di diete diverse. Riuscì così ad appurare cosa mancava alla dieta dei prigionieri e a portare prove incontrovertibili al comandante capo. Così facendo i prigionieri ricevettero integratori vitaminici che salvarono la vita a molti di loro[33].
Nel 1979 Cochrane scrisse: «una grave carenza nella nostra professione è il fatto di non avere predisposto la realizzazione di un elenco critico, suddiviso per specialità e aggiornato periodicamente, di tutti gli studi clinici controllati e randomizzati.» Effettivamente, data la folta schiera di bias che – come abbiamo visto – possono compromettere gli studi, capite come questi – se presi singolarmente – siano troppo vulnerabili per essere ritenuti attendibili. Infatti, molto raramente un singolo studio clinico ben condotto e ben scritto fornisce prove solide sugli effetti di un trattamento, anche soltanto per un problema di generalizzabilità dei risultati. Inoltre, se si confrontano ad esempio due trattamenti, eventuali differenze potrebbero essere dovute al caso, ma un campione non sufficientemente grande potrebbe non evidenziarlo.
Dopo la morte di Cochrane, Iain Chalmers portò avanti la sua battaglia, riuscendo a dare luce a un gruppo di ricercatori provenienti da tutto il mondo impegnati a revisionare, valutare, riassumere e pubblicare i migliori dati disponibili su un’ampia gamma di studi clinici: la Cochrane Collaboration. Sul sito della Cochrane oggi si possono trovare descrizioni sintetiche e chiare dello stato dell’arte in varie aree cliniche. Un gruppo che si prefigge il medesimo obiettivo per quanto riguarda le scienze sociali è la Campbell Collaboration. Ecco che così, verso la fine del 20° secolo abbiamo iniziato ad accettare l’idea che l’analisi di analisi provenienti da studi simili (ovvero la meta-analisi) e la valutazione critica e la sintesi di tutti gli studi rilevanti su un argomento specifico (ovvero le revisioni sistematiche) fossero strumenti importanti per evitare di trarre conclusioni errate. Un singolo studio sulle statine può dirci che il farmaco ha funzionato per un certo gruppo in un certo luogo, ma occorrono vari studi per corroborare il risultato riscontrato. Perciò si svolgono rassegne sistematiche e meta-analisi che includono tutti gli studi simili svolti sul tema, così che sia possibile – combinando i loro dati o i loro risultati – prendere una decisione razionale in merito.
La prima meta-analisi fu pubblicata da Karl Pearson nel 1904 e da allora il numero di revisioni sistematiche e meta-analisi pubblicate è aumentato rapidamente. Ad esempio, dagli anni ’50 agli anni ’90 più di centomila neonati sono morti in culla (SIDS). Il pediatra Benjamin Spock in quel periodo vendette 50 milioni di copie del suo libro intitolato Baby and Child Care, nel quale scriveva: «Penso che sia preferibile abituare un bambino a dormire a pancia in giù fin dall’inizio, se vuole» e con lui altri colleghi formularono raccomandazioni simili. Ma all’inizio degli anni Novanta alcuni ricercatori si resero conto che il rischio di SIDS si dimezzava se i bambini venivano addormentati sulla schiena, invece che a faccia in giù, e le successive campagne educative riuscirono a portare a un drastico calo del numero di decessi per morte in culla. Tuttavia, erano disponibili già dal 1970 ricerche che mostravano come dormire a pancia in giù fosse pericoloso per i neonati. Perciò una sintesi anticipata dei dati avrebbe potuto salvare molte vite.
Consultando i riassunti che Cochrane mette a disposizione mi è sorto un dubbio. Così ho provato a googlare “lo yoga cura l’incontinenza?” e tutti i primi risultati annunciavano che secondo la scienza c’erano prove sufficienti in questo senso, cantando le lodi dello yoga. Per capire davvero le cose sono dovuta tornare sul sito della Cochrane, dove si concludeva invece che: «Abbiamo identificato pochi studi sullo yoga per l’incontinenza e gli studi esistenti erano piccoli e ad alto rischio di bias. [...] A causa della mancanza di prove per rispondere alla domanda, non siamo sicuri che lo yoga sia utile per le donne con incontinenza urinaria. Sono necessari ulteriori studi ben condotti con campioni di dimensioni maggiori.» In questo caso la disinformazione non avrebbe fatto grandi danni, al massimo avremmo fatto un po’ di yoga, ma se la disinformazione toccasse aspetti vitali? In questo caso il risultato potrebbe rivelarsi fatale.
Le meta-analisi ci permettono quindi di generalizzare i risultati, consentendoci di determinare l’importanza e la coerenza degli effetti su una varietà di sistemi. Talvolta revisioni sistematiche e meta-analisi mostrano che non esistono ancora prove affidabili, altre volte confermano come l’evidenza attendibile proviene da un solo studio, ma anche questi sono risultati importanti da evidenziare. Oggi la maggiore disponibilità di questi "riassunti di dati" sta migliorando la qualità delle informazioni, ma comunque neanche questi devono essere accettati acriticamente, in quanto a loro volta sono frutto di scelte umane e quindi vulnerabili ai bias. Infatti, diverse revisioni che affrontano lo stesso quesito a volte arrivano a conclusioni diverse, dato che i loro autori possono selezionare, analizzare e presentare prove in modi che supportano i loro pregiudizi e interessi. Ad esempio, nel libro Come vivere più a lungo e sentirsi meglio, Linus Pauling (l’unica persona al mondo che ha ricevuto due premi Nobel non in condivisione) ha citato ben trenta studi a sostegno della sua idea che grandi dosi giornaliere di vitamina C riducono il rischio di contrarre il comune raffreddore, ma non ne ha nominato nemmeno uno contrario all’idea, anche se ne erano disponibili un gran numero.
Lo statistico britannico David John Hand ha scritto: «Come i telescopi, i microscopi, i raggi X e i radar, la Statistica moderna consente di vedere cose invisibili a occhio nudo». Ciò è vero, com’è vero che se uno davanti a un telescopio chiude gli occhi non vedrà mai nulla.
A vedere l’errore come un indicatore di precisione
Dal momento che in statistica si cerca di rispondere a quesiti sulla popolazione generale a partire da un campione necessariamente ristretto, la stima che ne deriverà dovrebbe essere abbastanza umile da accompagnarsi a una stima dell’eventuale errore commesso nel processo di inferenza. Ecco perché uno statistico non si fiderebbe mai di una stima “puntuale”, ovvero così ingenua da viaggiare sola, senza un “intervallo di confidenza”, ovvero senza un intervallo di valori che, con un dato grado di fiducia, conterrà il vero parametro stimato. Un po’ come quando, prima di partire per una gita fuori porta, non guardiamo alla temperatura attesa a mezzogiorno per organizzare la valigia, ma ci informeremo piuttosto sulla temperatura minima e massima, perché le riteniamo stime più importanti.
Ovviamente l’intervallo di confidenza sarà più ampio al diminuire del grado di sicurezza impostato (più voglio essere certo che questo comprenda il valore reale, più ampio sarà l’insieme delle possibili stime), al crescere della variabilità del fenomeno studiato (se un fenomeno è ben definibile sarà più facilmente individuabile) e al diminuire della grandezza del campione (più grande è la proporzione di popolazione intervistata, più informazioni avrò sul valore reale). Il calcolo dell’intervallo di confidenza si basa sull’errore standard, che altro non è che un indice di variabilità che sarà tanto più piccolo quanto più attendibile sarà la stima a lui associata. Questo ragionamento fa parte dei fondamentali della cosiddetta statistica inferenziale, ma a quanto pare non è noto a tutti coloro che ci forniscono i dati.
Ad esempio, nel 2018 il sito BBC News annunciò che sul finire dell'anno precedente i disoccupati in Gran Bretagna erano diminuiti di 3000 unità e che in quel momento erano stimati pari a 1.44 milioni. Dimenticando di menzionare il fatto che questa stima, basata su un sondaggio svolto su 100 mila persone, aveva un margine d'errore di 77 mila unità, il che significa che il dato reale della disoccupazione poteva vedere, rispetto all’anno precedente, un aumento di 80 mila o una diminuzione di 3 disoccupati.
A dare il giusto peso ai dati
Attualmente i dati sono fra i beni che valgono di più sul mercato, poiché permettono alle aziende di conoscere le nostre abitudini, i nostri gusti e di tracciare il nostro profilo così da consigliare a potenziali futuri clienti i prodotti che si addicono di più ai loro gusti. I nostri dati nelle mani di Amazon, Apple, Facebook, Google e Microsoft rappresentano una vera e propria miniera d’oro. Ad esempio, Netflix e Amazon Prime hanno i dati su cosa guardiamo, quando lo guardiamo e possono sapere addirittura se abbiamo interrotto la visione; tali dati possono essere analizzati, incrociati e talvolta condivisi con altre aziende che li rivenderanno. Ogni volta che facciamo una ricerca su Google, o effettuiamo un pagamento online, twittiamo o regoliamo la temperatura di casa col termostato smart produciamo dati che solitamente servono a fornirci un servizio più personalizzato e quindi fatto ad hoc per noi. Le carte fedeltà che avete nel portafoglio ne sono un altro esempio. Invece di essere semplicemente un modo per usufruire di sconti al raggiungimento di una determinata spesa, per gli esperti di marketing rappresentano la chiave per capire i vostri gusti e tentare di fidelizzarvi. Senza la promessa dei punti, i clienti non avrebbero nessun motivo per usare una carta e rendersi riconoscibili ogni volta che fanno la spesa.
Il giornalista americano Charles Duhigg[34] ha raccontato in un articolo sul New York Times la storia emblematica di un uomo infuriato che andò a lamentarsi col responsabile di “Target”, uno dei più popolari grandi magazzini statunitensi, del fatto che sua figlia adolescente avesse ricevuto dei coupon per l’acquisto di vestiti per neonati e premaman. Il responsabile si scusò e, quando a qualche giorno dall’evento volle richiamare l’uomo, si sentì porgere delle scuse, in quanto il cliente aveva scoperto che sarebbe presto diventato nonno. Ecco il potere degli algoritmi! Infatti, da un acquisto insolito della ragazza, come ad esempio degli integratori di acido folico specifici per donne incinte, per l’algoritmo di Target – che aveva accesso a questa informazione – sarebbe stato molto semplice prevedere un inizio di gravidanza. Ma siccome da grandi poteri derivano grandi responsabilità, talvolta chi possiede i nostri dati ci invia – oltre ai coupon con sconti personalizzati – anche coupon casuali, proprio per non far trapelare che l’azienda ci conosca meglio di quanto crediamo[35]. Insomma, è proprio vero che nessuno fa niente per niente. Basta esserne consapevoli.
A non lasciarsi travolgere dalle coincidenze
Siamo tutti portati a pensare che le coincidenze che sperimentiamo nella vita possano essere segni del destino. Le coincidenze ci affascinano e ci piace dare significati a eventi tanto improbabili da sembrarci assurdi. Senza sapere che la maggior parte delle coincidenze della nostra vita – come ad esempio incappare nel nostro vicino di casa mentre ci troviamo dall’altra parte del mondo, conoscere una persona con la quale condividiamo lo stesso compleanno oppure sognare un evento prima che questo si verifichi – possono essere spiegate con semplici considerazioni matematiche. Se ci sembrano così sorprendenti è perché non conosciamo le leggi di probabilità.
Un esempio noto risale ai primi anni Settanta, quando l’attore Anthony Hopkins venne ingaggiato per interpretare una parte nel film La ragazza di via Petrovka. Dopo aver cercato, senza successo, in diverse librerie il romanzo da cui il film è tratto, decise di rincasare, quando notò su una panchina della metropolitana una copia del libro che stava cercando. E, come se ciò non bastasse, scoprì poi che si trattava proprio della copia che l’autore del romanzo aveva perduto tempo addietro. Qual è la probabilità che un evento del genere accada? Uno su un milione? Uno su un miliardo? Mazur[36] l’ha calcolata e la probabilità che a qualcuno accada qualcosa di simile è prossima a quella di ottenere una scala reale a poker. Quindi difficile sì, ma non impossibile. Questo perché le coincidenze sono inevitabili, dato che anche ciò che è straordinariamente improbabile qualche volta dovrà pur accadere.
Un altro esempio di coincidenza apparentemente incredibile è quella avvenuta nella famiglia inglese Allali, in cui tutti e tre i figli sono nati lo stesso giorno in anni diversi. Il Daily Mail ha riportato la notizia affermando che si tratterebbe di un evento che capita una sola volta su 48 milioni, numero ottenuto moltiplicando tre eventi con probabilità di uno su 36.536. Ma – assumendo che la famiglia Allali non stesse cercando di seguire un piano familiare incredibilmente meticoloso, che non esistano anni bisestili (per praticità) e che un bambino abbia la stessa probabilità di nascere in ogni giorno dell’anno – dato che il primo figlio avrebbe potuto nascere in qualsiasi giorno, non dovrebbe comparire nella formula. Perciò, moltiplicando le probabilità di due eventi ciascuno pari ad uno su 365[37], risulta una probabilità di uno su 133 mila. Ciò fa di questo evento un caso raro, ma siccome in UK esistono circa 1 milione di famiglie con tre figli, ci dovremmo aspettare circa 7 casi di questo tipo all’anno. Capite quindi perché ciò che ci sembra impossibile, in realtà non lo è?
Il paradosso del compleanno è un classico esempio di questo tipo. Tale paradosso dimostra come bastino solamente 23 persone per rendere più probabile che improbabile il fatto che due fra queste spengano le candeline lo stesso giorno. In realtà, per quanto sembri incredibile, con sole 57 persone ne saremmo praticamente certi. Assurdo, vero? Eppure, se ci riflettiamo, 66 milioni di anni fa una cometa si schiantò vicino alla penisola dello Yucatan e quell’esplosione fu probabilmente responsabile dell’estinzione dei dinosauri e quindi, a catena, dell’evoluzione delle specie rimanenti e dell’avvento degli esseri umani. E se l’orbita di quella cometa si fosse trovata appena un chilometro più in là? Un chilometro non è nulla in scala astronomica, eppure sarebbe stato sufficiente a non far estinguere i dinosauri. Ecco perciò che gli umani sono figli di una coincidenza e l’importante è saperlo per continuare ad esserne affascinati, ma non sopraffatti.
Detto ciò, nemmeno gli statistici sono immuni dagli errori. Lo hanno dimostrato lo psicologo premio Nobel Daniel Kahneman e il suo collega Amos Tversky[38] ponendo ad alcuni ricercatori in psicologia domande statistiche non formulate in modo formale, tipo questa: supponete di vivere in una città in cui vi siano due ospedali, uno grande e uno piccolo. In un dato giorno, il 60% di bambini nati in uno dei due ospedali è maschio. Di quale dei due ospedali è più probabile che si tratti? Dato che i campioni più sono grandi, più tendono a fornire stime che si discostano poco dalla media reale, e dato che in media nascono 101 maschi ogni 100 femmine, la risposta corretta è l'ospedale più piccolo. Ma la maggior parte dei ricercatori non ci pensò e sbagliò.
Ma l’esempio madre di scivolone statistico ci è fornito da Sir Ronald Fisher, la figura più importante nella storia della statistica. Considerato uno dei grandi geni del secolo scorso, a lui dobbiamo anche la genetica teorica delle popolazioni, ma nessuno è perfetto, si sa. Infatti Fisher era anche un accanito fumatore e mentre era consulente scientifico del Tobacco Manufacturers’ Standing Committee si disse convinto che «La teoria che il cancro al polmone è causato dal fumo verrà alla fine considerata un grandissimo, catastrofico errore[39]». Lo studioso aveva avanzato infatti l’ipotesi secondo la quale sarebbe esistita una particolare predisposizione genetica che incide sia sulla comparsa delle malattie legate al fumo che sull’abitudine a fumare. La statistica, che rimane il miglior antidoto contro il pregiudizio, lo ha nel frattempo smentito. Perché apprendendo la statistica si prova la stessa sensazione che sperimentano i miopi indossando gli occhiali: tutto diventa improvvisamente più nitido.
«Dr Manhattan: – Eppure durante ogni accoppiamento umano migliaia di milioni di spermatozoi lottano per lo stesso uovo. Moltiplica queste probabilità contrarie per generazioni. Contro le probabilità che i tuoi antenati siano vivi, che si incontrino, che generino precisamente quel figlio, esattamente quella figlia... Fino a quando tua madre ama un uomo che ha tutte le ragioni per odiare e da quell’unione fra milioni di bambini potenziali in competizione sei stata tu, e solo tu, a emergere. Distillare una forma così specifica da un simile caos di improbabilità è come trasformare l’aria in oro... È l’improbabilità suprema.
Laurie: – Potresti dire lo stesso di chiunque altro al mondo!
Dr Manhattan: – Sì, chiunque altro. Ma il mondo è così affollato di persone, così affollato di persone, così affollato di questi miracoli, che diventano comuni e ce ne dimentichiamo!»
Watchmen, Alan Moore
Se anche l'AIFA sbaglia
Nessuno è perfetto, dicevamo, nemmeno l'Agenzia Italiana del Farmaco. Che nel Rapporto Annuale sulla Sicurezza dei Vaccini COVID-19 ha clamorosamente sbagliato l’analisi del confronto fra decessi osservati e attesi nei 14 giorni successivi alla somministrazione del vaccino anti Covid (pagine 24-26)[40]. Nonostante la statistica fosse sbagliata, la conclusione presentata era giusta e mostrava che non esiste un'associazione tra la somministrazione del vaccino e il numero di decessi nelle settimane successive. In ogni caso, si è trattato di un errore grave.
Vediamo quel che è successo. Sono stati confrontati i decessi previsti (attesi) per fasce d'età in un periodo di due settimane con quelli osservati nei quattordici giorni successivi alla somministrazione del vaccino. «L’analisi osservati-attesi (analisi O/A) ha lo scopo di confrontare il numero di eventi che si sono effettivamente verificati in una popolazione esposta a un ipotetico fattore di rischio (casi 'osservati’), con il numero di eventi che si sarebbero verificati in condizioni naturali in assenza del fattore di rischio (casi 'attesi’)», scrivono. L’ipotetico fattore di rischio è il vaccino, la popolazione esposta sono tutti i vaccinati.

Tabella 1 - Soggetti totali vaccinati in Italia al 26 dicembre 2021 con 1a dose
TMS=Tasso di mortalità standardizzato; IC95% Intervallo di confidenza al 95%.
TMS=Tasso di mortalità standardizzato; IC95% Intervallo di confidenza al 95%.
L’AIFA stima i casi attesi, ovvero il numero di decessi che ci saremmo aspettati in quella stessa popolazione di soggetti in assenza di vaccinazioni, usando la probabilità di decesso osservata nel 2019 in un periodo di 14 giorni causata dalla normale mortalità (per vecchiaia, per incidenti, per malattie…). Ovviamente, dato che la mortalità è più bassa per i giovani e più alta per gli anziani, l’analisi è stata condotta per fasce di età. Queste poi sono state confrontate con quelle osservate nella realtà, ovvero dopo l’esposizione al vaccino. I casi osservati dovrebbero essere quindi tutti i decessi avvenuti entro 14 giorni dalla somministrazione del vaccino, ma invece di prendere tutte le morti avvenute dopo il vaccino per ogni causa, l’AIFA decide che «i casi osservati coincidono con tutte le segnalazioni ricevute nei 14 giorni successivi alla somministrazione dei vaccini anti-COVID-19». Ma fra tali segnalazioni non ci sono le morti da incidenti e tante altre cause fatali che invece vengono correttamente considerate nel calcolo delle morti attese. Questo equivale a confrontare un cesto di frutta con un altro, del quale però si considerano solo le banane. Così facendo, le morti osservate sono irrisorie rispetto alle morti attese. Ma anziché stupirsi del fatto che i due numeri, morti attese e morti osservate, che dovrebbero essere simili tra loro, siano in realtà così distanti, l’AIFA conclude che «i decessi osservati sono sempre nettamente inferiori ai decessi attesi e non c’è quindi, nella popolazione di soggetti vaccinati, alcun aumento del numero di eventi rispetto a quello che ci saremmo aspettati in una popolazione simile ma non vaccinata.» Così facendo avrebbero potuto paradossalmente dichiarare che il vaccino protegge anche da morte per incidente stradale!
L’insegnamento della statistica in Italia
Intervista a dott.ssa Rina Camporese, dott.ssa Patrizia Collesi, dott.ssa Susi Osti dell’ISTAT
In quali curriculum è inserito l'insegnamento della statistica e da quando?
L’insegnamento della statistica fin dai primi livelli di istruzione è fondamentale per garantire lo sviluppo e il sostegno della cultura “quantitativa” anche dei più piccoli. L’introduzione della statistica nei programmi di insegnamento della scuola di base italiana risale al 1979 per la scuola media (oggi scuola secondaria di primo grado) e al 1985 per la scuola elementare (oggi scuola primaria). Le indicazioni nazionali operano sull’intero territorio nazionale.
Si insegna la teoria metodologica o la lettura dei dati?
L'insegnamento prevede competenze e abilità in statistica, come padroneggiare gli strumenti (grafici e tabelle) per leggere e interpretare l’informazione quantitativa a partire dal primo ciclo di istruzione fino a tutto il secondo ciclo. Nei programmi di matematica prevale l’insegnamento delle tecniche di elaborazione dei dati con strumenti matematici; mentre i libri di testo di molte altre discipline presentano dati da “leggere” (l’esempio principale è la geografia).
Com'è recepito tale insegnamento?
Non possiamo esprimere una valutazione su come sia percepita in generale la presenza della statistica nei programmi scolastici. Ma possiamo testimoniare che le numerose iniziative Istat per insegnanti e allievi trovano sempre un'ottima accoglienza da parte delle scuole. Ogni anno sono centinaia le scuole con cui collaboriamo e migliaia le persone giovani che “sperimentano” la statistica in classe insieme all’Istat: testimoniano soddisfazione e desiderio di approfondire.
Le Olimpiadi di Statistica quando sono state lanciate? Quante persone partecipano?
Nell’anno scolastico 2021-22 si è svolta la XII edizione delle Olimpiadi della Statistica. Queste, essendo rivolte alle studentesse e agli studenti delle superiori, garantiscono a chi vince la fase individuale l'iscrizione all'Albo nazionale delle Eccellenze, che è un bel premio di per sé, perché le Università abbonano le tasse di iscrizione. La fase a squadre permette invece a chi vince di partecipare alle Olimpiadi europee, decisamente più orientate alla conoscenza dei dati di statistica ufficiale prodotti dai vari Istituti nazionali di statistica e da Eurostat, che non alla parte teorica. Alle Olimpiadi europee partecipano 17 Paesi. Quest’anno su un totale (ancora non definitivo) di 16.507 iscritti complessivi, la quota proveniente dall’Italia è di 5.195 persone. Quelle effettivamente partecipanti sono state poi 4.172, per un totale di 135 scuole in tutto il territorio nazionale. Negli ultimi anni abbiamo riscontrato una notevole crescita dei licei partecipanti.
Testi consigliati per gente statisticamente arrapabile:
- David Spiegelhalter, L'arte della statistica – Cosa ci insegnano i dati, 2020, Einaudi
- David J. Hand, Statistica. Dati, numeri e l'interpretazione della realtà, 2012, Codice Edizioni- Darrell Huff, Mentire con le statistiche, 2009, Monti e Ambrosini
- Hans Rosling, Factfulness, 2018, Rizzoli
Note
1) Altraeconomia, “Il dato utile: ecco perché l’indagine statistica fa bene alle democrazie”, 1 Febbraio 2019, https://bit.ly/3ydmgxE .
2) Census Benefits Evaluation Report, 2011, https://bit.ly/3nabvpA .
3) Carl Bakker, Valuing the Census, 2014, https://bit.ly/3ndDyEI .
4) Mona Chalabi, “WEB Du Bois: retracing his attempt to challenge racism with data”, The Guardian, 14 febbraio 2017, https://bit.ly/3NgvQUM .
5) E. Marrese, “Statistica, la grande sconosciuta. Crea lavoro ma non attira studenti”, 23-10-2006.
6) Duffy, B. (2018). The perils of perception: Why we’re wrong about nearly everything. Atlantic Books.
7) Bickel PJ, Hjammel EA, O'Connell JW (1975) Sex Bias in Graduate Admissions: Data From Berkeley. Science, 187: 398–404.
9) Nate Con, “A 2016 Review: Why Key State Polls Were Wrong about Trump”, New York Times, 31 maggio 2017.
11) Andrew Gregory, Why going to university increases risk of getting a brain tumour, Mirror, 20 giugno 2016, https://bit.ly/3OD1GfG
12) Whitney, W. O., and C. J. Mehlhaff. "High-rise syndrome in cats." Journal of the American Veterinary Medical Association 191.11 (1987): 1399-1403.
13) Diamond, Jared M. "Why cats have nine lives." Nature 332.6165 (1988): 586-587.
14) Taleb, Nassim N. Il cigno nero. Come l'improbabile governa la nostra vita. Il Saggiatore, 2009.
15) K. Pearson, The Life, Letters and Labours for Francis Galton, vol. 2, 1924.
16) Alberto Cairo, Come i grafici mentono. Capire meglio le informazioni visive, Raffaello Cortina Editore, 2020, p.67.
19) Wainer H, Zwerling HL. “Evidence That Smaller Schools Do Not Improve Student Achievement”. Phi Delta Kappan. 2006;88(4):300-303.
20) Matthews, R. (2000). Storks deliver babies (p= 0.008). Teaching Statistics, 22(2), 36-38.
22) Rossman, Allan J. "Televisions, physicians, and life expectancy." Journal of Statistics Education 2.2 (1994).
23) Sarah Boseley, “No link between MMR and autism, major study concludes”, The Guardian, 21 aprile 2015, https://bit.ly/3I2jJdf
24) AIRC, “DreamLab: un’app per esplorare l'ecosistema tumorale”, 17 settembre 2021, https://bit.ly/2KkLSky
27) Per esempio il Los Angeles Times: https://lat.ms/3OmYwNh
28) D. Randall, “Giocare con i numeri” in Internazionale, 597, 1 luglio 2005, p. 17.
29) Sumner, Petroc, et al. "The association between exaggeration in health related science news and academic press releases: retrospective observational study." Bmj 349 (2014).
30) M. Schield, Statistical prevarication, in Statistical education and communication, Atti della Conferenza dell’associazione internazionale per l’educazione statistica, Sidney, 4-5 aprile 2005, p.1.
31) Templer, Donald I., David M. Veleber, and Robert K. Brooner. "Geophysical variables and behavior: VI. Lunar phase and accident injuries: A difference between night and day." Perceptual and Motor Skills 55.1 (1982): 280-282.
32) Simmons JP, Nelson LD, Simonsohn U. False-Positive Psychology: Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant. Psychological Science. 2011;22(11):1359-1366.
33) Cochrane, A. L. (1984). “Sickness in Salonica: my first, worst, and most successful clinical trial”. British medical journal (Clinical research ed.), 289(6460), 1726.
34) Charles Duhigg, “How Companies Learn Your Secrets”, New York Times, 19 febbraio 2012.
35) Dare i numeri. Dieci regole per capire come interpretare i dati, Tim Hardford.
36) Faravelli, E., Mazur, J. (2017). Travolti dal caso. Matematica e mitologie delle coincidenze. Il Saggiatore.
38) Tversky, Amos, and Daniel Kahneman. "Judgment under Uncertainty: Heuristics and Biases: Biases in judgments reveal some heuristics of thinking under uncertainty", Science 185.4157 (1974): 1124-1131.
39) Fisher RA: Smoking, the Cancer Controversy: Some Attempts to Assess the Evidence. Edinburgh, Oliver and Boyd, 1959.