Un modo semplice e abbastanza sicuro per classificare gli appartenenti a un qualunque gruppo di abitanti degli Stati Uniti in una delle tre categorie repubblicani, democratici e nerd è raccontare una delle tante varianti dell’aneddoto secondo il quale il Presidente degli Stati Uniti George W. Bush si sarebbe stupito del fatto che «metà degli americani ha un’intelligenza al di sotto della media».
I democratici faranno gli spiritosi sull’intelligenza dello stesso George W.; i repubblicani si lamenteranno degli intellettuali liberal che fanno queste battute saccenti e i nerd osserveranno come in realtà l’osservazione funziona se si usa la mediana invece della media, oppure se la distribuzione è simmetrica (l’esperienza insegna che i lettori di questa rubrica sono quasi tutti nel terzo gruppo, quindi forse quello che segue è poco utile, ma tant’è).
Ci eravamo proposti di parlare di statistica, cominceremo quindi dalle basi: che cosa vuol dire, per esempio, che una persona è “mediamente intelligente”?
Più o meno tutti sanno come si calcola la media di un insieme di numeri, per esempio i voti ottenuti da uno studente: si sommano tutti i valori, si divide per quanti sono i voti e si ottiene un numero che riassume il tutto. È semplice, comodo e utile per molte cose, ma a volte non basta. Per esempio, Berlino e Londra hanno la stessa temperatura media nell’anno (10.3°C), ma la differenza tra inverno ed estate è molto più marcata a Berlino, dove la temperatura media in agosto è 20.3°C e quella in gennaio 0.6°C, mentre a Londra i valori sono molto più vicini: 17.4°C e 4.3°C; il clima è dunque abbastanza diverso e la sola temperatura media mi dà troppo poca informazione per decidere che vestiti portare a Londra o a Berlino, e infatti nei bollettini meteorologici si indicano generalmente le temperature minime e massime.
In molte circostanze è quindi utile non solo conoscere il valore medio, ma anche avere un’idea di quanto i valori si discostino da esso. Abbiamo appena visto che un modo un po’ rudimentale come indicare gli estremi della variabilità in alcuni casi è sufficiente, ma esiste un modo più rigoroso di cui abbiamo parlato in uno dei primi numeri di questa rubrica, ormai molti anni fa. La deviazione standard (o “scarto quadratico medio”), spesso indicata con la lettera greca sigma, indica proprio quanto i valori sono sparpagliati intorno alla media: più è grande sigma più valori ci sono anche molto lontani dalla media, e viceversa. La formula per calcolare la deviazione standard è appena più complicata di quella per la media, non la scriviamo qui ma si trova molto facilmente[1].
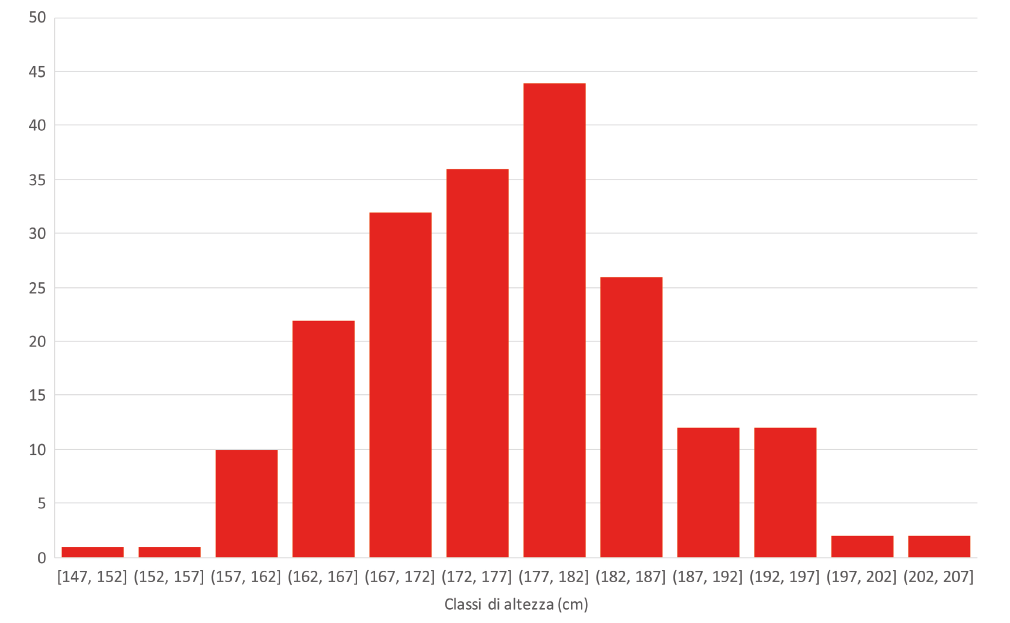
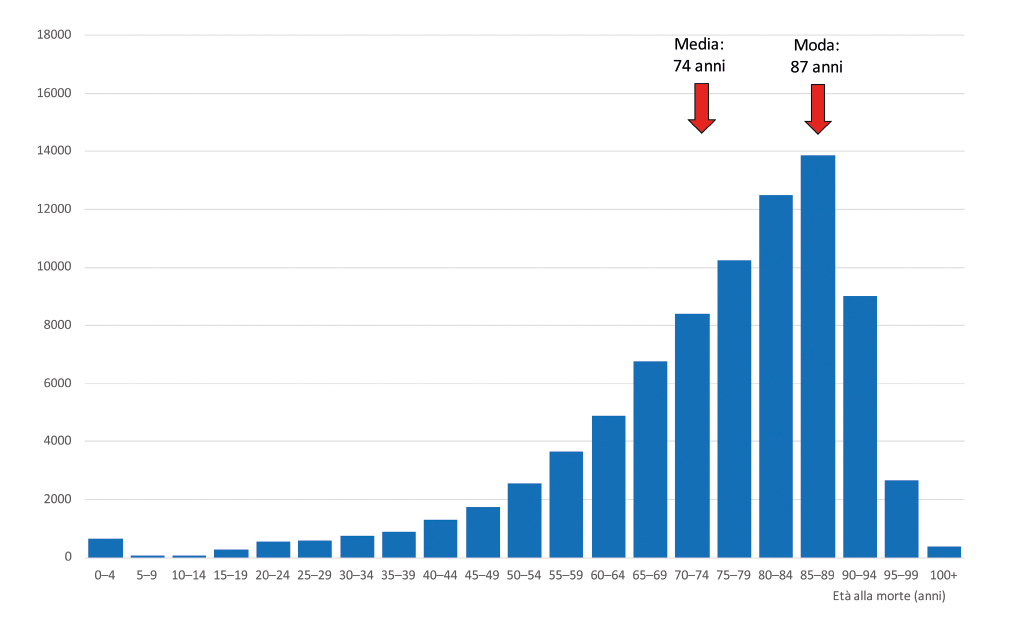
A volte però anche le informazioni fornite da media e deviazione standard non sono sufficienti, e abbiamo bisogno di qualcosa di più per capire come stanno le cose. Complichiamo un po’ le cose usando un istogramma, un tipo di grafico a barre in cui ogni colonna corrisponde a una “classe” e la sua altezza a quanti casi rientrano in quella classe. Per esempio, se misuro l’altezza di un gruppo di persone posso poi raggrupparle in “classi” come nell’istogramma di figura 1: la prima colonna corrisponde alle altezze tra 140 e 145 cm, la seconda tra 145 e 150 cm eccetera[2]. In questo caso i valori si distribuiscono intorno alla media come la famosa “curva a campana” della distribuzione di Gauss, e abbiamo spesso l’idea che sia sempre così. In realtà non è per niente vero, e per capirlo usiamo dei dati reali: l’età alla morte degli uomini australiani nel 2016[3]. L’età media alla morte è circa 74 anni, ma il grafico in figura 2 racconta una storia molto più interessante. La distribuzione è fortemente asimmetrica, e la media ci dice poco: ci sono tantissimi che muoiono in età ben più avanzata di 74 anni. In questo caso per “riassumere” i dati in maniera utile si può usare la mediana della distribuzione, ossia il valore che “taglia a metà” la distribuzione: ci sono tanti casi a sinistra della mediana quanti a destra; la mediana è quindi 78 anni. In questo caso forse ancora più interessante è la moda, cioè il valore più frequente; che qui corrisponde alla classe 85-89 anni. 
Anche se è vero che l’età media alla morte è 74 anni, questo dato si rivela poco informativo: in realtà la maggior parte degli australiani muore intorno a 87 anni.
Questo significa che è automaticamente vero che metà degli americani ha l’intelligenza più bassa della mediana. Se poi la distribuzione è simmetrica (ma non lo sappiamo), media e mediana coincidono e la frase attribuita a George W. Bush si rivela essere proprio vera. Se volessimo quindi trarne una morale, potremmo concludere che è bene diffidare delle espressioni generiche come “mediamente”.
I democratici faranno gli spiritosi sull’intelligenza dello stesso George W.; i repubblicani si lamenteranno degli intellettuali liberal che fanno queste battute saccenti e i nerd osserveranno come in realtà l’osservazione funziona se si usa la mediana invece della media, oppure se la distribuzione è simmetrica (l’esperienza insegna che i lettori di questa rubrica sono quasi tutti nel terzo gruppo, quindi forse quello che segue è poco utile, ma tant’è).
Ci eravamo proposti di parlare di statistica, cominceremo quindi dalle basi: che cosa vuol dire, per esempio, che una persona è “mediamente intelligente”?
Più o meno tutti sanno come si calcola la media di un insieme di numeri, per esempio i voti ottenuti da uno studente: si sommano tutti i valori, si divide per quanti sono i voti e si ottiene un numero che riassume il tutto. È semplice, comodo e utile per molte cose, ma a volte non basta. Per esempio, Berlino e Londra hanno la stessa temperatura media nell’anno (10.3°C), ma la differenza tra inverno ed estate è molto più marcata a Berlino, dove la temperatura media in agosto è 20.3°C e quella in gennaio 0.6°C, mentre a Londra i valori sono molto più vicini: 17.4°C e 4.3°C; il clima è dunque abbastanza diverso e la sola temperatura media mi dà troppo poca informazione per decidere che vestiti portare a Londra o a Berlino, e infatti nei bollettini meteorologici si indicano generalmente le temperature minime e massime.
In molte circostanze è quindi utile non solo conoscere il valore medio, ma anche avere un’idea di quanto i valori si discostino da esso. Abbiamo appena visto che un modo un po’ rudimentale come indicare gli estremi della variabilità in alcuni casi è sufficiente, ma esiste un modo più rigoroso di cui abbiamo parlato in uno dei primi numeri di questa rubrica, ormai molti anni fa. La deviazione standard (o “scarto quadratico medio”), spesso indicata con la lettera greca sigma, indica proprio quanto i valori sono sparpagliati intorno alla media: più è grande sigma più valori ci sono anche molto lontani dalla media, e viceversa. La formula per calcolare la deviazione standard è appena più complicata di quella per la media, non la scriviamo qui ma si trova molto facilmente[1].
Figura 1. Distribuzione dell’altezza in un gruppo di 400 persone.
Figura 2. Distribuzione dell’età alla morte degli uomini australiani maschi nel 2016.
Anche se è vero che l’età media alla morte è 74 anni, questo dato si rivela poco informativo: in realtà la maggior parte degli australiani muore intorno a 87 anni.
Questo significa che è automaticamente vero che metà degli americani ha l’intelligenza più bassa della mediana. Se poi la distribuzione è simmetrica (ma non lo sappiamo), media e mediana coincidono e la frase attribuita a George W. Bush si rivela essere proprio vera. Se volessimo quindi trarne una morale, potremmo concludere che è bene diffidare delle espressioni generiche come “mediamente”.
Note
1) Per esempio su Wikipedia: https://bit.ly/2SaYevN
2) Per i più curiosi, la media e la deviazione standard dei dati in figura 1 sono rispettivamente 178cm e 10cm, che corrispondono agli americani maschi adulti.
