Si racconta che Enrico Fermi fosse solito porre ai propri studenti strane domande come “Quanti sono gli accordatori di pianoforte a Chicago?”
Fermi ovviamente non era interessato a sapere il numero esatto dei professionisti in grado di restituire ad un pianoforte la sua corretta funzionalità.
Al grande fisico romano importava invece sviluppare nei suoi studenti le capacità di ragionamento utili a risolvere i problemi che si trovano ad affrontare tutti gli scienziati nel loro lavoro di ricerca.
Uno dei primi strumenti di un’immaginaria cassetta degli attrezzi di uno scienziato (sia esso matematico, fisico, chimico, ingegnere, ecc...) è proprio la capacità di stimare l’ordine di grandezza del fenomeno che si dovrà studiare.
Una battuta che gira fra gli scienziati (non è chiaro a chi sia attribuibile) è infatti: “Uno scienziato non fa mai un calcolo se prima non sa quanto deve risultare”. In altri termini, qualunque problema di tipo quantitativo si stia affrontando ci si chiede, prima ancora di trovare la risposta, se si è in grado di stimarne l’ordine di grandezza. Ovvero se il valore che ci si aspetta di trovare è 10, 100 o 100000.
Nel caso degli accordatori di pianoforte la cosa non è così importante, ma immaginate di dover progettare un costoso esperimento per indagare qualcosa di mai osservato. Se non si sono formulate delle ipotesi stringenti sull’ordine di grandezza del valore atteso, sarebbe impossibile (o semplicemente molto costoso) realizzare l’esperimento.
In rete si possono trovare tanti esempi di questo tipo di problemi (cfr[1]). Esiste anche un sito web di un’università che ha realizzato una raccolta di questa tipologia di quesiti (cfr. [2]). Alcuni esempi:
- Quanti capelli ha in testa una persona?
- Quanti spaghetti ci sono in un kg di pasta?
- Quante palline da pingpong entrano nella vostra cucina?
- Quanto è l’ammontare mensile di euro necessario per pagare le pensioni a tutti i pensionati italiani?
I lettori di questa rivista conosceranno già alcuni di questi problemi e avranno chiaro che non si cerca la risposta esatta ma solo l’ordine di grandezza.
Per esempio, per rispondere alla domanda circa gli accordatori di pianoforte si può dire che l’ordine di grandezza gli abitanti di Chicago è circa 10^6 e che in media c’è circa 1 pianoforte ogni 100 persone. Inoltre, possiamo pensare che un accordatore in un anno accordi circa 10^2 pianoforti. Si giunge quindi alla stima di circa 10^2 accordatori di pianoforte.
Se volessimo, invece, stimare l’ordine di grandezza di quanti capelli ha in testa una persona (escludendo ovviamente i calvi) si potrebbe valutare la superficie della nostra testa (una mezza sfera) e moltiplicare questo valore per una stima approssimativa dei capelli presenti per mm^2.
Anche se per affrontare questi quesiti sono necessarie solo conoscenze relative ad operazioni come moltiplicazione e divisione e un po’ di buon senso per fare delle stime, vedremo che queste competenze non sono affatto scontate.
In effetti, anche chi viene da una formazione scientifica, se non allenato a questo tipo di ragionamento, può incorrere in errori non da poco nel rispondere a domande meno banali di quelle indicate sopra.
Tutti noi, senza una adeguata attenzione e un allenamento in questa tipologia di ragionamenti, abbiamo difficoltà a “rappresentare” nella nostra testa numeri troppo piccoli o numeri troppo grandi e di conseguenza non sempre riusciamo a fare stime corrette.
Nel campo della didattica, (cfr [3],[4]) l’insistere sull’importanza della stima dell’ordine di grandezza è ormai parte integrante della prassi pedagogica dell’insegnamento di materie come matematica, fisica, chimica.
La ricerca ha evidenziato come errori derivanti da quello che in letteratura è indicato come “senso nel numero” è una problematica comune in molti studenti.
Anche le proprietà delle potenze, un bagaglio di conoscenze che si apprendono a livello di scuola secondaria di primo grado (la scuola media), non sempre sono diffusamente note. Per questo motivo, una gran parte dei libri, soprattutto di fisica, riportano esempi di problemi in cui si chiede di stimare l’ordine di grandezza con domande analoghe agli esempi precedentemente riportati.
Nonostante questo, il problema è fare in modo che questa conoscenza appresa diventi davvero una “competenza” che un futuro cittadino sia in grado di utilizzare nella vita di tutti i giorni.
Uno degli strumenti più utilizzati dagli oratori (politici, giornalisti e opinionisti vari) è quello di sfoderare una lista di numeri e statistiche a sostegno delle loro tesi e affiancare, a questi numeri, proposte di modifiche di leggi o quanto altro. Anche molte delle fake news che girano su internet sono solite citare numeri e statistiche a loro vantaggio.
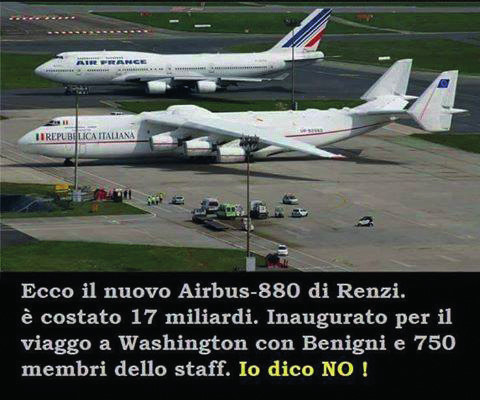
Un esempio recente è quello del presunto costo di un aereo acquistato dal governo italiano. In rete girava un’immagine che conteneva una serie di informazioni false. La prima cosa che dovrebbe essere evidente è che l’ordine di grandezza del costo di un velivolo, per quanto grande e lussuoso, non può essere pari al valore di una finanziaria italiana (cfr [5]).
Eppure, la notizia è stata condivisa da molti utenti. A prescindere dall’opinione politica di chi ci sta leggendo e dall’opportunità o meno di intraprendere una procedura di leasing per un aereo di stato, è evidente che il costo, anche in caso di acquisto, non poteva essere quello della cifra riportata.
Un altro esempio classico di problema di stima dell’ordine di grandezza è quello del numero dei partecipanti ad una manifestazione e del differente valore dato da organizzatori e questura.
Ad ogni manifestazione si ripete puntualmente un balletto di numeri che spesso differiscono di un fattore 10 fra loro.
È possibile credere alla notizia secondo cui in una piazza sono entrati 2-3 milioni di persone quando, stimando l’estensione in metri quadrati della stessa e mettendo i partecipanti stipati come sardine, si arriva al massimo a duecento-trecentomila persone ovvero un ordine di grandezza inferiore?
Per esempio, la storica piazza San Giovanni di Roma, luogo tradizionalmente adibito a manifestazioni e concerti, ha una estensione di circa 40.000 metri quadrati e, anche ipotizzando una presenza in media elevata di 5-6 persone a metro quadrato, non è possibile arrivare al milione di partecipanti, neanche coinvolgendo le zone limitrofe dove inevitabilmente la densità dei manifestanti sarà di gran lunga più bassa.
Un ulteriore esempio è rappresentato dalle proposte (alcune ormai attuate) di abolizione di alcune spese della politica (per esempio i vitalizi dei parlamentari).
È in grado un elettore di stimare l’ordine di grandezza di questi risparmi?
Di fronte a queste difficoltà si conferma, invece, l’importanza di imparare a risolvere questi cosiddetti “problemi alla Fermi”. Questa competenza dovrebbe entrare a far parte del bagaglio di conoscenze di ogni cittadino che in questo modo sarebbe in possesso di un utile “setaccio” per selezionare le affermazioni non veritiere.
Fermi ovviamente non era interessato a sapere il numero esatto dei professionisti in grado di restituire ad un pianoforte la sua corretta funzionalità.
Al grande fisico romano importava invece sviluppare nei suoi studenti le capacità di ragionamento utili a risolvere i problemi che si trovano ad affrontare tutti gli scienziati nel loro lavoro di ricerca.
Uno dei primi strumenti di un’immaginaria cassetta degli attrezzi di uno scienziato (sia esso matematico, fisico, chimico, ingegnere, ecc...) è proprio la capacità di stimare l’ordine di grandezza del fenomeno che si dovrà studiare.
Una battuta che gira fra gli scienziati (non è chiaro a chi sia attribuibile) è infatti: “Uno scienziato non fa mai un calcolo se prima non sa quanto deve risultare”. In altri termini, qualunque problema di tipo quantitativo si stia affrontando ci si chiede, prima ancora di trovare la risposta, se si è in grado di stimarne l’ordine di grandezza. Ovvero se il valore che ci si aspetta di trovare è 10, 100 o 100000.
Nel caso degli accordatori di pianoforte la cosa non è così importante, ma immaginate di dover progettare un costoso esperimento per indagare qualcosa di mai osservato. Se non si sono formulate delle ipotesi stringenti sull’ordine di grandezza del valore atteso, sarebbe impossibile (o semplicemente molto costoso) realizzare l’esperimento.
Immagine della fake news sul presunto aereo acquistato dal gove rno italiano per la non verosimile cifra di 17 miliardi corrispondente all’importo di una finanziaria italiana.
Qualche esempio di “Problemi alla Fermi”
In rete si possono trovare tanti esempi di questo tipo di problemi (cfr[1]). Esiste anche un sito web di un’università che ha realizzato una raccolta di questa tipologia di quesiti (cfr. [2]). Alcuni esempi:
- Quanti capelli ha in testa una persona?
- Quanti spaghetti ci sono in un kg di pasta?
- Quante palline da pingpong entrano nella vostra cucina?
- Quanto è l’ammontare mensile di euro necessario per pagare le pensioni a tutti i pensionati italiani?
I lettori di questa rivista conosceranno già alcuni di questi problemi e avranno chiaro che non si cerca la risposta esatta ma solo l’ordine di grandezza.
Per esempio, per rispondere alla domanda circa gli accordatori di pianoforte si può dire che l’ordine di grandezza gli abitanti di Chicago è circa 10^6 e che in media c’è circa 1 pianoforte ogni 100 persone. Inoltre, possiamo pensare che un accordatore in un anno accordi circa 10^2 pianoforti. Si giunge quindi alla stima di circa 10^2 accordatori di pianoforte.
Se volessimo, invece, stimare l’ordine di grandezza di quanti capelli ha in testa una persona (escludendo ovviamente i calvi) si potrebbe valutare la superficie della nostra testa (una mezza sfera) e moltiplicare questo valore per una stima approssimativa dei capelli presenti per mm^2.
Anche se per affrontare questi quesiti sono necessarie solo conoscenze relative ad operazioni come moltiplicazione e divisione e un po’ di buon senso per fare delle stime, vedremo che queste competenze non sono affatto scontate.
In effetti, anche chi viene da una formazione scientifica, se non allenato a questo tipo di ragionamento, può incorrere in errori non da poco nel rispondere a domande meno banali di quelle indicate sopra.
Le cose sono meno semplici di quello che sembrano
Tutti noi, senza una adeguata attenzione e un allenamento in questa tipologia di ragionamenti, abbiamo difficoltà a “rappresentare” nella nostra testa numeri troppo piccoli o numeri troppo grandi e di conseguenza non sempre riusciamo a fare stime corrette.
Nel campo della didattica, (cfr [3],[4]) l’insistere sull’importanza della stima dell’ordine di grandezza è ormai parte integrante della prassi pedagogica dell’insegnamento di materie come matematica, fisica, chimica.
La ricerca ha evidenziato come errori derivanti da quello che in letteratura è indicato come “senso nel numero” è una problematica comune in molti studenti.
Anche le proprietà delle potenze, un bagaglio di conoscenze che si apprendono a livello di scuola secondaria di primo grado (la scuola media), non sempre sono diffusamente note. Per questo motivo, una gran parte dei libri, soprattutto di fisica, riportano esempi di problemi in cui si chiede di stimare l’ordine di grandezza con domande analoghe agli esempi precedentemente riportati.
Nonostante questo, il problema è fare in modo che questa conoscenza appresa diventi davvero una “competenza” che un futuro cittadino sia in grado di utilizzare nella vita di tutti i giorni.
L’ordine di grandezza come strumento di debunking
Uno degli strumenti più utilizzati dagli oratori (politici, giornalisti e opinionisti vari) è quello di sfoderare una lista di numeri e statistiche a sostegno delle loro tesi e affiancare, a questi numeri, proposte di modifiche di leggi o quanto altro. Anche molte delle fake news che girano su internet sono solite citare numeri e statistiche a loro vantaggio.
Un esempio recente è quello del presunto costo di un aereo acquistato dal governo italiano. In rete girava un’immagine che conteneva una serie di informazioni false. La prima cosa che dovrebbe essere evidente è che l’ordine di grandezza del costo di un velivolo, per quanto grande e lussuoso, non può essere pari al valore di una finanziaria italiana (cfr [5]).
Eppure, la notizia è stata condivisa da molti utenti. A prescindere dall’opinione politica di chi ci sta leggendo e dall’opportunità o meno di intraprendere una procedura di leasing per un aereo di stato, è evidente che il costo, anche in caso di acquisto, non poteva essere quello della cifra riportata.
Un altro esempio classico di problema di stima dell’ordine di grandezza è quello del numero dei partecipanti ad una manifestazione e del differente valore dato da organizzatori e questura.
Ad ogni manifestazione si ripete puntualmente un balletto di numeri che spesso differiscono di un fattore 10 fra loro.
È possibile credere alla notizia secondo cui in una piazza sono entrati 2-3 milioni di persone quando, stimando l’estensione in metri quadrati della stessa e mettendo i partecipanti stipati come sardine, si arriva al massimo a duecento-trecentomila persone ovvero un ordine di grandezza inferiore?
Un momento di uno dei concerti del Primo Maggio che si svolgono da tradizione nella piazza di San Giovanni di Roma
Un ulteriore esempio è rappresentato dalle proposte (alcune ormai attuate) di abolizione di alcune spese della politica (per esempio i vitalizi dei parlamentari).
È in grado un elettore di stimare l’ordine di grandezza di questi risparmi?
Di fronte a queste difficoltà si conferma, invece, l’importanza di imparare a risolvere questi cosiddetti “problemi alla Fermi”. Questa competenza dovrebbe entrare a far parte del bagaglio di conoscenze di ogni cittadino che in questo modo sarebbe in possesso di un utile “setaccio” per selezionare le affermazioni non veritiere.
Riferimenti bibliografici
1) Video illustrativo dei problemi alla Fermi realizzato dal Ted (Technology Entertainment Design) Education be/0YzvupOX8Is
2) Sito dell’università del Maryland dedicato ai problemi alla Fermi: umd.edu/perg/fermi/fermi.htm
3) Pellegrino, C. (1999). Stima e senso del numero. In B. D’Amore & B. Jannamorelli (A cura di), Atti del IV Seminario internazionale di Didattica della Matematica di Sulmona, “Allievo, insegnante, sapere: dagli studi teorici alla pratica didattica’’, 23–24–25 aprile 1999. (p. 145-147). Sulmona: Qualevita.
4) Cricchio D., “Senso del numero, stima e controllo dei risultati in studenti di IV media”, tesi disponibile a questo indiririzzo: master/20120530_661774_MASM_Cricchio_Diana.pdf
5) Sito in cui è riportata la notizia dell’areo di stato dal costo di 17 miliardi democratica.com/focus/bufale-fake-news-pd-renzi/
