Il gioco del Monopoli è, probabilmente, il più diffuso gioco da tavolo al mondo e tutte le volte che ci avete giocato vi sarete chiesti: c’è una strategia “razionale” per massimizzare la probabilità di vittoria? La risposta è sì e ovviamente la matematica gioca un ruolo fondamentale.
Anche il lotto, il superenalotto, gratta e vinci e simili sono dei giochi molto diffusi in Italia e, analogamente, molte persone si chiedono se esista una strategia per vincere: anche qui vedremo che la matematica offre addirittura una risposta sicura e indubitabile che funziona sempre.
Partiamo subito dal secondo caso e iniziamo a definire il gioco equo. Un gioco è equo quando paga al vincitore una vincita pari all’importo giocato moltiplicato per il reciproco della probabilità di vittoria. Gratta e vinci, superenalotto, lotto e qualunque gioco di questo tipo nel frattempo sia stato inventato non lo sono.
Utilizzando la matematica è facile stabilire che questi giochi non sono equi e che l’unico che veramente “guadagna” (un accanito giocatore può “vincere”, ma non guadagnare) è solo il “banco”, ovvero chi li gestisce.
Se per esempio il lotto fosse un gioco equo, chi indovina un ambo dovrebbe incassare circa 400 volte la posta e invece vince 250 volte la somma scommessa, e così per le altre possibilità.
La strategia per vincere sempre è quindi chiara: farsi dare il gioco in gestione dallo Stato.
Esiste in realtà anche un’altra strategia, chiara e certa, che almeno garantisce di non perdere: non giocare.
Tutto il resto non ha fondamento matematico. Numeri ritardatari, numeri gemelli, numeri spia e strategie simili non hanno nessun fondamento. Al grande matematico Bruno de Finetti si attribuisce la seguente affermazione, che può essere estesa a tutti i giochi d’azzardo gestiti da un monopolio di Stato: il lotto è “la tassa sull'imbecillità”.
Dal punto di vista sociale sarebbe interessante riflettere sul fatto che lo Stato (e chi ne gestisce il monopolio) guadagna non poco con questi giochi, però questa tipologia di scommesse crea una forte dipendenza che, in alcuni casi, diventa una vera e propria patologia, il cui costo ricade sullo Stato medesimo.
Il Politecnico di Milano ha intrapreso una lodevole attività per sensibilizzare i giovani sulla problematica delle scommesse chiamata Bet on math ovvero scommetti sulla matematica e scopri che non vale la pena scommettere nel gioco d’azzardo.
Avendo chiaro che questa tipologia di giochi non ha senso, possiamo quindi concentrarci a giocare in modo spensierato al Monopoli, dove i soldi sono finti ma la soddisfazione di battere amici e parenti è impagabile.
In questo caso nessuno finisce sul lastrico e al massimo finiscono delle amicizie per eccesso di cattiveria.
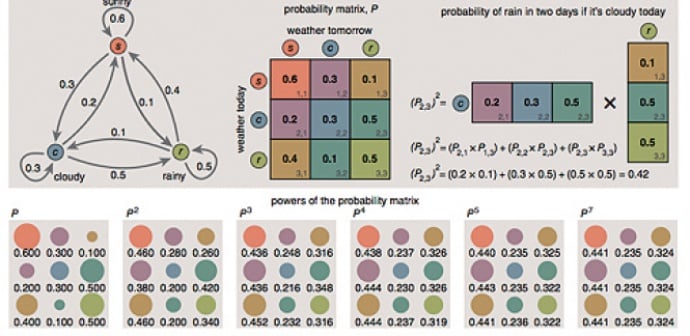
Si deve al grande matematico russo Andrey Markov la creazione di quelle che oggi sono conosciute come le catene di Markov con le quali è possibile modellizzare molti fenomeni, usando un approccio probabilistico.
Nell’accezione più semplice, si tratta di sistemi con un numero finito di stati in cui la transizione da uno stato all'altro avviene su base probabilistica. In altre parole, l’informazione disponibile circa una catena al generico istante t è fornita dalle probabilità che essa si trovi in uno qualsiasi degli stati, e l'evoluzione temporale della catena viene specificata precisando in qual modo tali probabilità si aggiornino passando dall'istante t all’istante t+ 1. Questa affermazione è simile a quella che si fa in fisica quando si dice che posso determinare la posizione di un corpo fra un secondo conoscendo semplicemente le condizioni attuali e trascurando dove stava lo stesso corpo negli istanti precedenti. La trattazione delle catene di Markov può ricondursi allora a quella di sistemi il cui comportamento nel tempo è rappresentato da vettori, ovvero una lista ordinata di numeri, che contengono la probabilità dei possibili stati.
Nella figura 1 è presentata un’immagine che illustra l’esempio di un “mondo fantastico” in cui esistono solo tre possibili condizioni del tempo: sole, nuvole, pioggia (in figura rappresentate con le lettere (s) per sunny, (c) per cloudy e (r) per rainy) e di come è possibile ottenere la probabilità che fra due giorni piova sapendo che il giorno prima sia stato nuvoloso.
Nel caso del Monopoli la mia posizione è influenzata in modo esaustivo dal lancio precedente e può quindi essere applicato il modello di Markov, solo che gli stati possibili sono le 40 caselle che diventano molti di più se si considerano le complicazioni generate dalla tanto odiata casella prigione.
Utilizzando questo modello è possibile estrapolare una modalità di gioco ottimale che massimizza la probabilità di vittoria.
Senza andare troppo nel dettaglio illustriamo alcuni semplici strategie che si possono usare.
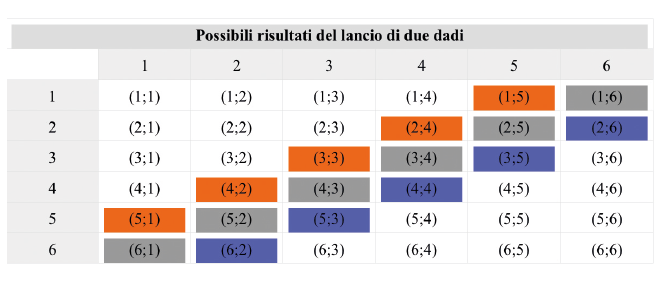
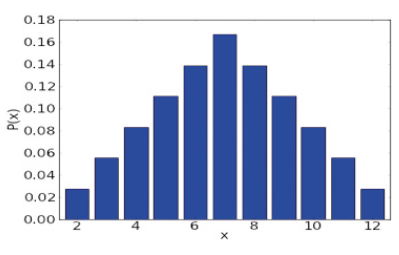Dato che a Monopoli si lanciano due dadi, il risultato più probabile è 7 (seguito a breve distanza da 6 e 8).
Le caselle che distano dall'inizio del gioco multipli di questi numeri saranno quelle in cui è più probabile andare a finire e quindi sono quelle che conviene acquistare e edificare.
Altra casella fondamentale è quella della prigione. In base alle regole del Monopoli, finire nella casella prigione è più probabile che capitare in altri luoghi. È quindi una mossa vantaggiosa comprare i terreni posizionati dopo la prigione poiché è facile che i vostri avversari ci finiscano.
Si dimostra, inoltre, che la strategia migliore è quella di edificare più case possibili appena possibile, in modo da massimizzare in breve tempo i guadagni.
Infine, dovendo scegliere da quale investimento partire, il suggerimento è quello di investire da subito nelle stazioni perché costano poco e sono tra i luoghi in cui è più facile capitare.
L’elenco dei suggerimenti non finisce qui. Per scoprirli tutti vi rimandiamo alla bibliografia, certi di avervi incuriosito.
Anche il lotto, il superenalotto, gratta e vinci e simili sono dei giochi molto diffusi in Italia e, analogamente, molte persone si chiedono se esista una strategia per vincere: anche qui vedremo che la matematica offre addirittura una risposta sicura e indubitabile che funziona sempre.
Partiamo subito dal secondo caso e iniziamo a definire il gioco equo. Un gioco è equo quando paga al vincitore una vincita pari all’importo giocato moltiplicato per il reciproco della probabilità di vittoria. Gratta e vinci, superenalotto, lotto e qualunque gioco di questo tipo nel frattempo sia stato inventato non lo sono.
Utilizzando la matematica è facile stabilire che questi giochi non sono equi e che l’unico che veramente “guadagna” (un accanito giocatore può “vincere”, ma non guadagnare) è solo il “banco”, ovvero chi li gestisce.
Se per esempio il lotto fosse un gioco equo, chi indovina un ambo dovrebbe incassare circa 400 volte la posta e invece vince 250 volte la somma scommessa, e così per le altre possibilità.
La strategia per vincere sempre è quindi chiara: farsi dare il gioco in gestione dallo Stato.
Esiste in realtà anche un’altra strategia, chiara e certa, che almeno garantisce di non perdere: non giocare.
Tutto il resto non ha fondamento matematico. Numeri ritardatari, numeri gemelli, numeri spia e strategie simili non hanno nessun fondamento. Al grande matematico Bruno de Finetti si attribuisce la seguente affermazione, che può essere estesa a tutti i giochi d’azzardo gestiti da un monopolio di Stato: il lotto è “la tassa sull'imbecillità”.
Dal punto di vista sociale sarebbe interessante riflettere sul fatto che lo Stato (e chi ne gestisce il monopolio) guadagna non poco con questi giochi, però questa tipologia di scommesse crea una forte dipendenza che, in alcuni casi, diventa una vera e propria patologia, il cui costo ricade sullo Stato medesimo.
Il Politecnico di Milano ha intrapreso una lodevole attività per sensibilizzare i giovani sulla problematica delle scommesse chiamata Bet on math ovvero scommetti sulla matematica e scopri che non vale la pena scommettere nel gioco d’azzardo.
Avendo chiaro che questa tipologia di giochi non ha senso, possiamo quindi concentrarci a giocare in modo spensierato al Monopoli, dove i soldi sono finti ma la soddisfazione di battere amici e parenti è impagabile.
In questo caso nessuno finisce sul lastrico e al massimo finiscono delle amicizie per eccesso di cattiveria.
Si deve al grande matematico russo Andrey Markov la creazione di quelle che oggi sono conosciute come le catene di Markov con le quali è possibile modellizzare molti fenomeni, usando un approccio probabilistico.
Nell’accezione più semplice, si tratta di sistemi con un numero finito di stati in cui la transizione da uno stato all'altro avviene su base probabilistica. In altre parole, l’informazione disponibile circa una catena al generico istante t è fornita dalle probabilità che essa si trovi in uno qualsiasi degli stati, e l'evoluzione temporale della catena viene specificata precisando in qual modo tali probabilità si aggiornino passando dall'istante t all’istante t+ 1. Questa affermazione è simile a quella che si fa in fisica quando si dice che posso determinare la posizione di un corpo fra un secondo conoscendo semplicemente le condizioni attuali e trascurando dove stava lo stesso corpo negli istanti precedenti. La trattazione delle catene di Markov può ricondursi allora a quella di sistemi il cui comportamento nel tempo è rappresentato da vettori, ovvero una lista ordinata di numeri, che contengono la probabilità dei possibili stati.
Tabella 1: tutti i possibili casi che si possono ottenere lanciando due dadi. In grigio sono inseriti le possibili combinazioni che danno come somma 7 (6 su 36), in arancione quelle che danno 6 (5 su 36) e 8 in azzurro (5 su 36).
Nel caso del Monopoli la mia posizione è influenzata in modo esaustivo dal lancio precedente e può quindi essere applicato il modello di Markov, solo che gli stati possibili sono le 40 caselle che diventano molti di più se si considerano le complicazioni generate dalla tanto odiata casella prigione.
Utilizzando questo modello è possibile estrapolare una modalità di gioco ottimale che massimizza la probabilità di vittoria.
Senza andare troppo nel dettaglio illustriamo alcuni semplici strategie che si possono usare.
Figura 2: Istogramma della probabilità dei risultati che si ottengono lanciando due dadi. Dall'istogramma si osserva che il risultato più probabile è 7 mentre 2 e 12 quelli meno probabili.
Le caselle che distano dall'inizio del gioco multipli di questi numeri saranno quelle in cui è più probabile andare a finire e quindi sono quelle che conviene acquistare e edificare.
Altra casella fondamentale è quella della prigione. In base alle regole del Monopoli, finire nella casella prigione è più probabile che capitare in altri luoghi. È quindi una mossa vantaggiosa comprare i terreni posizionati dopo la prigione poiché è facile che i vostri avversari ci finiscano.
Si dimostra, inoltre, che la strategia migliore è quella di edificare più case possibili appena possibile, in modo da massimizzare in breve tempo i guadagni.
Infine, dovendo scegliere da quale investimento partire, il suggerimento è quello di investire da subito nelle stazioni perché costano poco e sono tra i luoghi in cui è più facile capitare.
L’elenco dei suggerimenti non finisce qui. Per scoprirli tutti vi rimandiamo alla bibliografia, certi di avervi incuriosito.
Riferimenti bibliografici
- Brian Hayes, “First Links in the Markov Chain”, American Scientist, Volume 101 Computing Science
- Il progetto “Bet on math” del Politecnico di Milano: http://betonmath.polimi.it/
- Dati ufficiali delle probabilità di vincita per ogni gioco: https://tinyurl.com/ydejevqq
