In questo articolo facciamo un esperimento di pensiero razionale. Immaginiamo di trovarci di fronte a un individuo che, come nel miglior stereotipo del complottista, prova a convincerci delle sue idee partendo da proclami come:
- Questo farmaco è inutile, è dannoso. È solo un modo per instaurare una dittatura sanitaria! -
- Gli investimenti nella pubblica istruzione? Soldi buttati. Studiare non paga. È un complotto di quel rettiliano di Bill Gates. -
Di fronte ad affermazioni del genere, dirette, lapidarie, che sembrano inappellabili, cosa rispondere? Forse una buona strategia è quella più semplice: non rispondere. Si fa fatica ad argomentare in queste situazioni, e la nostra parte razionale dovrebbe sapere che alla provocazione - Esistono i maiali volanti, ne sono certo. Dimostrami che non è vero - la risposta della scienza è - No, dimostrami tu che È vero. Portami i dati e io rivedrò tutte le mie convinzioni zoologiche -.
Tutt’altra storia è se, oltre ai proclami, si accompagna una frase come: - Ho i numeri, posso dimostrare che è tutto vero -. In questo caso è diverso, e ha senso indagare. Presentiamo un esempio, necessariamente semplificato per fini divulgativi, che si basa su dati inventati ma realistici.
- Questo farmaco è inutile, è dannoso. È solo un modo per instaurare una dittatura sanitaria!
I dati lo dimostrano: per testare l’efficacia di questo nuovo farmaco sperimentale per la cura di una malattia piuttosto pericolosa sono stati effettuati test su 100 pazienti malati: a 50 di loro è stato somministrato il farmaco, a 50 no. Ecco i dati, presi dalle cartelle cliniche -
Eccone un estratto di 10, scelte per essere il campione più rappresentativo possibile (Ricordiamo che i dati di questo e del prossimo caso sono inventati per facilitare la comprensione della questione, ma realistici):
I dati proposti sembrerebbero dar ragione al complottista. Si consideri il primo gruppo, quello dei pazienti trattati con il farmaco: la percentuale dei guariti tra loro è del 40%, perché due su cinque sono guariti. Nel secondo gruppo, quello di controllo di cui fanno parte solo pazienti non trattati, la percentuale di guariti è decisamente più alta, il 60%, dato che tre su cinque ora stanno bene.
Il farmaco non funziona, quindi? Come muoversi?
Per rispondere è bene ricordarsi prima di tutto di richiedere la fonte dei dati, per poter controllare se sia possibile risalire a pubblicazioni scientifiche sottoposte a revisioni tra pari. Sarebbe quantomeno necessario poi che i test siano stati eseguiti e valutati correttamente, cosa non semplice in assenza di competenze specifiche. In questo caso, inoltre, leggendo l’eventuale pubblicazione si potrebbe verificare se ci sia stata una sperimentazione in doppio cieco, procedura in cui sia i soggetti esaminati, sia i somministratori del farmaco ignorano le informazioni fondamentali dell’esperimento, evitando così di influenzarne i risultati.
Immaginiamo che però il complottista abbia una risposta: - So esattamente cosa intendi e sì, l’esperimento è stato accurato e in doppio cieco, ai pazienti del secondo gruppo è stato somministrato un placebo. Come la mettiamo adesso?”
Si può certo criticare il riferimento alla dittatura sanitaria, ma i numeri sembrerebbero parlare chiaro, ha ragione lui e il farmaco addirittura peggiora le sorti dei malati.
Oppure no?
Analizziamo con più attenzione i dati delle cartelle cliniche; ci accorgiamo che non abbiamo tenuto conto di tutte le variabili in gioco, in particolare del peso dei pazienti.
- Fra i sovrappeso la percentuale dei guariti dopo la somministrazione del farmaco è del 25%, dato che una persona su quattro ora sta bene. Tutti i pazienti sovrappeso che non hanno ricevuto il farmaco sono invece deceduti.
- Fra i normopeso la situazione è analoga: tutti quelli trattati con il farmaco sono guariti, mentre “solo” il 75% dei non trattati è riuscito a cavarsela.
Considerando una variabile in più, il risultato è stato stravolto: la cura funziona. Intendiamoci, questo era un “modello giocattolo”, di soli 10 pazienti. Ce ne siamo serviti per presentare un esempio, particolarmente evidente, del paradosso statistico di Simpson[1][2], una situazione in cui una relazione tra due fenomeni appare modificata, in questo caso addirittura invertita, quando si tiene conto di variabili inizialmente ritenute superflue[3]. Siamo pronti ad affrontare il secondo proclama:
- Gli investimenti nella pubblica istruzione? Soldi buttati. Studiare non paga. È un complotto di quel rettiliano di Bill Gates.
Ho intervistato 250 persone, 140 senza diploma, 110 con diploma. 12 dei non diplomati erano disoccupati, 13 disoccupati tra i diplomati (vedi tabella sotto).
Non sarò un genio in matematica, ma 12 su 140 è meno di 13 su 110, quindi avere il diploma diminuisce la probabilità di trovare lavoro -
Cosa rispondere? Ovviamente anche stavolta chiediamo più dati, a cominciare dall’età degli intervistati. Ecco i risultati, noti qualcosa di particolare? (Vedi tabella sotto).
Di nuovo il paradosso di Simpson:
- tra gli intervistati più giovani, sotto i 40 anni, il 30% (6/20) dei non diplomati è disoccupato, il 15% (12/80) dei diplomati è disoccupato;
- tra gli over 40, stesso andamento: il 5% (6/120) dei non diplomati è disoccupato, il 3,33% (1/30) dei diplomati è disoccupato.
In entrambi i casi, il diploma aiuta a trovar lavoro; il problema è piuttosto quello del tasso di disoccupazione giovanile. In figura 1 un grafico semplificato delle situazioni presentate (vedi Figura 1).
Il paradosso di Simpson si può incontrare in analisi di scienze sociali e ricerche mediche [4], il che non fa altro che sottolineare come davanti a un problema complesso non sia intellettualmente onesto accontentarsi di risposte semplici.
In generale, quindi, è bene ricordare che i dati “non parlano da soli” ma serve avere le competenze per poterli analizzare. A volte ci si può convincere, anche in buona fede, di conclusioni non corrette, perché si è data un’interpretazione che ignora alcune variabili del fenomeno.
- Questo farmaco è inutile, è dannoso. È solo un modo per instaurare una dittatura sanitaria! -
- Gli investimenti nella pubblica istruzione? Soldi buttati. Studiare non paga. È un complotto di quel rettiliano di Bill Gates. -
Di fronte ad affermazioni del genere, dirette, lapidarie, che sembrano inappellabili, cosa rispondere? Forse una buona strategia è quella più semplice: non rispondere. Si fa fatica ad argomentare in queste situazioni, e la nostra parte razionale dovrebbe sapere che alla provocazione - Esistono i maiali volanti, ne sono certo. Dimostrami che non è vero - la risposta della scienza è - No, dimostrami tu che È vero. Portami i dati e io rivedrò tutte le mie convinzioni zoologiche -.
Tutt’altra storia è se, oltre ai proclami, si accompagna una frase come: - Ho i numeri, posso dimostrare che è tutto vero -. In questo caso è diverso, e ha senso indagare. Presentiamo un esempio, necessariamente semplificato per fini divulgativi, che si basa su dati inventati ma realistici.
- Questo farmaco è inutile, è dannoso. È solo un modo per instaurare una dittatura sanitaria!
I dati lo dimostrano: per testare l’efficacia di questo nuovo farmaco sperimentale per la cura di una malattia piuttosto pericolosa sono stati effettuati test su 100 pazienti malati: a 50 di loro è stato somministrato il farmaco, a 50 no. Ecco i dati, presi dalle cartelle cliniche -
Eccone un estratto di 10, scelte per essere il campione più rappresentativo possibile (Ricordiamo che i dati di questo e del prossimo caso sono inventati per facilitare la comprensione della questione, ma realistici):
| Gruppo: trattato con farmaco Nome: Arici A. Sesso: F Età: 52 Peso: 80 kg Altezza: 1.70 m Stato: Deceduto | Gruppo: trattato con farmaco Nome: Bianchi B. Sesso: M Età: 45 Peso: 75 kg Altezza: 1.80 m Stato: Guarito | Gruppo: trattato con farmaco Nome: Cioni C. Sesso: F Età: 28 Peso: 70 kg Altezza: 1.60 m Stato: Deceduto | Gruppo: trattato con farmaco Nome: De Carli D. Sesso: M Età: 36 Peso: 95 kg Altezza: 1.80 m Stato: Guarito | Gruppo: trattato con farmaco Nome: Este E. Sesso: M Età: 54 Peso: 85 kg Altezza: 1.75 m Stato: Deceduto | Gruppo: trattato con placebo Nome: Fresco F. Sesso: M Età: 26 Peso: 80 kg Altezza: 1.65 m Stato: Deceduto | Gruppo: trattato con placebo Nome: Gala G. Sesso: F Età: 70 Peso: 50 kg Altezza: 1.65 m Stato: Guarito | Gruppo: trattato con placebo Nome: Iole I. Sesso: F Età: 31 Peso: 60 kg Altezza: 1.70 m Stato: Guarito |
| Gruppo: trattato con placebo Nome: Lodi L. Sesso: M Età: 54 Peso: 75 kg Altezza: 1.80 m Stato: Guarito | Gruppo: trattato con placebo Nome: Magli M. Sesso: F Età: 57 Peso: 50 kg Altezza: 1.60 m Stato: Deceduto |
I dati proposti sembrerebbero dar ragione al complottista. Si consideri il primo gruppo, quello dei pazienti trattati con il farmaco: la percentuale dei guariti tra loro è del 40%, perché due su cinque sono guariti. Nel secondo gruppo, quello di controllo di cui fanno parte solo pazienti non trattati, la percentuale di guariti è decisamente più alta, il 60%, dato che tre su cinque ora stanno bene.
Il farmaco non funziona, quindi? Come muoversi?
Per rispondere è bene ricordarsi prima di tutto di richiedere la fonte dei dati, per poter controllare se sia possibile risalire a pubblicazioni scientifiche sottoposte a revisioni tra pari. Sarebbe quantomeno necessario poi che i test siano stati eseguiti e valutati correttamente, cosa non semplice in assenza di competenze specifiche. In questo caso, inoltre, leggendo l’eventuale pubblicazione si potrebbe verificare se ci sia stata una sperimentazione in doppio cieco, procedura in cui sia i soggetti esaminati, sia i somministratori del farmaco ignorano le informazioni fondamentali dell’esperimento, evitando così di influenzarne i risultati.
Immaginiamo che però il complottista abbia una risposta: - So esattamente cosa intendi e sì, l’esperimento è stato accurato e in doppio cieco, ai pazienti del secondo gruppo è stato somministrato un placebo. Come la mettiamo adesso?”
Si può certo criticare il riferimento alla dittatura sanitaria, ma i numeri sembrerebbero parlare chiaro, ha ragione lui e il farmaco addirittura peggiora le sorti dei malati.
Oppure no?
Analizziamo con più attenzione i dati delle cartelle cliniche; ci accorgiamo che non abbiamo tenuto conto di tutte le variabili in gioco, in particolare del peso dei pazienti.
- Fra i sovrappeso la percentuale dei guariti dopo la somministrazione del farmaco è del 25%, dato che una persona su quattro ora sta bene. Tutti i pazienti sovrappeso che non hanno ricevuto il farmaco sono invece deceduti.
- Fra i normopeso la situazione è analoga: tutti quelli trattati con il farmaco sono guariti, mentre “solo” il 75% dei non trattati è riuscito a cavarsela.
Considerando una variabile in più, il risultato è stato stravolto: la cura funziona. Intendiamoci, questo era un “modello giocattolo”, di soli 10 pazienti. Ce ne siamo serviti per presentare un esempio, particolarmente evidente, del paradosso statistico di Simpson[1][2], una situazione in cui una relazione tra due fenomeni appare modificata, in questo caso addirittura invertita, quando si tiene conto di variabili inizialmente ritenute superflue[3]. Siamo pronti ad affrontare il secondo proclama:
- Gli investimenti nella pubblica istruzione? Soldi buttati. Studiare non paga. È un complotto di quel rettiliano di Bill Gates.
Ho intervistato 250 persone, 140 senza diploma, 110 con diploma. 12 dei non diplomati erano disoccupati, 13 disoccupati tra i diplomati (vedi tabella sotto).
Non sarò un genio in matematica, ma 12 su 140 è meno di 13 su 110, quindi avere il diploma diminuisce la probabilità di trovare lavoro -
Cosa rispondere? Ovviamente anche stavolta chiediamo più dati, a cominciare dall’età degli intervistati. Ecco i risultati, noti qualcosa di particolare? (Vedi tabella sotto).
| Intervistati totali | Senza Diploma | Con Diploma |
| 140 | 110 | |
| Disoccupati | Senza Diploma | Con Diploma |
| 12 | 13 |
| Intervistati totali | Senza Diploma | Con Diploma |
| Under 40 | 20 | 80 |
| Over 40 | 120 | 30 |
| 140 | 110 | |
| Disoccupati | Senza Diploma | Con Diploma |
| Under 40 | 6 | 12 |
| Over 40 | 6 | 1 |
| 12 | 13 | |
Di nuovo il paradosso di Simpson:
- tra gli intervistati più giovani, sotto i 40 anni, il 30% (6/20) dei non diplomati è disoccupato, il 15% (12/80) dei diplomati è disoccupato;
- tra gli over 40, stesso andamento: il 5% (6/120) dei non diplomati è disoccupato, il 3,33% (1/30) dei diplomati è disoccupato.
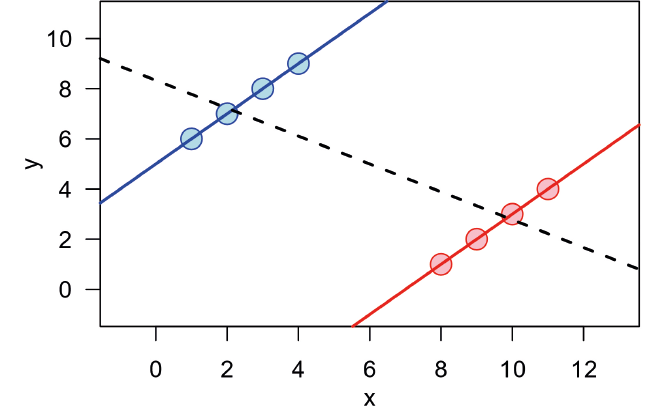
In entrambi i casi, il diploma aiuta a trovar lavoro; il problema è piuttosto quello del tasso di disoccupazione giovanile. In figura 1 un grafico semplificato delle situazioni presentate (vedi Figura 1).

Figura 1: Rappresentazione grafica semplificata del paradosso di Simpson. Sulle ascisse e le ordinate sono rappresentati i possibili valori di due variabili quantitative. I dati, aggregati insieme, producono un andamento decrescente (linea tratteggiata). Osservandoli invece come gruppi diversi, l’andamento è invertito (linee colorate).
Il paradosso di Simpson si può incontrare in analisi di scienze sociali e ricerche mediche [4], il che non fa altro che sottolineare come davanti a un problema complesso non sia intellettualmente onesto accontentarsi di risposte semplici.
In generale, quindi, è bene ricordare che i dati “non parlano da soli” ma serve avere le competenze per poterli analizzare. A volte ci si può convincere, anche in buona fede, di conclusioni non corrette, perché si è data un’interpretazione che ignora alcune variabili del fenomeno.
Note
1) Simpson, E. H. (1951). The interpretation of interaction in contingency tables. Journal of the Royal Statistical Society: Series B (Methodological), 13(2), 238-241.
2) G. Travaglini, “Il paradosso di Simpson”, in Emmeciquadro n. 71, 2018, disponibile online qui: https://bit.ly/3wXZY0k
3) Pearl, Judea, Understanding Simpson's Paradox (September 19, 2013). Available at SSRN: https://bit.ly/3mWy2oX
4) Selvitella, A. (2017). The ubiquity of the Simpson’s Paradox. Journal of Statistical Distributions and Applications, 4(1), 1-16. Gruppo trattato con farmaco