Per aiutare gli studenti a prendere coscienza di quanto sia importante basarsi sui fatti (avvalorati da prove concrete) e non semplicemente sulle opinioni, abbiamo sviluppato un’indagine su alcune credenze molto diffuse nel nostro territorio; tali credenze sono state rintracciate in alcuni proverbi che riguardano il clima e le previsioni meteo e, grazie ad un’analisi dei dati climatici forniti dal Centro Funzionale di Aosta, si è voluta analizzarne la veridicità. Va premesso che i proverbi tradizionali sono fondati sulla buona capacità osservativa di coloro che, per esempio contadini o allevatori, hanno da sempre l’esigenza di prevedere quale sarà il tempo atmosferico nei giorni a seguire, per poter progettare attività quali semina, raccolto, taglio delle erbe da fieno ecc. Come ben sappiamo, però, anche una buona capacità di osservazione non garantisce di per sé circa il valore del risultato finale. Il punto quindi non è prendere le distanze da una cultura tradizionale, che va invece conosciuta e apprezzata nel suo divenire storico, ma invece quello di provare ad analizzare queste credenze, come esempi di ciò che diamo per scontato e che magari, ad un'indagine accurata, può rivelarsi sbagliato.
Tutti infatti conoscono proverbi come “rosso di sera bel tempo si spera” o “cielo a pecorelle, pioggia a catinelle”, ma può essere utile analizzarne l'adeguatezza per scoprire, magari, che proprio ciò che abbiamo sempre ritenuto perfettamente affidabile non lo era, e per imparare a riconoscere quanto spesso ci limitiamo a prendere per vero qualcosa solo perché ci viene raccontato da qualcuno di cui ci fidiamo.

I proverbi presi in esame
• Se è bello il giorno di S.Orso, l'orso si gira dall'altra parte (gira il pagliericcio) e fa ancora l'inverno per 40 giorni.
• Se piove a San Medardo, 40 giorni di cascate d'acqua.
• Il tempo del 1° di novembre è come quello di Natale.
• Natale al sole, Pasqua ai termosifoni.
• Se piove a San Dionigi, per tutto l'inverno ci sarà pioggia.
• Marzo arido (senza pioggia), aprile umido (piovoso).
• I giorni della merla sono i più freddi dell’anno.
• Santa Caterina porta sempre la neve.

Uno dei problemi principali nell’effettuare un'analisi approfondita di tali proverbi è l'interpretazione del testo: come considerare infatti frasi del tipo “cascate d’acqua” o “se è bello il giorno di...”? Questa terminologia è infatti molto soggettiva in quanto non fornisce valori di riferimento precisi. Il termine “bel tempo”, ad esempio, si presta infatti a diverse interpretazioni che dipendono dall’osservatore, dalla sua percezione sensoriale, dal suo vissuto. Nella sezione che presenta i dati analizzati, per ogni proverbio vengono indicate le soluzioni adottate nell’interpretazione del testo.
Per alcuni proverbi si è resa necessaria un’analisi anche tramite il Test statistico del chi-quadrato (χ2). Esso permette di confrontare una serie di dati osservati sperimentalmente con la serie dei dati attesi in base a un'ipotesi teorica e di stimare la bontà di questa ipotesi. Come soglia di significatività è stato preso il valore della probabilità dell’1%. Questo ci permette di dire che, nel caso in cui i valori osservati si discostino da quelli attesi, sarà da considerarsi significativa (non dovuta al caso) una situazione in cui il valore della probabilità restituito dal Test sia minore dell’1% (p<0,01).

Le stazioni meteorologiche utilizzate

Per il lavoro sono stati utilizzati i dati climatici registrati da 5 stazioni di rilevamento meteorologico tra quelle presenti sul territorio regionale: Aosta (Centrale idroelettrica); Brusson (Centrale idroelettrica); Gressoney-La-Trinité (loc. D'Ejola); Valgrisenche (diga Beauregard); Valtournenche (Lago Cignana).
Queste stazioni sono state scelte perché offrono una mole di dati statisticamente valida (minimo 30 anni) e, allo stesso tempo, coprono una buona porzione della Valle d’Aosta. I dati climatici forniti (in formato Excel) dal Centro Funzionale di Aosta hanno dato informazioni precise sulle precipitazioni giornaliere e sulla temperatura media giornaliera in un arco temporale tra il 1900 e il 2007 come mostra la tabella 1. Sono stati esclusi tutti gli anni per i quali non erano presenti dati climatici relativi ai periodi interessati dai vari proverbi.
A partire da questi dati grezzi si è potuto sviluppare un’analisi mirata alla verifica statistica dei proverbi elencati in precedenza permettendo in primo luogo agli studenti di imparare (in collaborazione con la Docente di Informatica) a utilizzare il foglio di calcolo Excel. Questo studio ha poi permesso ai ragazzi di avvicinarsi alle vecchie e nuove tecnologie a disposizione dei centri di elaborazione dei dati meteorologici che, oltre a permettere di conoscere la situazione climatica regionale del passato, consentono agli esperti di formulare le previsioni meteorologiche future.

Tabella 1
Giorno	Gressoney La Trinité - D'Ejola Precipitazione Giornaliera (mm) {Som}	Gressoney La Trinité - D'Ejola Termometro (°C)
01/03/1928	0	-2,6
02/03/1928	1,3	-0,8
03/03/1928	0,5	-0,5
04/03/1928	0	-0,9
05/03/1928	2,8	-0,1
06/03/1928	0	1,4
07/03/1928	0	1,1
08/03/1928	0	0,8
09/03/1928	0	0,2
10/03/1928	5	-0,1
11/03/1928	0,6	-0,3
12/03/1928	0	-2,1
13/03/1928	6,1	-1,3
14/03/1928	4,7	1,6
15/03/1928	0	-0,9
16/03/1928	0	-3,2
18/03/1928	0	-4,4
19/03/1928	0	-4,8
20/03/1928	1,9	-4,3
21/03/1928	5	-7,2
22/03/1928	2,8	-4,2
23/03/1928	10	-1,1
24/03/1928	4,3	0,9
25/03/1928	14,9	0,9
26/03/1928	19,2	-0,4
27/03/1928	0	2,3

Risultati

Se è bello il giorno di Sant’Orso,
l'orso si gira dall'altra parte (gira il pagliericcio)
e fa ancora l'inverno per 40 giorni.
È forse il proverbio più conosciuto in Valle d’Aosta ma è anche uno dei più difficili da analizzare in quanto presenta due affermazioni (Se è bello il giorno di S.Orso - fa ancora l'inverno per 40 giorni) difficilmente interpretabili in modo univoco. Cosa significano infatti “fa bello” e “fa ancora l’inverno”?
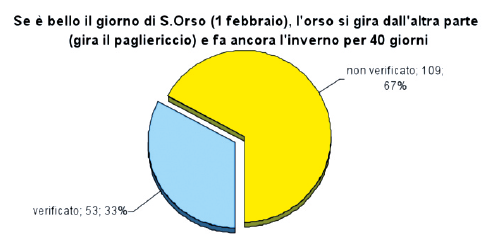
Per l'analisi si è considerata verificata la prima condizione in assenza di precipitazioni atmosferiche (precipitazioni = 0); la seconda condizione è stata considerata verificata nel caso di precipitazioni maggiori della media (dei 40 giorni) e temperatura media giornaliera minore della media (dei 40 giorni). Come si vede dal grafico1, i dati forniti dalle cinque stazioni meteo mostrano che il proverbio si è mostrato affidabile il 33% delle volte, mentre non si sono verificate le condizioni indicate sopra nel 67% delle volte.
È stata effettuata un’analisi dei dati, con il Test statistico del chi-quadrato, suddivisa in due parti, la prima parte riguardante la relazione tra le condizioni climatiche del giorno di Sant’Orso (1°febbraio) e le temperature registrate nei 40 giorni successivi, la seconda parte riguardante la relazione con le precipitazioni registrate sempre nel medesimo periodo. Per quanto riguarda le precipitazioni, il Test indica che la differenza tra i valori attesi e quelli osservati è dovuta al caso e quindi non esiste una relazione tra i due eventi.
Al contrario, per quanto riguarda le temperature, il valore elaborato dal Test è da considerarsi significativo ( p = 0,0034) ma a sfavore del proverbio; in altre parole, è più probabile che, se il giorno di Sant’Orso non si sono verificate precipitazioni atmosferiche, lo stesso accadrà nei 40 giorni seguenti.

Se piove a San Medardo, 40 giorni di cascate d'acqua

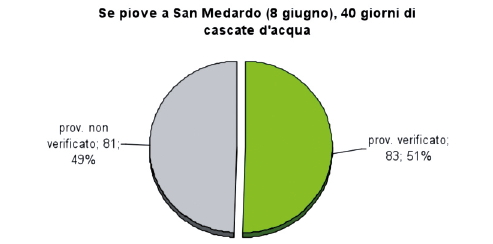
Il proverbio viene considerato verificato se il giorno di San Medardo (8 giugno) le precipitazioni sono maggiori di zero e, nei 40 giorni successivi, la sommatoria delle precipitazioni è maggiore della media dello stesso periodo (nella Tabella 2, colorati di verde, due anni nei quali si verificano le condizioni sopraccitate).

Tabella 2
San Medardo	prec. mm	sommatoria prec 40 gg succ.
08/06/1928	0	55,5
08/06/1929	0	98,6
08/06/1930	0	59
08/06/1931	0	78,7
08/06/1932	0,3	189,3
08/06/1933	2,8	155,3
08/06/1934	0,2	89,6
08/06/1935	0	71
08/06/1936	0	105,3

Nel Grafico 2 è possibile vedere che, per gli anni considerati validi delle 5 stazioni prese in considerazione, il proverbio è verificato nel 51% delle volte. L’analisi statistica con il test del chi-quadrato (v. tabella 3) restituisce un valore non significativo (p = 0,026).
Dobbiamo quindi ritenere valida l’ipotesi che le differenze tra i valori osservati e quelli attesi siano dovute al caso e che quindi non ci sia una correlazione tra le precipitazioni atmosferiche nel giorno di San Medardo e quelle dei 40 giorni successivi.

Tabella 3
	piove a SM	non piove a SM
piogg>media	83	98
piogg	81	150
VALORI OSSERVATI
	piove a SM	non piove a SM	Totale	Freq relativa
piogg>media	83	98	181	43,9%
piogg	81	150	231	56,1%
Totale	164	248	412	100%
Freq relativa	39,8%	60,2%	100%
FREQUENZE ATTESE
	piove a SM	non piove a SM	Totale
piogg>media	72,05	108,95	181
piogg	91,95	139,05	231
Totale	164	248
test chi-quadrato	0,0264

Il tempo del 1° di novembre è come quello di Natale

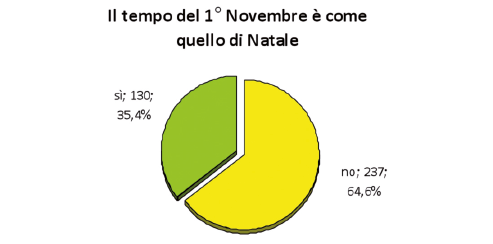
L’analisi dei dati climatici valdostani ci permette di affermare senza ombra di dubbio che è alquanto improbabile (per non dire impossibile) che il 1° novembre e il 25 dicembre si verifichino le stesse condizioni meteorologiche, a dicembre fa perlomeno molto più freddo. Per verificare allora l’attendibilità di questo proverbio si è ragionato nel seguente modo: si sono riportati in una tabella i valori di precipitazione e temperatura dei due giorni e il proverbio è stato considerato verificato nel caso in cui nei due giorni presi in esame si siano registrati andamenti simili (rispetto alla media) per quanto riguarda le precipitazioni e per quanto riguarda le temperature.

Le combinazioni che verificano il proverbio sono le seguenti:
• precipitazioni < media e temperature < media
• precipitazioni < media e temperature >media
• precipitazioni > media e temperature < media
• precipitazioni > media e temperature > media

La tabella 4 è una di quelle utilizzate; gli anni colorati in verde sono quelli che mostrano alcune delle condizioni riportate sopra.

Tabella 4
Anni	Prec. Gior. mm		Temp. media °C
	01-nov	25-dic	01-nov	25-dic
1931	0	0	1	-4
1932	9	0	-5	-4
1933	0	0	-3,5	-1,5
1934	5,2	0	-2,5	-7,5
1935	0	16	4	-3,5
1936	0	0	0	-0,5
1937	0,2	0	1,5	-0,5
1938	0	0	4,5	9,5
1939	0	0	2,5	-3,5
1940	0	0	7,5	-13
1941	0	0	-4,5	1
1942	37,8	4,7	1,5	-5
1943	0	0	3,5	-7
1944	0	0	-2,5	-13
1945	64	7	2,5	-7,5
1946	0	0	-4,5	-7
1947	12	0	0	4
1948	0	0	3,5	0,5
1949	0	0	1	0,5
1950	0	0	3	0,5
1951	10	0	-2	4

Le combinazioni che verificano il proverbio si verificano nel 35.4% dei casi mentre non si verificano nel 64.6%. (v. grafico 3)



Il Test del chi-quadrato per le temperature indica che non c’è relazione tra i due eventi; per quanto riguarda le precipitazioni, il Test restituisce un valore di poco non significativo (p = 0,021) il che non ci permette di confermare una correlazione statisticamente significativa tra il clima del 1° novembre e quello di Natale (v. Tabella 5).

Tabella 5
TEMPERATURE
Frequenze osservate	1 nov < media	1 nov. > media	Totale	Freq. marginale
25 dic. < media	90	94	184	50,14%
25 dic. > media	90	93	183	49,86%
Totale	180	187	367	100%
Freq. marginale	49%	51%	100%
Frequenze teoriche	1 nov. < media	1 nov. > media
25 dic. < media	90,25	93,75
25 dic. > media	89,75	93,25
Totale	180	187
Test chi-quadrato	0,9592
PRECIPITAZIONI
Frequenze osservate	1 nov < media	1 nov. > media	Totale	Freq. marginale
25 dic. < media	251	52	303	82,56%
25 dic. > media	45	19	64	17,44%
Totale	296	71	367	100%
Freq. marginale	80,7%	19,3%	100%
Frequenze teoriche	1 nov. < media	1 nov. > media
25 dic. < media	244,38	58,62
25 dic. > media	51,62	12,38
Totale	296	71
Test chi-quadrato	0,0212

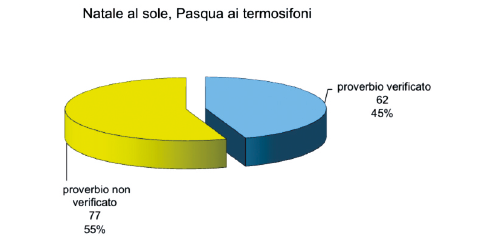
Natale al sole, Pasqua ai termosifoni

Questo proverbio viene interpretato dai valdostani nel modo seguente: se fa bello il giorno di Natale, allora a Pasqua farà freddo. Ritroviamo ancora una volta il problema dell’interpretazione di alcuni termini; si è stabilito che il proverbio è verificato quando si registrano tutte le seguenti condizioni:
• precipitazioni di Natale = 0 mm
• temperatura di Natale maggiore della media
• temperatura della Pasqua successiva minore della media


Il proverbio si verifica nel 45% dei casi presi in esame (v. Grafico 4) e il Test statistico del chi-quadrato (v. Tabella 6) ci restituisce un valore non significativo (p = 0,193); possiamo quindi affermare che le differenze tra i valori di precipitazione attesi e quelli osservati sono frutto del caso e non esiste una correlazione tra i due eventi esaminati.

Tabella 6
VALORI OSSERVATI
	Natale al sole	Natale alla pioggia	Totale	Freq relativa
Pasq t	62	94	156	48,8%
Pasq t>media	77	87	164	51,3%
Totale	139	181	320	100%
Freq relativa	43,4%	56,6%	100%
FREQUENZE ATTESE
	piove a SM	non piove a SM	Totale
piogg>media	67,76	88,24	156
piogg	71,24	92,76	164
Totale	139	181
test chi-quadrato	0,1935

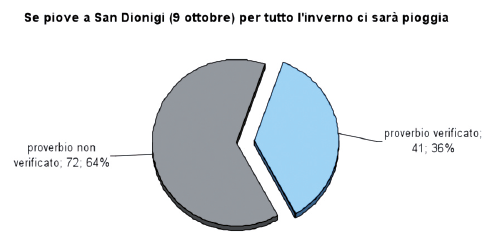
Se piove a San Dionigi, per tutto l'inverno ci sarà pioggia

Si sono presi in considerazione i dati pluviometrici del giorno di San Dionigi (9 ottobre) e si è verificato se, nel periodo invernale successivo, la sommatoria delle precipitazioni è stata superiore alla media del periodo. Nella tabella 7 sono colorati in blu gli anni in cui si registrano le condizioni sopraccitate. Queste si verificano nel 36% degli anni esaminati, come mostra l’areogramma riportato nel grafico 5:

Tabella 7
San Dionigi	prec. mm	prec. invernali mm
09/10/1920	4	34
09/10/1921	0	69
09/10/1922	0	86
09/10/1923	4	116
09/10/1924	0	100
09/10/1925	0	201
09/10/1926	12	112
09/10/1927	0	76
09/10/1929	6	161,5
09/10/1930	2,5	89
09/10/1931	0	73
09/10/1932	3,5	45
09/10/1933	0	137,5
09/10/1934	0	47,5
09/10/1935	3	290,5

Il Test statistico del chi-quadrato ci restituisce un valore non significativo (p = 0,22), quindi è possibile affermare che non esiste una correlazione tra gli eventi presi in esame e che le differenze tra i valori osservati e quelli attesi (riportati nella tabella 8) sono frutto del caso.

Tabella 8
	piove a SD	non piove a SD
piogg>media	41	122
piogg	72	162
VALORI OSSERVATI
	piove a SD	non piove a SD	Totale	Freq relativa
piogg>media	41	122	163	41,1%
piogg	72	162	234	58,9%
Totale	113	284	397	100%
Freq relativa	28,5%	71,5%	100%
FREQUENZE ATTESE
	piove a SM	non piove a SM	Totale
piogg>media	46,40	116,6	163
piogg	66,6	167,4	234
Totale	113	284
test chi-quadrato	0,2225

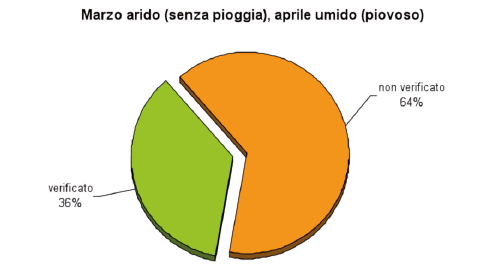
Marzo arido (senza pioggia), aprile umido (piovoso)

Si sono presi in considerazione i dati pluviometrici delle 5 stazioni per confrontare i dati relativi alla sommatoria delle piogge di marzo e di quelle di aprile. È praticamente impossibile trovare un mese di marzo senza pioggia (come recita il detto). Per ovviare al problema si sono calcolate le due medie (precipitazioni medie di marzo e precipitazioni medie di aprile); il proverbio è da considerarsi verificato se la precipitazione di marzo è minore della media e la precipitazione di aprile è maggiore della media. Tali condizioni si verificano nel 3grafico_6.png6% delle volte, come ci mostra il grafico 6.



Il Test del chi-quadrato (Tabella 9) ci fornisce un valore non significativo (p = 0,158), quindi non è possibile supporre l’esistenza di una correlazione tra le precipitazioni di marzo e quelle di aprile.

Tabella 9
	aprile piovoso	aprile arido
marzo arido	86	154
marzo piovoso	71	95
VALORI OSSERVATI
	aprile piovoso	aprile arido	Totale	Freq relativa
marzo arido	86	154	240	59,1%
marzo piovoso	71	95	166	40,9%
Totale	157	249	406	100%
Freq relativa	38,7%	61,3%	100%
FREQUENZE ATTESE
	piove a SM	non piove a SM	Totale
piogg>media	92,81	147,19	240
piogg	64,19	101,81	166
Totale	157	249
test chi-quadrato	0,1582

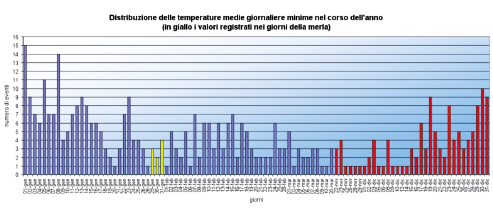
I giorni della merla sono i più freddi dell’anno

Questo è probabilmente uno dei proverbi più conosciuti in tutta Italia e viene associato alla leggenda secondo la quale per ripararsi dal gran freddo, una merla e i suoi pulcini, in origine bianchi, si rifugiarono dentro un comignolo, dal quale uscirono il 1º febbraio, tutti neri a causa della fuliggine.
Per verificare se davvero i giorni della merla (29, 30 e 31 gennaio) sono i più freddi dell’anno si sono elaborate delle tabelle che confrontano i valori delle temperature minime di tali giorni con i valori minimi dell’intero anno solare.
Nell’istogramma (Grafico 7) sono riportati sull’asse orizzontale i giorni dell’anno in cui si sono registrati i valori più bassi delle temperature e sull’asse verticale il numero di anni in cui si è verificata questa condizione; le colonne in blu comprendono il periodo dal 1°gennaio al 20 marzo, quelle in giallo rappresentano i 3 giorni della merla e le colonne rosse comprendono il periodo dal 22 novembre al 31 dicembre.



Come si può facilmente osservare, per quanto riguarda le 5 stazioni meteorologiche prese in considerazione, i giorni più freddi risultano essere quelli compresi tra l’ultima settimana di dicembre e i primi quindici giorni dell’anno, con un picco il 1° gennaio; non mancano altresì anni con picchi di freddo nell’intorno dei giorni della merla o addirittura nel mese di marzo. In sostanza, possiamo concludere che, senza nulla togliere al fascino della leggenda sull’origine del colore dei merli, i dati climatici presi in esame confutano il proverbio.

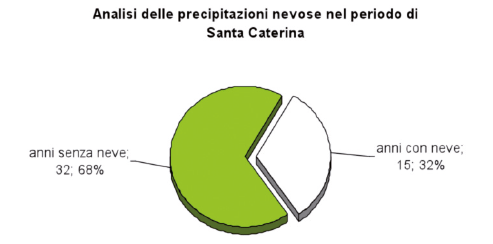
Santa Caterina porta sempre la neve

Secondo questo proverbio, il giorno di Santa Caterina (che cade il 25 novembre) sarebbe associato a precipitazioni nevose; considerato che il detto potrebbe non avere un rapporto di causa-effetto sicuro al 100% (parliamo comunque di previsioni e non di certezze) si è andati ad analizzare la situazione climatica reale considerando una “finestra” di 8 giorni intorno al 25 novembre (il giorno esatto, i due giorni precedenti e i cinque successivi), come indicato nella tabella 10.
Anche se, per questo proverbio, è stato possibile utilizzare un’unica stazione di rilevamento (quella di Aosta), i dati sono molto chiari. Nel grafico 8 sono riassunti i risultati ottenuti: dei 47 anni presi in esame, 32 (il 68% delle volte) non presentano nevicate, mentre 15 (il 32% del totale) confermano il proverbio.
La percentuale è nettamente a sfavore di ciò che viene comunemente affermato.

Tabella 10
Giorno	Aosta - Centrale idroelettrica Nivometro (cm)
22/11/1943	15
23/11/1943	10
24/11/1943	5
25/11/1943	23
26/11/1943	20
27/11/1943	18
28/11/1943	15
29/11/1943	12
30/11/1943	10
01/12/1943	8

Conclusioni

Spesso ci si dimentica che il meteorologo, non avendo a disposizione una sfera di cristallo funzionante, deve basare le sue previsioni su modelli matematici che forniscono appunto una previsione (non una certezza assoluta) delle condizioni atmosferiche future. Non possiamo quindi pretendere di sapere con precisione assoluta se, tra una settimana, pioverà o meno nel giardino di casa nostra. Se si riflette poi sul fatto che le indicazioni fornite sono il risultato di elaborazioni al computer di milioni di dati raccolti dalle varie stazioni di rilevamento sul territorio e da informazioni inviate dal satellite geostazionario, non è difficile comprendere quanto sia arduo prevedere gli eventi climatici; le variabili in gioco sono moltissime e gli errori di valutazione possono certo capitare. Ma se questa è la situazione di oggi, cosa si può dire allora delle previsioni (anche a lungo termine) del passato?
È davvero pensabile che, senza l’ausilio di tutte le tecnologie moderne, si potesse davvero prevedere un evento meteorologico con mesi di anticipo solo con la semplice osservazione (soggettiva) sul campo?
L’analisi dei dati climatici e la loro interpretazione statistica nel presente lavoro ci porterebbe a dare una risposta negativa. Certamente potrebbe essere interessante ampliare la ricerca anche ad altre zone d’Italia per una visione più completa della situazione. Sarebbe bello se esistessero davvero relazioni di causa-effetto come quelle descritte nei proverbi presi in esame, sicuramente gli addetti ai lavori avrebbero meno calcoli da fare e forse non si attirerebbero più le ire di molti gitanti. Troppo spesso, infatti, i meteorologi sono considerati i responsabili di un week-end rovinato dall’arrivo di un’improvvisa perturbazione temporalesca e incolpati dai vacanzieri del deplorevole “crimine” di non averlo previsto.

Ringraziamenti

Il progetto scolastico descritto in queste pagine non avrebbe visto la luce senza la collaborazione e l’impegno di molte persone, primi tra tutti gli studenti delle classi coinvolte, che non solo hanno dimostrato interesse verso gli argomenti trattati, ma hanno anche lavorato in équipe per le analisi effettuate. Si ringrazia caldamente il Dirigente Scolastico Dott. Francesco Fazari che ha sempre sostenuto e incentivato il lavoro di ricerca e ha concesso l’uso di spazi e materiali scolastici.
Un ringraziamento particolare va: al Sindaco di Nus Dott.ssa Elida Baravex e alla Signora Ivana Chamoix senza le quali il lavoro sulle nascite non avrebbe potuto aver luogo; al Dottor Marco Letey e al Dottor Fabio Brunier del Centro Funzionale di Aosta per aver fornito i dati climatici e per il loro intervento in classe; al Dottor Francesco Grassi (socio effettivo del Comitato) per la videoconferenza sui “cerchi nel grano”; al Dottor Luca Antonelli del CICAP Piemonte per l’aiuto fornito in campo statistico; a tutti i membri del Comitato che ci hanno incoraggiato e a tutti coloro che direttamente o indirettamente hanno contribuito al nostro risultato.
Desideriamo infine ringraziare con sentita riconoscenza il Dottor Silvano Fuso per averci concesso il suo prezioso tempo, senza oneri per l’Istituzione Scolastica, per la realizzazione della conferenza di fine anno.

Le classi coinvolte nel progetto

classe 2A - Prof.ssa Alessandra Ventrice
Barailler Cécile
Bencardino Nicholas
Borney Chiara
Brulard Veronica
Cerise Nicola
Cerise Sylvie
Comin Maicol
Docourtil Marcel
El Ouadi Fatima Zahara
Fantino Beatrice
Favre Valentina
Girodo Angelin Laila
Henriod Alessandro
Najari Hicham
Ortu Alessio
Pieiller Ellis
Serino Nicolò
classe 2B - Prof. Andrea Berti
Alessi Deborah
Borroz Mattia
Brancazi Matias
Cannatà Giacomo
De Luca Simone
Ducly Elvio
Ed-Daouche Walid
Ghabbar Hamza
Giarrusso Isabel
Giglio Matteo
Liquori Elisa
Macori Maurizio
Ottolenghi Ileana
Pianezzola Martina
Schiatti Mattia
Spataro Giuseppe
Turato Micol