Paradosso del baricentro
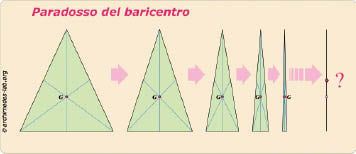
Supponiamo che la base di un triangolo isoscele venga divisa ripetutamente per N, facendo in modo però di mantenere l’altezza invariata. Se ne ricava che, a ogni iterazione, il baricentro del suddetto triangolo, trovandosi nel punto d’intersezione delle mediane, rimarrà nello stesso punto geometrico, cioè a un 1/3 dell’altezza dalla base (v. illustrazione).
Se portiamo quest’operazione al limite, il triangolo degenererà in una linea retta. Il fatto curioso è che questa ’riduzione’ finale sposterà ’magicamente’ il baricentro da 1/3 alla metà dell’altezza o, meglio, a metà della lunghezza del segmento (infatti, il centro di gravità di una retta coincide con il suo punto medio!). Come ciò è possibile?
Dov’è l’errore?
Il triangolo è un oggetto geometrico bidimensionale, mentre una retta è monodimensionale. Di conseguenza, rispondono a leggi diverse. Le trasformazioni successive del triangolo tendono indubbiamente verso un limite: il famoso segmento. Però, la natura del triangolo rimarrà tale anche dopo molte riduzioni della base e il suo perimetro non potrà mai coincidere con la lunghezza di un segmento.
Potete discutere dell’argomento sul nostro sito web:
http://goo.gl/v6W3J