L'illusione della Luna consiste nel fatto che la Luna, il Sole e le costellazioni sembrano — ma non sono — molto più grandi quando sono vicini all’orizzonte rispetto a quando sono alti nel cielo.
Nell’articolo precedente di questa rubrica (v. Query 20) ho descritto i fattori che influenzano il fenomeno, concludendo che i principali sono la visibilità del terreno e la distanza apparente dell’orizzonte: l’illusione è tanto più forte quanto più l’orizzonte sembra lontano e quanto più visibile è il terreno che intercorre tra esso e l’osservatore.
Qui e nel prossimo articolo descriverò invece le due principali spiegazioni dell’illusione che sono attualmente in competizione tra loro, ma si tenga presente che nel corso dei secoli ne sono state proposte tante altre.
Secondo la prima di tali spiegazioni — che quasi tutti gli scritti divulgativi sull’argomento presentano, sbagliando, come se fosse universalmente accettata — la grandezza fenomenica (cioè apparente, percepita) della Luna è funzione della sua distanza fenomenica: quando è vicina all’orizzonte, la Luna sembra più grande perché sembra più lontana rispetto a quando è alta nel cielo. A prima vista, ciò può apparire in contrasto con la comune esperienza secondo cui un oggetto sembra tanto più piccolo, non tanto più grande, quanto più è distante.
Però, un oggetto sembra rimpicciolirsi quando si allontana da noi perché diminuisce la sua grandezza angolare (che può essere molto informalmente definita come la porzione di campo visivo occupata dall’oggetto); ma la Luna ha sempre la stessa grandezza angolare a qualsiasi distanza sembri trovarsi, e quando due oggetti che hanno le stesse dimensioni angolari sembrano a distanze diverse, come la Luna all’orizzonte e quella allo zenit, quello dei due che sembra più lontano sembra anche più grande. Ciò è dovuto alla cosiddetta costanza di grandezza, ossia alla tendenza degli oggetti a conservare più o meno le proprie dimensioni fenomeniche al variare — entro certi limiti — della loro distanza da noi e quindi della loro grandezza angolare.
Ad esempio, una persona ci sembra solo un po' più piccola quando è a 10 metri di distanza rispetto a quando è a 5 metri; ma se la grandezza fenomenica fosse funzione esclusivamente della grandezza angolare, essa dovrebbe sembrarci molto più piccola di così, e cioè esattamente la metà.
Se ciò non avviene è perché, in qualche modo ancora in buona parte ignoto, il nostro cervello “calcola” la grandezza fenomenica di un oggetto tenendo conto della distanza di quell’oggetto dall’osservatore (si tenga però presente che non tutti sono d’accordo su questo punto).
Semplificando in modo un po’ scandaloso, la relazione tra grandezza angolare, grandezza fenomenica e distanza fenomenica è più o meno la seguente:
“grandezza fenomenica”
=
“grandezza angolare”
x
“distanza fenomenica”
Questa equazione implica, tra le altre cose, che quando due oggetti hanno la stessa grandezza angolare, quello dei due che sembra più lontano sembri anche più grande; quindi, se la Luna sembra più lontana quando è all'orizzonte, essa deve sembrare — e infatti sembra —più grande in tale posizione.
È semplice sperimentare di persona la costanza di grandezza, ad esempio nel modo seguente. Si fissi per circa 40 secondi la croce di sinistra della Figura 1, spostando poi lo sguardo sulla croce di destra: si vedrà un disco illusorio più o meno azzurro (si tratta di un’immagine consecutiva negativa). Si allontani poi la pagina da sé, continuando a fissare la croce di destra: si noterà che il disco illusorio si espanderà tanto più quanto più si allontanerà la pagina. Se poi si sposterà lo sguardo su una parete distante un paio di metri, l'espansione sarà ancora maggiore.
Ecco come viene in genere spiegato questo fenomeno. Quando si allontana la pagina, anche l'immagine consecutiva sembra allontanarsi, perché continua a essere vista sulla pagina; poiché sembra più lontana, e poiché le sue dimensioni angolari rimangono costanti, la sua grandezza fenomenica aumenta.
Secondo chi accetta la spiegazione basata sulla costanza di grandezza, la luna si comporta proprio come le immagini consecutive, e infatti uno dei metodi utilizzati nello studio dell’illusione della Luna è basato appunto su queste ultime: dopo aver generato un'immagine consecutiva si fissano varie posizioni nel cielo, constatando che il disco illusorio raggiunge la sua massima grandezza apparente quando lo si "proietta" appena sopra l'orizzonte. È un metodo impreciso ma utile per chi voglia sperimentare in proprio.
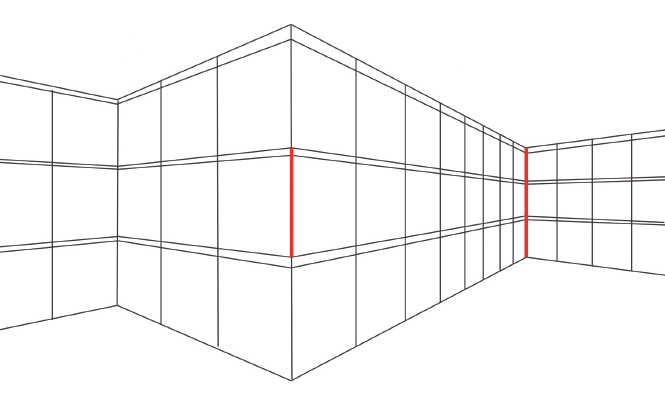
Nella vita quotidiana la costanza di grandezza, come le altre costanze (di forma, di colore, etc), ci aiuta a percepire il mondo correttamente, ma talvolta il cervello la applica anche quando ciò non è appropriato, il che genera parecchie altre illusioni, oltre (forse) a quella della Luna. Ad esempio, è probabile che si spieghi così la versione della nota illusione di Müller-Lyer illustrata nella figura 2 (e adattata da I. Rock, Perception, New York: Scientific American Library, 1984). Le due linee rosse sono identiche, ma si stenta a crederlo: la linea di destra, infatti, sembra molto più lunga, ed è probabile che sembri più lunga perché sembra più distante. L’illusione dei binari, di cui si mostra una versione nella fig. 3, può essere spiegata allo stesso modo. I due bastoni sono identici, ma quello che sembra più lontano sembra anche più grande.
Questa spiegazione dell'illusione della Luna risale almeno al X secolo, quando fu avanzata dall'importante scienziato arabo Ibn al-Haytham (Alhazen), ed è stata avallata, nel corso dei secoli, da moltissimi studiosi. Nella versione di Robert Smith (1738), essa prevede che la distanza a cui percepiamo la Luna sia determinata dalla forma apparente del cielo. Già si è detto in un precedente articolo sull’illusione dell’elevazione (Query n° 19) che secondo Smith il cielo ha l’aspetto di una volta ribassata al centro.
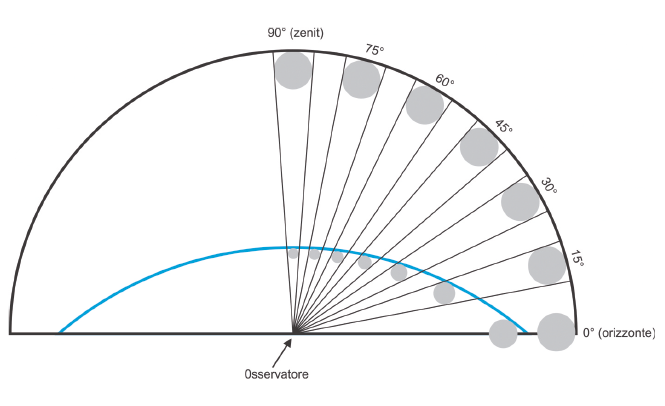
Nella figura 4, l'arco azzurro rappresenta la volta del cielo, ribassata al centro, su cui secondo Smith sembra collocata la Luna: come si può vedere, se Smith ha ragione la Luna deve sembrare sempre più grande man mano che si avvicina all’orizzonte, perché sembra allontanarsi sempre più dall'osservatore mantenendo le stesse dimensioni angolari.
La spiegazione di Smith è però accettata oggi, al massimo, come spiegazione parziale. Si ricorderà, infatti, che i fattori più importanti tra quelli che determinano l’illusione sono la visibilità del terreno e la distanza apparente dell’orizzonte, fattori con cui la forma del cielo sembra aver poco a che vedere.
Secondo chi accetta la spiegazione basata sulla costanza di grandezza, il terreno è importante perché contribuisce ad allontanare l’orizzonte. Una delle ragioni per cui si suppone che esso abbia questo effetto è che gli spazi disomogenei sembrano più ampi di quelli omogenei, come si è detto e dimostrato nell’articolo precedente; ma il terreno che intercorre tra noi e l’orizzonte è appunto molto disomogeneo, perché contiene oggetti e tessiture di ogni sorta, e sembra quindi maggiore dello spazio in genere omogeneo che intercorre tra noi e la Luna alta nel cielo.
Le spiegazioni basate sulla costanza di grandezza sono a prima vista molto persuasive, ma si imbattono in una difficoltà che alcuni ritengono decisiva. Potrà sembrare incredibile, perché si direbbe che basti guardare per capire come stanno le cose, ma pare proprio che non sia vero che la Luna sembra più lontana quando è vicina all'orizzonte, come si è affermato per almeno un millennio!
La maggior parte delle persone, infatti, se le si interroga in proposito, come si è cominciato a fare solo alla fine dell’Ottocento, dice proprio l’opposto, e cioè che quando è vicina all’orizzonte la Luna sembra più vicina o al massimo alla stessa distanza di quando è alta nel cielo!
Comprensibilmente, questo fatto è stato ed è la principale ragione per cui si sono cercate spiegazioni alternative a quella basata sulla costanza di grandezza.
Nel prossimo articolo parlerò della più importante tra queste spiegazioni alternative.
Nell’articolo precedente di questa rubrica (v. Query 20) ho descritto i fattori che influenzano il fenomeno, concludendo che i principali sono la visibilità del terreno e la distanza apparente dell’orizzonte: l’illusione è tanto più forte quanto più l’orizzonte sembra lontano e quanto più visibile è il terreno che intercorre tra esso e l’osservatore.
Qui e nel prossimo articolo descriverò invece le due principali spiegazioni dell’illusione che sono attualmente in competizione tra loro, ma si tenga presente che nel corso dei secoli ne sono state proposte tante altre.
Secondo la prima di tali spiegazioni — che quasi tutti gli scritti divulgativi sull’argomento presentano, sbagliando, come se fosse universalmente accettata — la grandezza fenomenica (cioè apparente, percepita) della Luna è funzione della sua distanza fenomenica: quando è vicina all’orizzonte, la Luna sembra più grande perché sembra più lontana rispetto a quando è alta nel cielo. A prima vista, ciò può apparire in contrasto con la comune esperienza secondo cui un oggetto sembra tanto più piccolo, non tanto più grande, quanto più è distante.
Però, un oggetto sembra rimpicciolirsi quando si allontana da noi perché diminuisce la sua grandezza angolare (che può essere molto informalmente definita come la porzione di campo visivo occupata dall’oggetto); ma la Luna ha sempre la stessa grandezza angolare a qualsiasi distanza sembri trovarsi, e quando due oggetti che hanno le stesse dimensioni angolari sembrano a distanze diverse, come la Luna all’orizzonte e quella allo zenit, quello dei due che sembra più lontano sembra anche più grande. Ciò è dovuto alla cosiddetta costanza di grandezza, ossia alla tendenza degli oggetti a conservare più o meno le proprie dimensioni fenomeniche al variare — entro certi limiti — della loro distanza da noi e quindi della loro grandezza angolare.
Ad esempio, una persona ci sembra solo un po' più piccola quando è a 10 metri di distanza rispetto a quando è a 5 metri; ma se la grandezza fenomenica fosse funzione esclusivamente della grandezza angolare, essa dovrebbe sembrarci molto più piccola di così, e cioè esattamente la metà.
Se ciò non avviene è perché, in qualche modo ancora in buona parte ignoto, il nostro cervello “calcola” la grandezza fenomenica di un oggetto tenendo conto della distanza di quell’oggetto dall’osservatore (si tenga però presente che non tutti sono d’accordo su questo punto).
Semplificando in modo un po’ scandaloso, la relazione tra grandezza angolare, grandezza fenomenica e distanza fenomenica è più o meno la seguente:
Questa equazione implica, tra le altre cose, che quando due oggetti hanno la stessa grandezza angolare, quello dei due che sembra più lontano sembri anche più grande; quindi, se la Luna sembra più lontana quando è all'orizzonte, essa deve sembrare — e infatti sembra —più grande in tale posizione.
Figura 1.
Ecco come viene in genere spiegato questo fenomeno. Quando si allontana la pagina, anche l'immagine consecutiva sembra allontanarsi, perché continua a essere vista sulla pagina; poiché sembra più lontana, e poiché le sue dimensioni angolari rimangono costanti, la sua grandezza fenomenica aumenta.
Secondo chi accetta la spiegazione basata sulla costanza di grandezza, la luna si comporta proprio come le immagini consecutive, e infatti uno dei metodi utilizzati nello studio dell’illusione della Luna è basato appunto su queste ultime: dopo aver generato un'immagine consecutiva si fissano varie posizioni nel cielo, constatando che il disco illusorio raggiunge la sua massima grandezza apparente quando lo si "proietta" appena sopra l'orizzonte. È un metodo impreciso ma utile per chi voglia sperimentare in proprio.
Figura 2.
Figura 3.
Nella figura 4, l'arco azzurro rappresenta la volta del cielo, ribassata al centro, su cui secondo Smith sembra collocata la Luna: come si può vedere, se Smith ha ragione la Luna deve sembrare sempre più grande man mano che si avvicina all’orizzonte, perché sembra allontanarsi sempre più dall'osservatore mantenendo le stesse dimensioni angolari.
Figura 4.
Secondo chi accetta la spiegazione basata sulla costanza di grandezza, il terreno è importante perché contribuisce ad allontanare l’orizzonte. Una delle ragioni per cui si suppone che esso abbia questo effetto è che gli spazi disomogenei sembrano più ampi di quelli omogenei, come si è detto e dimostrato nell’articolo precedente; ma il terreno che intercorre tra noi e l’orizzonte è appunto molto disomogeneo, perché contiene oggetti e tessiture di ogni sorta, e sembra quindi maggiore dello spazio in genere omogeneo che intercorre tra noi e la Luna alta nel cielo.
Le spiegazioni basate sulla costanza di grandezza sono a prima vista molto persuasive, ma si imbattono in una difficoltà che alcuni ritengono decisiva. Potrà sembrare incredibile, perché si direbbe che basti guardare per capire come stanno le cose, ma pare proprio che non sia vero che la Luna sembra più lontana quando è vicina all'orizzonte, come si è affermato per almeno un millennio!
La maggior parte delle persone, infatti, se le si interroga in proposito, come si è cominciato a fare solo alla fine dell’Ottocento, dice proprio l’opposto, e cioè che quando è vicina all’orizzonte la Luna sembra più vicina o al massimo alla stessa distanza di quando è alta nel cielo!
Comprensibilmente, questo fatto è stato ed è la principale ragione per cui si sono cercate spiegazioni alternative a quella basata sulla costanza di grandezza.
Nel prossimo articolo parlerò della più importante tra queste spiegazioni alternative.
