Aristotele pensava che il cielo fosse una superficie solida perfettamente sferica sulla quale erano incastonate le stelle. Lo pensava non tanto perché gli sembrava, guardandolo, che esso avesse tale forma quanto perché tutti i dati osservativi sembravano dimostrare che esso non poteva che avere proprio quella forma. Solo per fare un esempio, il fatto che le stelle si muovono lungo archi di cerchio può essere spiegato in modo semplice solo assumendo che il cielo è sferico. Fu solo nel Seicento che si arrivò a capire che il cielo non ha in realtà nessuna forma, essendo sostanzialmente un’illusione. Ciò non toglie però che esso sembri avere una forma.
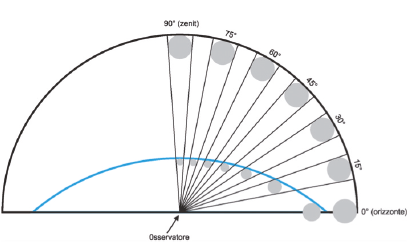
Il problema della forma apparente del cielo fu aggredito sperimentalmente per la prima volta solo nel 1738, dal matematico Robert Smith, il cui scopo era di spiegare l’illusione della Luna. Tra le molte illusioni osservabili in cielo quella della Luna è la più studiata in assoluto, e lo è da oltre due millenni. Essa consiste nel fatto che la Luna sembra molto più grande quando è vicina all'orizzonte rispetto a quando è alta nel cielo, mentre in realtà le sue dimensioni sono sempre le stesse (il fenomeno interessa anche il Sole e le costellazioni). Secondo Smith la causa dell’illusione sta nel fatto che il cielo sembra avere la forma di una volta ribassata al centro: il cielo che si vede all’orizzonte sembra, infatti, tre o quattro volte più lontano del cielo allo zenit (lo zenit è il punto del cielo proprio sopra la nostra testa).
Come si vede nella figura 1, che è molto simile a quella con cui Smith stesso illustra la propria spiegazione, e come chiarirò molto meglio in un prossimo articolo, se il cielo fosse percepito come una cupola ribassata al centro, la Luna, che sul cielo (l’arco azzurro) appare collocata, dovrebbe sembrare sempre più piccola man mano che si avvicina allo zenit, perché sembrerebbe avvicinarsi sempre più all'osservatore conservando al tempo stesso la propria grandezza angolare. Dal momento che ciò è appunto quanto si vede, Smith pensò di avere spiegato l’illusione della Luna.
Smith dimostrò che si verifica anche un altro fenomeno visivo, mai descritto prima di lui, che non può non aver luogo se il cielo ha davvero la forma che Smith gli attribuisce. Si tratta di un’illusione veramente clamorosa a cui però non è mai stato dato un nome; la chiamerò qui illusione dell’elevazione.
Essa consiste nel fatto che l'elevazione apparente dei corpi celesti (cioè la loro distanza apparente dall’orizzonte) è, per la maggior parte degli osservatori, molto superiore a quella reale. Smith consigliava questo metodo per rendersene conto: si individui un astro che abbia un’elevazione apparente di 45°, che cioè sembri esattamente a metà strada tra l’orizzonte e lo zenit; confrontando poi l’elevazione apparente dell’astro con quella reale si constaterà che quest’ultima è, mediamente, di circa 23°, cioè più vicina all’orizzonte di oltre 20° rispetto a quella apparente. (Si può accertare l’elevazione reale di un qualsiasi corpo celeste con Stellarium (http://www.stellarium.org/ ), un programma gratuito di astronomia.) È facile convincersi di persona, seguendo le istruzioni di Smith, che l’illusione non solo c’è ma è fortissima, soprattutto di giorno. Ad esempio, quando la Luna è a 45°, sembra veramente impossibile che essa si trovi solo a metà strada tra l’orizzonte e lo zenit: essa sembra davvero molto spostata verso lo zenit. Si può inoltre constatare facilmente di persona che l’illusione dell’elevazione non richiede che l’orizzonte sia visibile. Come suggerisce l’astronomo M. Minnaert (1993), di notte guardate sopra di voi e individuate una stella che vi sembra proprio allo zenit. Fate poi un mezzo giro su voi stessi e tornate a guardare la stessa stella: ora essa vi sembrerà molto distante dallo zenit, il che implica che la sua elevazione reale è distante dai 90° apparenti.
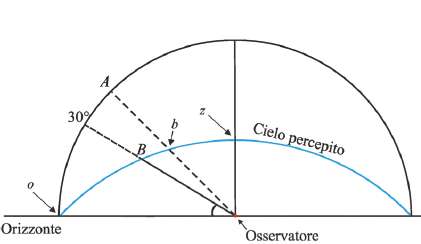
Nella figura 2 si mostra perché l’illusione dell’elevazione deve necessariamente aver luogo se è vero che la forma apparente del cielo è quella di una volta appiattita. Se percepissimo il cielo come una sfera con noi al centro, un qualsiasi astro ci sembrerebbe a metà strada tra l’orizzonte e lo zenit, correttamente, quando lo vediamo nella posizione A, cioè a 45°; se invece percepissimo il cielo come una volta ribassata, come sostiene Smith, l’astro dovrebbe sembrarci a metà strada tra l’orizzonte e lo zenit quando si trova a metà strada lungo l'arco oz (che è il cielo percepito), cioè quando si trova nella posizione B. Il fenomeno che si osserva è il secondo: l'astro ci sembra a metà strada quando è in B, mentre ci sembra decisamente spostato verso lo zenit quando è a 45° perché lo è realmente lungo l'arco oz, dal momento che noi lo percepiamo nella posizione b. Questa è indubbiamente una prova importante a supporto della tesi di Smith.
Le non poche indagini successive hanno sostanzialmente confermato la stima di Smith: ci sono differenze sensibili tra gli osservatori ma, mediamente, un astro sembra a 45° quando la sua elevazione reale è tra i 20° e i 30° (e talora di più). Si è trovato anche che l’illusione è più forte proprio in quelle condizioni in cui il cielo più somiglia a una volta appiattita. Essa è tanto più pronunciata, infatti, quanto più l’orizzonte sembra lontano, ed è più marcata quando il tempo è nuvoloso rispetto a quando è sereno. Kaufman e Rock (1989) riassumono nella Tabella 1 i valori ottenuti in alcune di queste ricerche.
TABELLA 1
Si sono studiate anche elevazioni diverse da 45°. Ad esempio, Schmeidler (2009) riporta i valori riassunti nella Tabella 2, anche se non precisa in quali condizioni essi sono stati ottenuti.
TABELLA 2
Secondo Smith diversi altri fenomeni sono spiegabili col fatto che il cielo ha la forma che lui gli attribuisce. Uno di questi fenomeni è stato descritto anche da Newton: la Luna non sembra al centro dell’alone che a volte la circonda, com’è in realtà, bensì decisamente più in alto. Un altro dei fenomeni che Smith spiega con la forma del cielo riguarda gli arcobaleni: le bande colorate che compongono un arcobaleno sembrano più ampie nella parte bassa dell'arcobaleno che in quella alta, mentre in realtà esse hanno un'ampiezza costante.
La tesi di Smith si diffuse rapidamente diventando quasi un dogma, e almeno fino all’inizio del secolo scorso si è dato in genere per scontato che il cielo abbia la forma suggerita da Smith. Ad esempio, per il nostro Giovanni Schiaparelli (1903), ricordato oggi soprattutto per aver descritto i famosi canali di Marte, la forma apparente del firmamento «come ognun vede, non è proprio una mezza sfera, ma piuttosto la metà di uno sferoide assai più esteso in direzione orizzontale». Schiaparelli nota anche che già Empedocle (unica eccezione tra gli antichi) «appoggiato alla testimonianza quotidiana dell’occhio, dichiarò il cielo non doversi ritenere come sferico, ma essere anzi la sua superficie schiacciata in senso verticale.» E secondo l’astronomo R. A. Proctor (1892) «l’impressione naturale dell’osservatore» è che il cielo abbia «una forma piuttosto appiattita, con l’orizzonte che sembra tra le tre e le quattro volte più distante» del cielo allo zenit.
Poi, però, qualcuno cominciò a sostenere che le cose non stanno proprio così, o almeno non sempre. Nessuno ha mai messo in dubbio che il cielo ha più o meno la forma di una calotta schiacciata quando il tempo è nuvoloso, perché le nubi all'orizzonte non solo sembrano ma sono realmente più distanti di quelle sopra di noi, ma alcuni hanno sostenuto, a mio parere con qualche ragione, che la forma del cielo è meno chiara quando il tempo è sereno. Soprattutto, in tanti hanno notato che il cielo sembra non avere proprio nessuna forma di notte. Ma l'illusione dell'elevazione è osservabile nell’intero arco delle 24 ore, per cui la spiegazione di Smith richiede che il cielo appaia schiacciato al centro anche di notte. Sulla questione, comunque, non è stato ancora emesso un verdetto definitivo, come spiegherò meglio nel prossimo articolo di questa rubrica, il cui oggetto sarà l’illusione della Luna.
Il problema della forma apparente del cielo fu aggredito sperimentalmente per la prima volta solo nel 1738, dal matematico Robert Smith, il cui scopo era di spiegare l’illusione della Luna. Tra le molte illusioni osservabili in cielo quella della Luna è la più studiata in assoluto, e lo è da oltre due millenni. Essa consiste nel fatto che la Luna sembra molto più grande quando è vicina all'orizzonte rispetto a quando è alta nel cielo, mentre in realtà le sue dimensioni sono sempre le stesse (il fenomeno interessa anche il Sole e le costellazioni). Secondo Smith la causa dell’illusione sta nel fatto che il cielo sembra avere la forma di una volta ribassata al centro: il cielo che si vede all’orizzonte sembra, infatti, tre o quattro volte più lontano del cielo allo zenit (lo zenit è il punto del cielo proprio sopra la nostra testa).
Figura 1
Smith dimostrò che si verifica anche un altro fenomeno visivo, mai descritto prima di lui, che non può non aver luogo se il cielo ha davvero la forma che Smith gli attribuisce. Si tratta di un’illusione veramente clamorosa a cui però non è mai stato dato un nome; la chiamerò qui illusione dell’elevazione.
Essa consiste nel fatto che l'elevazione apparente dei corpi celesti (cioè la loro distanza apparente dall’orizzonte) è, per la maggior parte degli osservatori, molto superiore a quella reale. Smith consigliava questo metodo per rendersene conto: si individui un astro che abbia un’elevazione apparente di 45°, che cioè sembri esattamente a metà strada tra l’orizzonte e lo zenit; confrontando poi l’elevazione apparente dell’astro con quella reale si constaterà che quest’ultima è, mediamente, di circa 23°, cioè più vicina all’orizzonte di oltre 20° rispetto a quella apparente. (Si può accertare l’elevazione reale di un qualsiasi corpo celeste con Stellarium (http://www.stellarium.org/ ), un programma gratuito di astronomia.) È facile convincersi di persona, seguendo le istruzioni di Smith, che l’illusione non solo c’è ma è fortissima, soprattutto di giorno. Ad esempio, quando la Luna è a 45°, sembra veramente impossibile che essa si trovi solo a metà strada tra l’orizzonte e lo zenit: essa sembra davvero molto spostata verso lo zenit. Si può inoltre constatare facilmente di persona che l’illusione dell’elevazione non richiede che l’orizzonte sia visibile. Come suggerisce l’astronomo M. Minnaert (1993), di notte guardate sopra di voi e individuate una stella che vi sembra proprio allo zenit. Fate poi un mezzo giro su voi stessi e tornate a guardare la stessa stella: ora essa vi sembrerà molto distante dallo zenit, il che implica che la sua elevazione reale è distante dai 90° apparenti.
Figura 2
Le non poche indagini successive hanno sostanzialmente confermato la stima di Smith: ci sono differenze sensibili tra gli osservatori ma, mediamente, un astro sembra a 45° quando la sua elevazione reale è tra i 20° e i 30° (e talora di più). Si è trovato anche che l’illusione è più forte proprio in quelle condizioni in cui il cielo più somiglia a una volta appiattita. Essa è tanto più pronunciata, infatti, quanto più l’orizzonte sembra lontano, ed è più marcata quando il tempo è nuvoloso rispetto a quando è sereno. Kaufman e Rock (1989) riassumono nella Tabella 1 i valori ottenuti in alcune di queste ricerche.
TABELLA 1
| Sereno | Nuvoloso | |
| Reimann (1902) | 20,6° | 22,5° |
| Dember e Uibe (1920) | 29° | 32° |
| Miller (1943) | 29,9° | 34° |
| Baird e Wagner (1982) | 37° | 42° |
Si sono studiate anche elevazioni diverse da 45°. Ad esempio, Schmeidler (2009) riporta i valori riassunti nella Tabella 2, anche se non precisa in quali condizioni essi sono stati ottenuti.
TABELLA 2
| ELEVAZIONE | ||
| Reale | Stimata | Illusione |
| 0° | 0° | 0° |
| 15° | 30° | 15° |
| 30° | 50° | 20° |
| 45° | 65° | 20° |
| 60° | 75° | 15° |
| 75° | 84° | 9° |
| 90° | 90° | 0° |
Secondo Smith diversi altri fenomeni sono spiegabili col fatto che il cielo ha la forma che lui gli attribuisce. Uno di questi fenomeni è stato descritto anche da Newton: la Luna non sembra al centro dell’alone che a volte la circonda, com’è in realtà, bensì decisamente più in alto. Un altro dei fenomeni che Smith spiega con la forma del cielo riguarda gli arcobaleni: le bande colorate che compongono un arcobaleno sembrano più ampie nella parte bassa dell'arcobaleno che in quella alta, mentre in realtà esse hanno un'ampiezza costante.
La tesi di Smith si diffuse rapidamente diventando quasi un dogma, e almeno fino all’inizio del secolo scorso si è dato in genere per scontato che il cielo abbia la forma suggerita da Smith. Ad esempio, per il nostro Giovanni Schiaparelli (1903), ricordato oggi soprattutto per aver descritto i famosi canali di Marte, la forma apparente del firmamento «come ognun vede, non è proprio una mezza sfera, ma piuttosto la metà di uno sferoide assai più esteso in direzione orizzontale». Schiaparelli nota anche che già Empedocle (unica eccezione tra gli antichi) «appoggiato alla testimonianza quotidiana dell’occhio, dichiarò il cielo non doversi ritenere come sferico, ma essere anzi la sua superficie schiacciata in senso verticale.» E secondo l’astronomo R. A. Proctor (1892) «l’impressione naturale dell’osservatore» è che il cielo abbia «una forma piuttosto appiattita, con l’orizzonte che sembra tra le tre e le quattro volte più distante» del cielo allo zenit.
Poi, però, qualcuno cominciò a sostenere che le cose non stanno proprio così, o almeno non sempre. Nessuno ha mai messo in dubbio che il cielo ha più o meno la forma di una calotta schiacciata quando il tempo è nuvoloso, perché le nubi all'orizzonte non solo sembrano ma sono realmente più distanti di quelle sopra di noi, ma alcuni hanno sostenuto, a mio parere con qualche ragione, che la forma del cielo è meno chiara quando il tempo è sereno. Soprattutto, in tanti hanno notato che il cielo sembra non avere proprio nessuna forma di notte. Ma l'illusione dell'elevazione è osservabile nell’intero arco delle 24 ore, per cui la spiegazione di Smith richiede che il cielo appaia schiacciato al centro anche di notte. Sulla questione, comunque, non è stato ancora emesso un verdetto definitivo, come spiegherò meglio nel prossimo articolo di questa rubrica, il cui oggetto sarà l’illusione della Luna.
Bibliografia
- Kaufman, L. & Rock, I. (1989). The moon illusion thirty years later. In: M. Hershenson (a cura di), The Moon Illusion, Hillsdale: Erlbaum, pagg. 193–234
- Minnaert, M. G. J. (1993). Light and Color in the Outdoors. Berlino: Springer-Verlag
- Proctor, R. A., & Ranyard, A. C. (1895). Old and New Astronomy. Londra: Longmans, Green, and Co.
- Schiaparelli, G. V. (1903). L'astronomia nell'Antico Testamento. Milano: Hoepli
- Schmeidler, F. (2009). The Terrestrial Atmosphere and Its Effects on Astronomical Observations. In: G. D. Roth (a cura di), Handbook of practical Astronomy, Berlino: Springer, pagg. 552-571
- Smith R. (1738). A compleat System of Opticks in Four Books. Cambridge
