Come scrive lo storico dell’astronomia Michael Hoskin (2001), «la storia della cosmologia non è la storia facile del rifiuto di idee assurde a favore di idee ... chiaramente vere, ma la saga eroica del rifiuto di ciò che sembra chiaramente vero a favore di ciò che sembra assurdo.» In effetti, per avvicinarsi alla verità gli astronomi dell’antichità dovettero combattere contro l’evidenza percettiva. Ciò vale anche per idee che oggi ci sembrano talmente scontate da non riuscire a capire come la si potrebbe pensare diversamente.
Si pensi ad esempio alle fasi lunari. Si riuscì a spiegarle, naturalmente, solo quando si arrivò a capire che la Luna splende perché è illuminata dal Sole. Pare che il primo a comprenderlo sia stato Anassagora (vissuto circa dal 510 al 428 a.C.), ma chi venne prima di lui credeva che la Luna brillasse di luce propria[1]. In effetti, le ragioni per pensare che la Luna rifletta la luce solare non sono molte[2], anche perché la vediamo splendere anche di notte, quando in cielo il Sole non c’è. La percezione visiva non suggerisce la risposta giusta; anzi, è legittimo il sospetto che essa abbia ritardato la scoperta della verità. Infatti, c’è almeno un fenomeno, che non ho trovato discusso nella letteratura a me nota sulla storia dell’astronomia, che sembra dimostrare in modo apparentemente incontrovertibile che la Luna non è illuminata dal Sole. Chiamerò tale fenomeno “illusione del terminatore”.
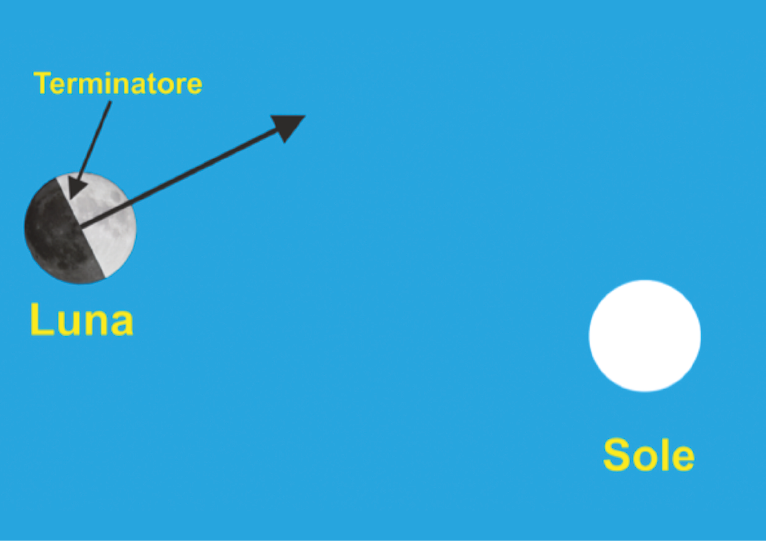
È facile constatare che, quando la Luna non è piena, esiste una forte illusione relativa al margine che separa la sua parte illuminata da quella in ombra, cioè a quello che gli astronomi chiamano terminatore. 
Per semplici ragioni geometriche, la linea retta perpendicolare al centro del terminatore deve passare per il centro del Sole. Se ne può avere la conferma illuminando con una lampadina un oggetto sferico: la retta ortogonale al bordo d’ombra della sfera passerà per il centro della lampadina. Non è però questo che si vede nel caso della Luna e del Sole: quando i due astri sono contemporaneamente visibili nel cielo, la linea ortogonale al terminatore sembra puntare molto al di sopra del Sole, come si illustra nella figura 1.
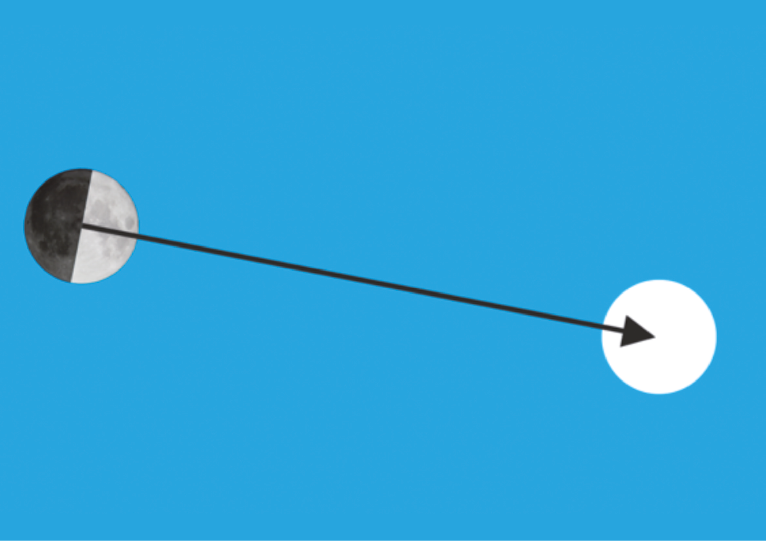
In questa figura si vede subito che non è possibile che una fonte di luce come quella di destra possa creare un terminatore come quello di sinistra, eppure è proprio questo che si vede. L’inclinazione “corretta” del bordo d’ombra è naturalmente quella illustrata nella Figura 2. Il fenomeno in questione, dunque, sembra provare che la Luna non è illuminata dal Sole. 
L’illusione è molto forte. Nell'unica ricerca empirica esistente, N. Schölkopf (1998) l’ha quantificata, nelle sue condizioni, in 12°, ma è facile convincersi, osservando il cielo, che essa è spesso molto maggiore.
Come sostiene lo psicologo S. Anstis (1991), la probabile spiegazione del fenomeno si basa su due fatti, di cui il primo oggettivo e il secondo soggettivo:
1. il Sole e la Luna si trovano a distanze molto diverse dalla Terra: la distanza media del Sole è di circa 150 milioni di km, mentre quella della Luna è di circa 384.000 km. Tuttavia,
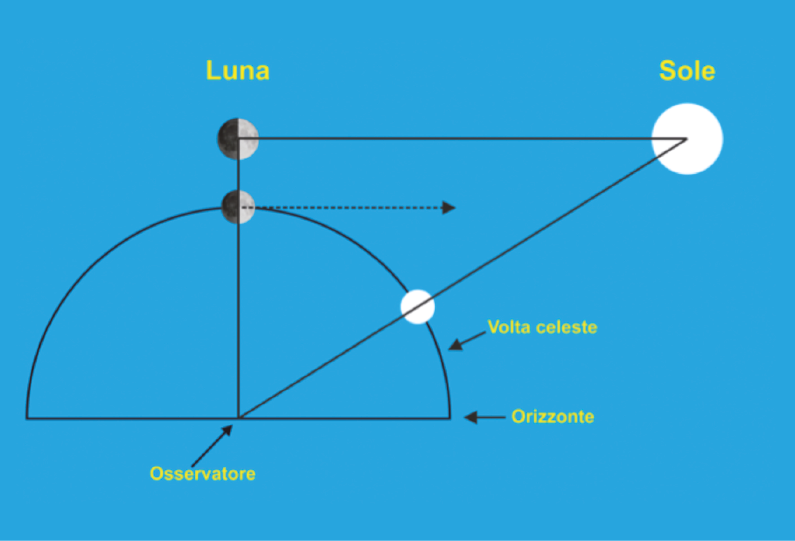
2. i due astri sembrano trovarsi più o meno alla stessa distanza da noi, collocati sulla volta celeste. 
Nella figura 3[3] si mostra come la combinazione di questi due fatti causa l'illusione. Se Sole e Luna fossero percepiti nelle loro reali posizioni nello spazio 3D, una linea ortogonale al centro del terminatore verrebbe correttamente vista passare per il centro del Sole, com’è illustrato nella parte superiore della figura; visto però che noi percepiamo la proiezione dei due corpi sulla volta celeste, tale linea deve necessariamente essere vista passare al di sopra del Sole, com’è illustrato nella parte inferiore della figura.
Sole e Luna sembrano alla stessa distanza perché in cielo non ci sono informazioni che consentano al nostro sistema visivo di stabilire che essi sono, in realtà, a distanze molto diverse. Probabilmente, Sole e Luna non sembrerebbero equidistanti se avessero grandezze angolari diverse, celeste, tale linea di due oggetti viene percepito più lontano (indizio della grandezza relativa), ma per una strana e fuorviante coincidenza Sole e Luna hanno quasi esattamente la stessa grandezza angolare, per cui questa è una ragione in più per percepirli alla stessa distanza. 
Ho trovato l’illusione del terminatore descritta da due soli astronomi: R. A. Proctor (1882) e M. G. J. Minnaert (1993). Non sono un astronomo, e quindi non so se gli addetti ai lavori abbiano ben presente il fenomeno, magari al punto di considerarlo una banalità. Sta di fatto che, quando Anstis (1991) lo descrisse a un matematico, un fisico e un astronomo, nessuno di loro fu in grado, sul momento, di spiegarlo correttamente.
Mi sembra quasi necessario pensare, però, che l’illusione fosse già nota e fosse anche già stata spiegata nell’antichità. Finché si credeva che la Luna splendesse di luce propria, il fatto che una linea perpendicolare al suo terminatore non sembrasse passare per il centro del Sole non costituiva un problema; ma una volta ipotizzato che la Luna riflette la luce solare, non si poteva evitare di confrontarsi, mi pare, con l’evidenza percettiva contraria all’ipotesi, ossia con l’illusione del terminatore, e solo dopo averla spiegata ci si poteva sentire autorizzati a concludere che, contrariamente a ciò che si vede, la Luna è illuminata dal Sole.
Mi pare verosimile, quindi, che il problema fosse già stato affrontato, e probabilmente risolto, da Anassagora, se è vero che fu egli il primo a proporre che la Luna splende di luce solare riflessa. È vero che, per quanto ne so, di tale antica scoperta non ci è giunta notizia esplicita, ma ciò potrebbe essere dovuto al fatto che le fonti dell’epoca sono molto lacunose.
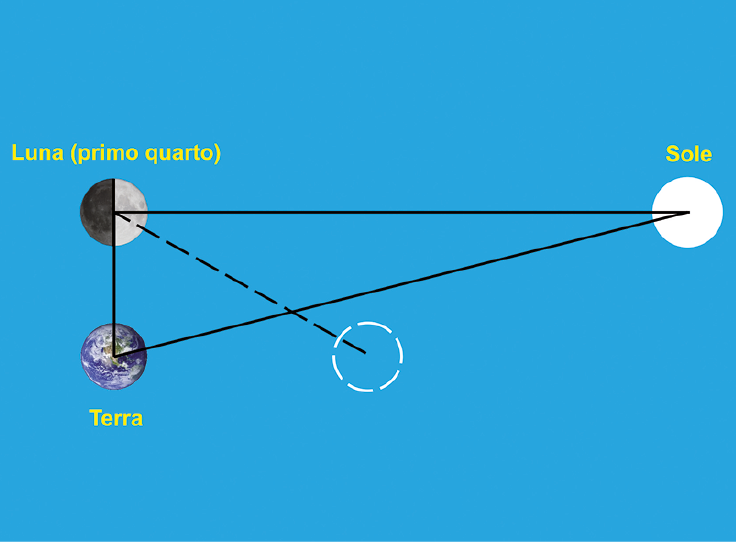
In ogni caso, mi pare ci siano buone ragioni per pensare che del fenomeno in questione, e della sua spiegazione, fosse consapevole Aristarco di Samo (circa 310– 230 a.C.). Nella sua unica opera giunta fino a noi, Aristarco (1913) cercò di stabilire le dimensioni e le distanze del Sole e della Luna. A questo scopo, si servì di alcune ipotesi implicanti tra le altre cose che, quando la Luna è al primo quarto in meridiano e il suo terminatore è verticale, una linea perpendicolare a quest'ultimo passa per il centro del Sole (figura 4)[4]. Come si è visto, ciò è vero, ma sembra clamorosamente smentito dall’illusione del terminatore, a causa della quale, nelle condizioni illustrate nella figura 4, il Sole sembra trovarsi più o meno nella posizione indicata dal cerchio tratteggiato. È impensabile che Aristarco non l’abbia notato, per cui mi pare probabile che egli dovesse conoscere non solo l'illusione in questione ma anche la sua spiegazione, perché altrimenti non avrebbe mai sostenuto che, nelle condizioni suddette, la linea ortogonale al terminatore passa per il centro del Sole.
Si pensi ad esempio alle fasi lunari. Si riuscì a spiegarle, naturalmente, solo quando si arrivò a capire che la Luna splende perché è illuminata dal Sole. Pare che il primo a comprenderlo sia stato Anassagora (vissuto circa dal 510 al 428 a.C.), ma chi venne prima di lui credeva che la Luna brillasse di luce propria[1]. In effetti, le ragioni per pensare che la Luna rifletta la luce solare non sono molte[2], anche perché la vediamo splendere anche di notte, quando in cielo il Sole non c’è. La percezione visiva non suggerisce la risposta giusta; anzi, è legittimo il sospetto che essa abbia ritardato la scoperta della verità. Infatti, c’è almeno un fenomeno, che non ho trovato discusso nella letteratura a me nota sulla storia dell’astronomia, che sembra dimostrare in modo apparentemente incontrovertibile che la Luna non è illuminata dal Sole. Chiamerò tale fenomeno “illusione del terminatore”.
È facile constatare che, quando la Luna non è piena, esiste una forte illusione relativa al margine che separa la sua parte illuminata da quella in ombra, cioè a quello che gli astronomi chiamano terminatore.
Figura 1
In questa figura si vede subito che non è possibile che una fonte di luce come quella di destra possa creare un terminatore come quello di sinistra, eppure è proprio questo che si vede. L’inclinazione “corretta” del bordo d’ombra è naturalmente quella illustrata nella Figura 2. Il fenomeno in questione, dunque, sembra provare che la Luna non è illuminata dal Sole.
Figura 2
Come sostiene lo psicologo S. Anstis (1991), la probabile spiegazione del fenomeno si basa su due fatti, di cui il primo oggettivo e il secondo soggettivo:
1. il Sole e la Luna si trovano a distanze molto diverse dalla Terra: la distanza media del Sole è di circa 150 milioni di km, mentre quella della Luna è di circa 384.000 km. Tuttavia,
2. i due astri sembrano trovarsi più o meno alla stessa distanza da noi, collocati sulla volta celeste.
Figura 3
Sole e Luna sembrano alla stessa distanza perché in cielo non ci sono informazioni che consentano al nostro sistema visivo di stabilire che essi sono, in realtà, a distanze molto diverse. Probabilmente, Sole e Luna non sembrerebbero equidistanti se avessero grandezze angolari diverse, celeste, tale linea di due oggetti viene percepito più lontano (indizio della grandezza relativa), ma per una strana e fuorviante coincidenza Sole e Luna hanno quasi esattamente la stessa grandezza angolare, per cui questa è una ragione in più per percepirli alla stessa distanza.
Figura 4
Mi sembra quasi necessario pensare, però, che l’illusione fosse già nota e fosse anche già stata spiegata nell’antichità. Finché si credeva che la Luna splendesse di luce propria, il fatto che una linea perpendicolare al suo terminatore non sembrasse passare per il centro del Sole non costituiva un problema; ma una volta ipotizzato che la Luna riflette la luce solare, non si poteva evitare di confrontarsi, mi pare, con l’evidenza percettiva contraria all’ipotesi, ossia con l’illusione del terminatore, e solo dopo averla spiegata ci si poteva sentire autorizzati a concludere che, contrariamente a ciò che si vede, la Luna è illuminata dal Sole.
Mi pare verosimile, quindi, che il problema fosse già stato affrontato, e probabilmente risolto, da Anassagora, se è vero che fu egli il primo a proporre che la Luna splende di luce solare riflessa. È vero che, per quanto ne so, di tale antica scoperta non ci è giunta notizia esplicita, ma ciò potrebbe essere dovuto al fatto che le fonti dell’epoca sono molto lacunose.
In ogni caso, mi pare ci siano buone ragioni per pensare che del fenomeno in questione, e della sua spiegazione, fosse consapevole Aristarco di Samo (circa 310– 230 a.C.). Nella sua unica opera giunta fino a noi, Aristarco (1913) cercò di stabilire le dimensioni e le distanze del Sole e della Luna. A questo scopo, si servì di alcune ipotesi implicanti tra le altre cose che, quando la Luna è al primo quarto in meridiano e il suo terminatore è verticale, una linea perpendicolare a quest'ultimo passa per il centro del Sole (figura 4)[4]. Come si è visto, ciò è vero, ma sembra clamorosamente smentito dall’illusione del terminatore, a causa della quale, nelle condizioni illustrate nella figura 4, il Sole sembra trovarsi più o meno nella posizione indicata dal cerchio tratteggiato. È impensabile che Aristarco non l’abbia notato, per cui mi pare probabile che egli dovesse conoscere non solo l'illusione in questione ma anche la sua spiegazione, perché altrimenti non avrebbe mai sostenuto che, nelle condizioni suddette, la linea ortogonale al terminatore passa per il centro del Sole.
Note
1) Heath (1913 e 1932).
2) Ma ne esiste almeno una: come notò Parmenide, la parte luminosa della Luna è sempre rivolta verso il Sole.
3) Le distanze di Sole e Luna non sono in scala, per cui il Sole è rappresentato molto più distante dall’orizzonte di quanto in realtà non sia quando la Luna è al primo quarto in meridiano. Molto più simile alla situazione reale è quella rappresentata nella parte tratteggiata della figura 4.
4) Per una spiegazione di come Aristarco tentò di calcolare la distanza di Sole e Luna a partire dalla situazione rappresentata nella figura 4 si vedano ad esempio Couprie (2011) e questa pagina web: http://tinyurl.com/qa6oo8g. Per una discussione più tecnica si veda Heath (1913).
Bibliografia
- Anstis, S. (1991). Hidden assumptions in seeing shape from shading and
- Aristarco (1913). On the Sizes and Distances of the Sun and Moon. In: T. L. Heath (a cura di), 1913, op. cit., pp. 351-413
- Couprie, D. L. (2011). Heaven and Earth in Ancient Greek Cosmology. From Thales to Heraclides Ponticus, New York: Springer
- Heath, T. L. (a cura di) (1913). Aristarchus of Samos. The Ancient Copernicus, Oxford: Clarendon Press
- Heath, T. L. (1932). Greek Astronomy, New York: Dover
- Hoskin, M. (a cura di) (2001). Storia dell’astronomia di Cambridge, Milano: RCS libri
- Minnaert, M. G. J. (1993). Light and Color in the Outdoors, Springer-Verlag, New York
- Proctor, R. A. (1881). Nota in calce all’articolo “A lunar illusion”. Knowledge, 1, p. 57
- Schölkopf, N. (1998). The moon tilt illusion. Perception, 27, pp. 1229-1232
