L’informazione ha una grande importanza nella nostra vita. Fornisce i parametri mediante i quali leggiamo il mondo che ci circonda, contribuisce a formare la nostra opinione e ci orienta ad agire in un modo piuttosto che in un altro.
Può capitare, tuttavia, di incappare in articoli nei quali espressioni tecniche, specie di carattere scientifico, sono usate impropriamente.
Quante volte ci è successo di sentire o di leggere l’espressione “crescita esponenziale”?
Provate a fare un giro in rete...
«Eolico in crescita esponenziale, in 40 anni crescerà di nove volte». Corriere della Sera, marzo 20, 2014
«Mendicanti in crescita esponenziale». Il Giornale, ottobre 14, 2011
«Negli ultimi 10 anni riscaldamento globale in crescita esponenziale». Wired, febbraio 11, 2016
«Crowdfunding: un fenomeno in crescita esponenziale». Il Fatto Quotidiano, ottobre 6, 2016
Come testimoniano queste citazioni, l’espressione crescita esponenziale viene usata spesso senza cognizione di causa. Nell’immaginario comune, infatti, l’espressione crescita esponenziale è spesso associata al concetto di crescita veloce.
Mi dispiace dover fare la parte della guastafeste, ma tale convinzione è errata.
Scrivere per esempio: «Boom di presenze. Che la location sia uno straordinario punto di forza lo provano i numeri, cresciuti in maniera esponenziale da quando il festival è tornato dentro la città»[1] vorrebbe dire che ad oggi, al festival oggetto dell’articolo, si registrerebbero qualche miliardo di presenze, una affermazione chiaramente inverosimile.
Cerchiamo di capire perché l’uso di questa espressione per indicare una crescita veloce è sbagliato da un punto di vista matematico.
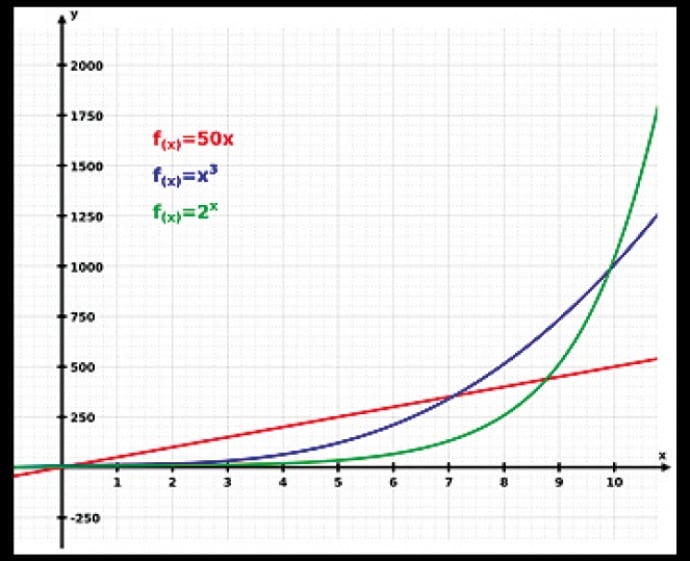
Forse non tutti sanno che esistono differenti funzioni di crescita. Fra le tante, citiamo come esempio:
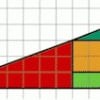
Come si può leggere dal grafico, non in tutti i punti la crescita esponenziale è la funzione di crescita più veloce. Inizialmente, per esempio, sia la crescita lineare che quella cubica possono risultare più veloci della crescita esponenziale.
I fenomeni sottoposti ad una legge di crescita esponenziale non sono infatti caratterizzati da una crescita veloce. Al contrario, in una prima fase si osserva una crescita piuttosto lenta, che poi subisce un’accelerazione improvvisa (la potremmo definire “esplosiva”) la quale è spesso causa di cambiamenti repentini, oltre le aspettative.
Vi racconterò una storiella, simpatica, narrata in tutte le facoltà di matematica e statistica per rendere visivo il concetto di crescita esponenziale.
Narra la leggenda che all’inventore degli scacchi, che presentava in dono al re di Persia il suo nuovo gioco, venne chiesto cosa voleva in cambio del suo regalo. Egli chiese soltanto del riso e disse che la quantità si doveva calcolare mettendo un chicco di riso nella prima casella della scacchiera, 2 chicchi nella seconda, 4 nella terza, 8 nella quarta, e così via, in modo da mettere in ogni casella il doppio dei chicchi messi nella casella precedente. Il simpaticone chiese poi che gli fosse consegnato il contenuto della 64-esima casella. Il re acconsentì prontamente e chiese che fosse portato il riso, rimanendo allibito quando i suoi esperti lo informarono che la quantità di riso richiesta superava di gran lunga le risorse del suo impero! Facciamo un piccolo calcolo. Stimando in 1/45 di grammo il peso medio di un chicco di riso, il peso di 263 chicchi (quelli che dovrebbero trovarsi nella 64-esima casella) è di oltre 200 miliardi di tonnellate. Considerando che la produzione mondiale di riso nel 2014 è stata di 741 milioni di tonnellate, capiamo che evidentemente il re non poté soddisfare tale richiesta[2].
Questa è la vera caratteristica di un fenomeno sottoposto a crescita esponenziale: più è grande la quantità di cui si dispone, più essa si accresce. Se la quantità è piccola aumenta poco, se è media aumenta moderatamente, se è grande aumenta molto.
Vediamo il concetto da un punto di vista prettamente matematico: una funzione esponenziale è una funzione in cui la variabile indipendente (x) compare ad esponente.
a differenza di quanto accade in una funzione lineare in cui la variabile indipendente ricopre un ruolo di fattore moltiplicativo
In particolare, quando si parla di crescita esponenziale nel tempo (t) si parla di qualcosa che, col passare del tempo, cresce in misura esponenziale.
dove a è il valore iniziale di x, cioè x(0) = a, la costante b è un fattore di crescita positivo e ῑ è il tempo richiesto affinchè x aumenti di un fattore di b:
In altre parole, si dice che una grandezza cresce esponenzialmente quando ad intervalli di tempo uguali corrispondono incrementi pari ad una frazione costante del totale.
Se ῑ > 0 e b > 1 allora x ha crescita esponenziale.
Se ῑ < 0 e b < 1 oppure ῑ > 0 e 0 < b < 1 allora x ha decadimento esponenziale[3].
E dal momento che il tempo non smette mai di crescere, questo vuol dire che quella cosa che “cresce in maniera esponenziale” tende a diventare infinita.
L’evidente impossibilità che si verifichi questa conseguenza (almeno sulla Terra) dovrebbe essere sufficiente perché ci si convinca dell’uso improprio di tale espressione.
Tuttavia, ciò che andrebbe tenuto presente quando si usa l’aggettivo “esponenziale” è che certi fenomeni possono essere caratterizzati da una crescita esponenziale, ma solo per un determinato, limitato, periodo di tempo. Per esempio, in biologia, il numero di microrganismi in un brodo di coltura crescerà esponenzialmente fino a quando non sarà esaurito il nutriente essenziale. Il primo organismo si divide in due organismi figli, che poi si dividono per formarne quattro, che a loro volta si dividono per formarne otto, e così via. In fisica, nella reazione nucleare a catena (il fenomeno dietro le armi nucleari), ogni nucleo di uranio che subisce la scissione produce neutroni multipli, ciascuno dei quali può essere assorbito dagli adiacenti nuclei di uranio, facendo sì che essi si scindano a loro volta. Se la probabilità di assorbimento dei neutroni supera la probabilità di fuga dei neutroni stessi, il tasso di produzione dei neutroni e di scissioni di uranio indotte aumenta esponenzialmente, in una reazione incontrollata. In economia, l’interesse composto a un tasso d’interesse costante fornisce la crescita esponenziale del capitale. Come ultimo esempio, nell’informatica la teoria della complessità computazionale prevede che gli algoritmi di complessità esponenziale dei computer richiedono un ammontare di risorse esponenzialmente crescente (ad es. tempo, memoria del computer) a fronte di un aumento costante della dimensione dei problemi[4].
Un modo per illustrare l’estrema rapidità con la quale una crescita esponenziale porta ad approssimarsi ad un valore prefissato è quella di fare ricorso ad un indovinello per bambini. Immaginiamo di avere uno stagno con una pianta di ninfea, le cui foglie galleggiano sulla superficie. La ninfea raddoppia di dimensione ogni giorno e se lasciata incontrollata soffocherà lo stagno in 30 giorni, uccidendo tutte le altre cose viventi nell'acqua. Giorno dopo giorno la pianta sembra piccola e così si decide di lasciarla crescere fino a quando non ricoprirà metà dello stagno, prima di tagliarla. Volendo salvare lo stagno dall’invasione delle foglie di ninfea, in quale giorno si dovrebbe intervenire?
La risposta è al 29° giorno, cioè nell’arco di un’unica giornata la situazione passerebbe da rimediabile a irreparabile. Il risultato è sorprendente soprattutto se si riflette sul fatto che il 25° giorno lo stagno risulta essere coperto per poco più del 3% della sua superficie.
Anche se spesso le nostre interazioni quotidiane con i numeri sono frettolose e superficiali, questi ricoprono un ruolo importante nella nostra vita. Riuscire a valutare gli ordini di grandezza dei fenomeni ci aiuta a guardare più oggettivamente le nostre esperienze nonché la realtà di cui facciamo parte. Saper cogliere la differenza fra il titolo sensazionalistico di un quotidiano e ciò che veramente è rappresentato dai numeri che vengono illustrati è un primo piccolo passo per non crearsi idee sbagliate ed essere più consapevoli del mondo in cui viviamo.
Citando Kenneth Ewart Boulding (economista, pacifista e poeta inglese): “Chi crede che una crescita esponenziale possa continuare all’infinito in un mondo finito è un folle”[5].
Può capitare, tuttavia, di incappare in articoli nei quali espressioni tecniche, specie di carattere scientifico, sono usate impropriamente.
Quante volte ci è successo di sentire o di leggere l’espressione “crescita esponenziale”?
Provate a fare un giro in rete...
«Eolico in crescita esponenziale, in 40 anni crescerà di nove volte». Corriere della Sera, marzo 20, 2014
«Mendicanti in crescita esponenziale». Il Giornale, ottobre 14, 2011
«Negli ultimi 10 anni riscaldamento globale in crescita esponenziale». Wired, febbraio 11, 2016
«Crowdfunding: un fenomeno in crescita esponenziale». Il Fatto Quotidiano, ottobre 6, 2016
Come testimoniano queste citazioni, l’espressione crescita esponenziale viene usata spesso senza cognizione di causa. Nell’immaginario comune, infatti, l’espressione crescita esponenziale è spesso associata al concetto di crescita veloce.
Mi dispiace dover fare la parte della guastafeste, ma tale convinzione è errata.
Scrivere per esempio: «Boom di presenze. Che la location sia uno straordinario punto di forza lo provano i numeri, cresciuti in maniera esponenziale da quando il festival è tornato dentro la città»[1] vorrebbe dire che ad oggi, al festival oggetto dell’articolo, si registrerebbero qualche miliardo di presenze, una affermazione chiaramente inverosimile.
Cerchiamo di capire perché l’uso di questa espressione per indicare una crescita veloce è sbagliato da un punto di vista matematico.
Forse non tutti sanno che esistono differenti funzioni di crescita. Fra le tante, citiamo come esempio:
- - crescita lineare (in rosso nel grafico)
- - crescita cubica (in blu)
- - crescita esponenziale (in verde)
Come si può leggere dal grafico, non in tutti i punti la crescita esponenziale è la funzione di crescita più veloce. Inizialmente, per esempio, sia la crescita lineare che quella cubica possono risultare più veloci della crescita esponenziale.
I fenomeni sottoposti ad una legge di crescita esponenziale non sono infatti caratterizzati da una crescita veloce. Al contrario, in una prima fase si osserva una crescita piuttosto lenta, che poi subisce un’accelerazione improvvisa (la potremmo definire “esplosiva”) la quale è spesso causa di cambiamenti repentini, oltre le aspettative.
Vi racconterò una storiella, simpatica, narrata in tutte le facoltà di matematica e statistica per rendere visivo il concetto di crescita esponenziale.
Narra la leggenda che all’inventore degli scacchi, che presentava in dono al re di Persia il suo nuovo gioco, venne chiesto cosa voleva in cambio del suo regalo. Egli chiese soltanto del riso e disse che la quantità si doveva calcolare mettendo un chicco di riso nella prima casella della scacchiera, 2 chicchi nella seconda, 4 nella terza, 8 nella quarta, e così via, in modo da mettere in ogni casella il doppio dei chicchi messi nella casella precedente. Il simpaticone chiese poi che gli fosse consegnato il contenuto della 64-esima casella. Il re acconsentì prontamente e chiese che fosse portato il riso, rimanendo allibito quando i suoi esperti lo informarono che la quantità di riso richiesta superava di gran lunga le risorse del suo impero! Facciamo un piccolo calcolo. Stimando in 1/45 di grammo il peso medio di un chicco di riso, il peso di 263 chicchi (quelli che dovrebbero trovarsi nella 64-esima casella) è di oltre 200 miliardi di tonnellate. Considerando che la produzione mondiale di riso nel 2014 è stata di 741 milioni di tonnellate, capiamo che evidentemente il re non poté soddisfare tale richiesta[2].
Questa è la vera caratteristica di un fenomeno sottoposto a crescita esponenziale: più è grande la quantità di cui si dispone, più essa si accresce. Se la quantità è piccola aumenta poco, se è media aumenta moderatamente, se è grande aumenta molto.
Vediamo il concetto da un punto di vista prettamente matematico: una funzione esponenziale è una funzione in cui la variabile indipendente (x) compare ad esponente.
- y = b^x
a differenza di quanto accade in una funzione lineare in cui la variabile indipendente ricopre un ruolo di fattore moltiplicativo
- y = b • x
In particolare, quando si parla di crescita esponenziale nel tempo (t) si parla di qualcosa che, col passare del tempo, cresce in misura esponenziale.
- x(t) = a • b^(t/ῑ)
dove a è il valore iniziale di x, cioè x(0) = a, la costante b è un fattore di crescita positivo e ῑ è il tempo richiesto affinchè x aumenti di un fattore di b:
- x(t + ῑ) = x(t) • b
In altre parole, si dice che una grandezza cresce esponenzialmente quando ad intervalli di tempo uguali corrispondono incrementi pari ad una frazione costante del totale.
Se ῑ > 0 e b > 1 allora x ha crescita esponenziale.
Se ῑ < 0 e b < 1 oppure ῑ > 0 e 0 < b < 1 allora x ha decadimento esponenziale[3].
E dal momento che il tempo non smette mai di crescere, questo vuol dire che quella cosa che “cresce in maniera esponenziale” tende a diventare infinita.
L’evidente impossibilità che si verifichi questa conseguenza (almeno sulla Terra) dovrebbe essere sufficiente perché ci si convinca dell’uso improprio di tale espressione.
Tuttavia, ciò che andrebbe tenuto presente quando si usa l’aggettivo “esponenziale” è che certi fenomeni possono essere caratterizzati da una crescita esponenziale, ma solo per un determinato, limitato, periodo di tempo. Per esempio, in biologia, il numero di microrganismi in un brodo di coltura crescerà esponenzialmente fino a quando non sarà esaurito il nutriente essenziale. Il primo organismo si divide in due organismi figli, che poi si dividono per formarne quattro, che a loro volta si dividono per formarne otto, e così via. In fisica, nella reazione nucleare a catena (il fenomeno dietro le armi nucleari), ogni nucleo di uranio che subisce la scissione produce neutroni multipli, ciascuno dei quali può essere assorbito dagli adiacenti nuclei di uranio, facendo sì che essi si scindano a loro volta. Se la probabilità di assorbimento dei neutroni supera la probabilità di fuga dei neutroni stessi, il tasso di produzione dei neutroni e di scissioni di uranio indotte aumenta esponenzialmente, in una reazione incontrollata. In economia, l’interesse composto a un tasso d’interesse costante fornisce la crescita esponenziale del capitale. Come ultimo esempio, nell’informatica la teoria della complessità computazionale prevede che gli algoritmi di complessità esponenziale dei computer richiedono un ammontare di risorse esponenzialmente crescente (ad es. tempo, memoria del computer) a fronte di un aumento costante della dimensione dei problemi[4].
Un modo per illustrare l’estrema rapidità con la quale una crescita esponenziale porta ad approssimarsi ad un valore prefissato è quella di fare ricorso ad un indovinello per bambini. Immaginiamo di avere uno stagno con una pianta di ninfea, le cui foglie galleggiano sulla superficie. La ninfea raddoppia di dimensione ogni giorno e se lasciata incontrollata soffocherà lo stagno in 30 giorni, uccidendo tutte le altre cose viventi nell'acqua. Giorno dopo giorno la pianta sembra piccola e così si decide di lasciarla crescere fino a quando non ricoprirà metà dello stagno, prima di tagliarla. Volendo salvare lo stagno dall’invasione delle foglie di ninfea, in quale giorno si dovrebbe intervenire?
La risposta è al 29° giorno, cioè nell’arco di un’unica giornata la situazione passerebbe da rimediabile a irreparabile. Il risultato è sorprendente soprattutto se si riflette sul fatto che il 25° giorno lo stagno risulta essere coperto per poco più del 3% della sua superficie.
Anche se spesso le nostre interazioni quotidiane con i numeri sono frettolose e superficiali, questi ricoprono un ruolo importante nella nostra vita. Riuscire a valutare gli ordini di grandezza dei fenomeni ci aiuta a guardare più oggettivamente le nostre esperienze nonché la realtà di cui facciamo parte. Saper cogliere la differenza fra il titolo sensazionalistico di un quotidiano e ciò che veramente è rappresentato dai numeri che vengono illustrati è un primo piccolo passo per non crearsi idee sbagliate ed essere più consapevoli del mondo in cui viviamo.
Citando Kenneth Ewart Boulding (economista, pacifista e poeta inglese): “Chi crede che una crescita esponenziale possa continuare all’infinito in un mondo finito è un folle”[5].
Note
1) “Fenomeno Comics, Lucca presa d'assalto”. Il Tirreno, ottobre 31, 2015
2) Donella H. Meadows, Dennis L. Meadows, Jørgen Randers, William W. Behrens III. 1972 The Limits to Growth. New York: University Books.
3) Viviana Amati. Approfondimenti sui modelli di crescita. Crescita aritmetica, geometrica, esponenziale. 2009. Edizioni Il Mulino.
4) Enzo Orsingher, Luisa Beghin. Introduzione alla probabilità. 2009. Carocci editore.
5) Silvano Fuso. Pinocchio e la scienza. Come difendersi da false credenze e bufale scientifiche. 2006. Edizioni Dedalo.