Gli errori nel ragionamento logico-matematico possono portare a divertenti risultati paradossali.
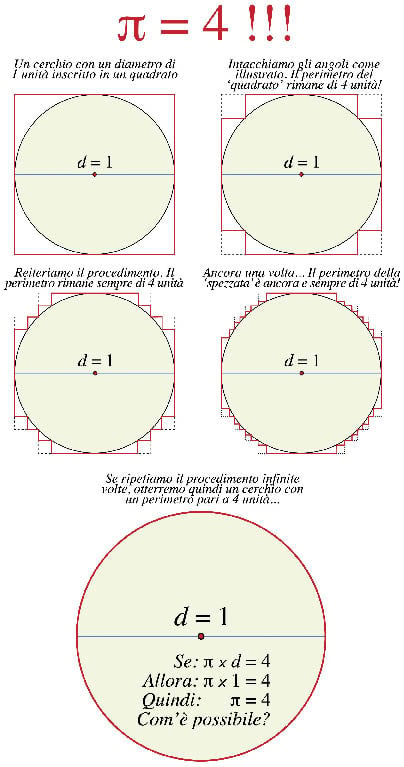
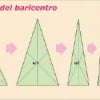
Nella figura 1 sono illustrati alcuni semplici procedimenti che portano alla dimostrazione che il valore di π è pari a 4! Infatti, la “spezzata” che circoscrive il cerchio diventa, man mano che reiteriamo il procedimento, così fine che tenderà alla circonferenza del cerchio. E quindi, ad avvalorare la tesi che π = 4.
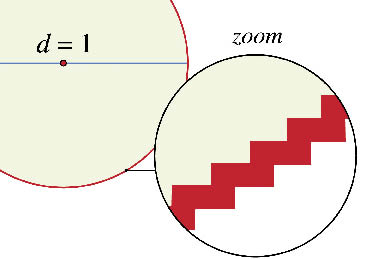
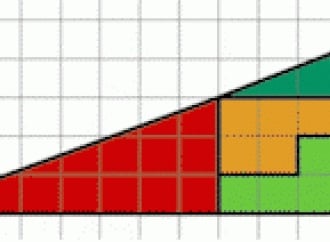
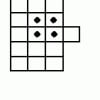
L’errore di questa dimostrazione è davvero subdolo: dipende da cosa intendiamo con “tende”. Il perimetro della spezzata era fisso sin dalla prima iterazione e la sua natura di spezzata rimane tale. Anche se i gradini della spezzata diventano infinitesimali o quasi invisibili a occhio nudo (vedi fig. 2), essi non “copriranno” mai la circonferenza del cerchio.
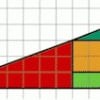
Questo esperimento serve anche a illustrare la differenza tra un disegno vettoriale e un disegno bitmap. Nella grafica vettoriale, un’immagine è descritta mediante un insieme di primitive geometriche che descrivono punti, linee, curve e poligoni. Mentre nella grafica bitmap, l’immagine viene vista come una scacchiera e a ogni elemento della scacchiera, chiamato “pixel”, viene associato uno specifico colore.
Un’immagine vettoriale può essere ingrandita quanto si vuole senza perdere qualità, a differenza di un’immagine bitmap dove i pixel formano a un certo punto delle dentellature (un cerchio disegnato con un software bitmap è, in realtà, dentellato a gradini).
Nella figura 1 sono illustrati alcuni semplici procedimenti che portano alla dimostrazione che il valore di π è pari a 4! Infatti, la “spezzata” che circoscrive il cerchio diventa, man mano che reiteriamo il procedimento, così fine che tenderà alla circonferenza del cerchio. E quindi, ad avvalorare la tesi che π = 4.
Riflettiamo
L’errore di questa dimostrazione è davvero subdolo: dipende da cosa intendiamo con “tende”. Il perimetro della spezzata era fisso sin dalla prima iterazione e la sua natura di spezzata rimane tale. Anche se i gradini della spezzata diventano infinitesimali o quasi invisibili a occhio nudo (vedi fig. 2), essi non “copriranno” mai la circonferenza del cerchio.
Questo esperimento serve anche a illustrare la differenza tra un disegno vettoriale e un disegno bitmap. Nella grafica vettoriale, un’immagine è descritta mediante un insieme di primitive geometriche che descrivono punti, linee, curve e poligoni. Mentre nella grafica bitmap, l’immagine viene vista come una scacchiera e a ogni elemento della scacchiera, chiamato “pixel”, viene associato uno specifico colore.
Un’immagine vettoriale può essere ingrandita quanto si vuole senza perdere qualità, a differenza di un’immagine bitmap dove i pixel formano a un certo punto delle dentellature (un cerchio disegnato con un software bitmap è, in realtà, dentellato a gradini).