In questo articolo mostriamo come la razionalità possa essere utilizzata per pensare fuori dagli schemi e percorrere strade inaspettate per affrontare le sfide che la realtà ci pone di fronte.
Ottimizziamo!
Una classe di problemi molto presenti nella quotidianità del nostro mondo rapido e interconnesso è quella dei problemi di ottimizzazione: valutare il miglior investimento per i nostri risparmi, percorrere la strada più breve o con meno traffico per tornare a casa, mangiare nel miglior ristorante in base a vicinanza-qualità-prezzo, ...
In maniera più generale, fissato un obiettivo che può avere molte strade per essere raggiunto, ottimizzare vuol dire trovare la soluzione più semplice, dove i termini molte strade e semplice possono essere definiti e valutati rigorosamente a livello matematico.
Presentiamo qui due problemi classici in teoria dell’ottimizzazione, entrambi problemi-modello che, con le opportune modifiche, si applicano in molte situazioni di vita reale:
Problema dello zaino, knapsack problem.
Dato un insieme di oggetti, ciascuno dei quali ha un certo peso e un certo valore, come fare una selezione in modo da riempire uno zaino che può reggere solo un certo peso massimo, cercando di portar dietro il valore più alto possibile?
Invitiamo chi legge a cercare una soluzione del semplice esempio in Figura 1 o, meglio, a cercare una strategia di risoluzione del problema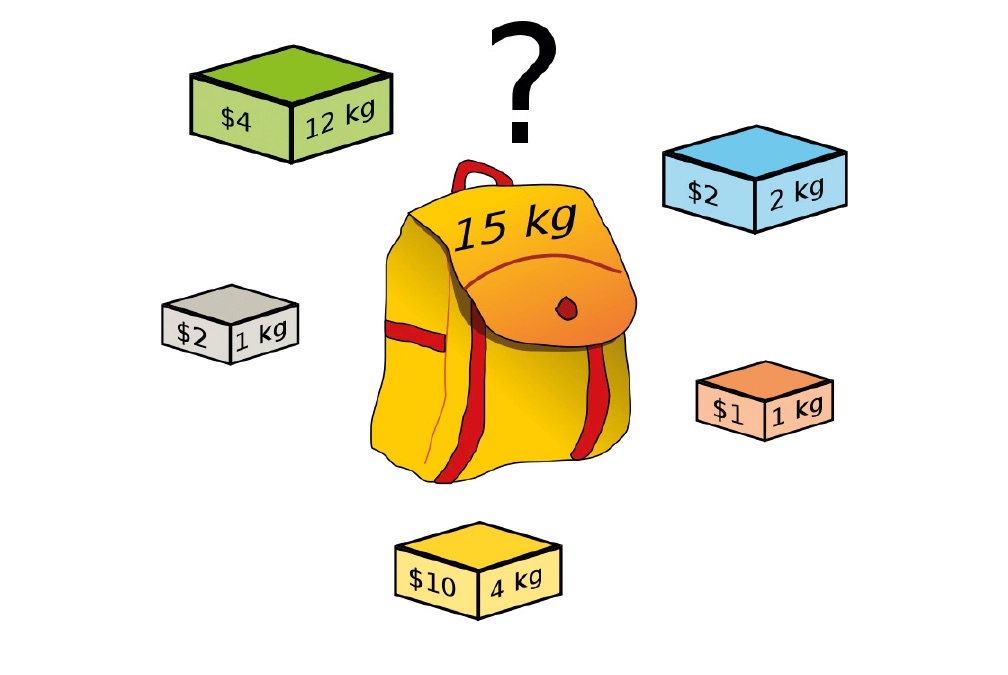 
Problema del commesso viaggiatore, Travelling Salesman Problem (TSP).
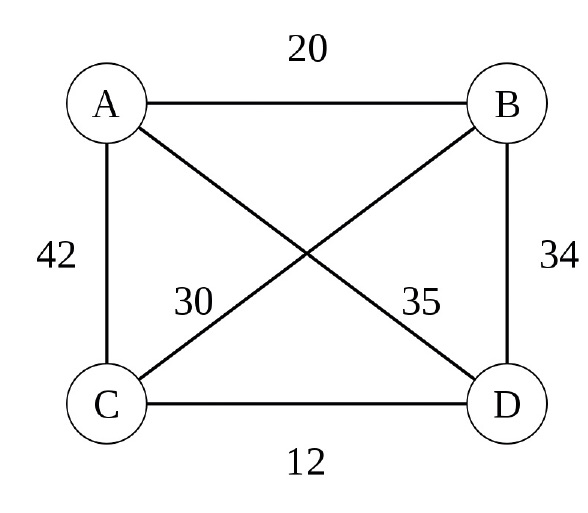Dato un territorio in cui sono presenti un gran numero di città, ciascuna in una posizione specifica, qual è il percorso più breve che consente di visitare ogni città esattamente una volta per poi tornare alla città iniziale?
Anche in questo caso, prima di proseguire consigliamo di provare a trovare strategie risolutive per il caso semplice in Figura 2.
Nel seguito scegliamo come problema di riferimento proprio il TSP, che ha lampanti applicazioni pratiche, dato che immagino siano venuti in mente a tutti i corrieri di Amazon.
Come affrontare tale problema? Come scegliere un buon algoritmo?
Una prima e ragionevole scelta potrebbe essere la forza bruta, o ricerca esaustiva: le possibili strade sono tante, ma non sono certo infinite. Allora perché non calcolarle tutte, per poi scegliere la migliore? Viviamo nel ventunesimo secolo, i calcoli non verranno certamente fatti a mano, e i computer sono veloci. Il ragionamento fila in maniera teorica, ma la realtà ci si pone immediatamente davanti come un muro invalicabile: l’insieme dei percorsi possibili per un problema con un numero sufficiente di città è troppo grande, così grande che la risoluzione impiegherebbe il più potente dei computer per millenni. Bisogna utilizzare strategie diverse.
La teoria dell’ottimizzazione e della ricerca operativa ci spiegano che esistono due strategie di attacco principali per questo tipo di problemi: la ricerca di algoritmi esatti e la ricerca di algoritmi euristici.
Gli algoritmi del primo tipo consistono in una sequenza di passaggi in grado di trovare la soluzione esatta dopo un numero finito di passaggi. Il metodo di forza bruta rientra in questa classe, anticipandone la limitazione principale: alcuni problemi necessitano di troppo tempo per essere risolti esattamente.
C’è alternativa?
Gli algoritmi euristici sono un’alternativa, garantendo soluzioni al problema in tempo minore, ma accontentandosi di soluzioni sub-ottimali. Spesso questo è un buon compromesso: tra avere una soluzione perfetta tra mille anni e avere una soluzione sufficientemente buona in un tempo ragionevole, io, addetto alla logistica per la distribuzione di merci, preferisco la seconda opzione.
Ci sono svariati algoritmi euristici, ciascuno con le sue caratteristiche e motivazioni. Ne presentiamo uno qui di seguito, che mostra come siano stati scandagliati i più disparati ambiti del sapere scientifico al fine di risolvere un problema: parliamo dell’ACO, acronimo di Ant Colony Optimization.
L’ACO, come dice il nome, trae ispirazione dalla biologia delle formiche e si basa sul concetto di superorganismo di un formicaio. Inizialmente proposto nei primi anni '90, si basa sul comportamento delle formiche che cercano un percorso tra la loro colonia e una fonte di cibo.
Supponiamo di trovarci di fronte a una situazione come quella in Figura 3, con il formicaio connesso al cibo solamente da due strade, una più lunga, l’altra ottimale.
Le formiche foraggiatrici cominciano ad uscire e muoversi casualmente fuori dal nido. Con il passare del tempo, alcune arriveranno al cibo passando dalla prima strada, altre dalla seconda e, dopo aver preso un po’ di cibo per la colonia, si dirigeranno nuovamente verso il formicaio, percorrendo la strada al contrario. Tornando indietro, le formiche emettono un feromone particolare, un segnale odoroso capace di attrarre le altre foraggiatrici; queste cominceranno allora a seguire la strada odorosa fino a trovare il cibo e, una volta giunte, lo raccoglieranno per poi tornare indietro emettendo feromoni che attireranno altre foraggiatrici, ...
Qui entra in gioco la componente del gioco più importante: la volatilità del feromone. Dopo un certo tempo l’odore svanisce e le formiche ne sono attratte sempre meno; se non evaporasse, ogni strada che conduce al cibo sarebbe trafficata allo stesso modo perché avrebbe sempre la massima intensità di odore. Se c’è evaporazione, le strade più trafficate saranno quelle più odorose, perché più formiche lasceranno feromoni e, a parità di formiche che percorrono le due strade avanti e indietro, sarà proprio la strada più corta ad essere quella più odorosa. Dopo un po’ di tempo quindi, la maggior parte delle formiche camminerà sulla stessa strada, la strada ottimale.
Bene la lezione di biologia, ma che c’entra il problema del commesso viaggiatore?
Anche se limitatamente alle capacità cognitive della singola formica, la colonia è in grado di trovare il percorso più breve tra due luoghi. Questa è l’idea che si può applicare, trasformata in algoritmo, per risolvere euristicamente dei problemi di ottimizzazione, come il TSP: l’algoritmo generale è basato su un insieme di agenti (le formiche), ciascuno dei quali attraversa un percorso tra quelli possibili. In ogni fase, la formica sceglie di spostarsi da una città all’altra secondo alcune regole:
L’ACO non è l’unico algoritmo di ottimizzazione proposto a partire dalla biologia, si pensi ad esempio agli algoritmi genetici, ispirati alla struttura stessa della teoria dell’Evoluzione, e la teoria dell’ottimizzazione non è l’unica branca della matematica che emula comportamenti naturali. Studiare la Natura, astrarre e utilizzare la conoscenza ottenuta per risolvere problemi di natura più generale è sicuramente uno dei lati più affascinanti del pensiero scientifico, e mostra come la conoscenza sia un unico grande organismo, formato da parti che dialogano tra loro, e non una sterile raccolta di discipline autoreferenziali e indipendenti.
Ottimizziamo!
Una classe di problemi molto presenti nella quotidianità del nostro mondo rapido e interconnesso è quella dei problemi di ottimizzazione: valutare il miglior investimento per i nostri risparmi, percorrere la strada più breve o con meno traffico per tornare a casa, mangiare nel miglior ristorante in base a vicinanza-qualità-prezzo, ...
In maniera più generale, fissato un obiettivo che può avere molte strade per essere raggiunto, ottimizzare vuol dire trovare la soluzione più semplice, dove i termini molte strade e semplice possono essere definiti e valutati rigorosamente a livello matematico.
Presentiamo qui due problemi classici in teoria dell’ottimizzazione, entrambi problemi-modello che, con le opportune modifiche, si applicano in molte situazioni di vita reale:
Problema dello zaino, knapsack problem.
Dato un insieme di oggetti, ciascuno dei quali ha un certo peso e un certo valore, come fare una selezione in modo da riempire uno zaino che può reggere solo un certo peso massimo, cercando di portar dietro il valore più alto possibile?
Invitiamo chi legge a cercare una soluzione del semplice esempio in Figura 1 o, meglio, a cercare una strategia di risoluzione del problema
Figura 1. Quali scatole scegliere per massimizzare il valore in denaro, tenendo conto che lo zaino non può contenere più di 15 chili di materiale? Prima immagina di avere a disposizione un qualunque numero di scatole di ciascun colore, poi di avere a disposizione esclusivamente le scatole mostrate in figura
Problema del commesso viaggiatore, Travelling Salesman Problem (TSP).
Figura 2. Qual è il percorso più breve che collega le quattro città A, B, C, D e che passa per ciascuna città una sola volta, sapendo che A deve essere sia il punto iniziale che finale, e che ciascuna città deve essere visitata una sola volta? I numeri rappresentano i chilometri di distanza.
Anche in questo caso, prima di proseguire consigliamo di provare a trovare strategie risolutive per il caso semplice in Figura 2.
Nel seguito scegliamo come problema di riferimento proprio il TSP, che ha lampanti applicazioni pratiche, dato che immagino siano venuti in mente a tutti i corrieri di Amazon.
Come affrontare tale problema? Come scegliere un buon algoritmo?
Una prima e ragionevole scelta potrebbe essere la forza bruta, o ricerca esaustiva: le possibili strade sono tante, ma non sono certo infinite. Allora perché non calcolarle tutte, per poi scegliere la migliore? Viviamo nel ventunesimo secolo, i calcoli non verranno certamente fatti a mano, e i computer sono veloci. Il ragionamento fila in maniera teorica, ma la realtà ci si pone immediatamente davanti come un muro invalicabile: l’insieme dei percorsi possibili per un problema con un numero sufficiente di città è troppo grande, così grande che la risoluzione impiegherebbe il più potente dei computer per millenni. Bisogna utilizzare strategie diverse.
La teoria dell’ottimizzazione e della ricerca operativa ci spiegano che esistono due strategie di attacco principali per questo tipo di problemi: la ricerca di algoritmi esatti e la ricerca di algoritmi euristici.
Gli algoritmi del primo tipo consistono in una sequenza di passaggi in grado di trovare la soluzione esatta dopo un numero finito di passaggi. Il metodo di forza bruta rientra in questa classe, anticipandone la limitazione principale: alcuni problemi necessitano di troppo tempo per essere risolti esattamente.
C’è alternativa?
Gli algoritmi euristici sono un’alternativa, garantendo soluzioni al problema in tempo minore, ma accontentandosi di soluzioni sub-ottimali. Spesso questo è un buon compromesso: tra avere una soluzione perfetta tra mille anni e avere una soluzione sufficientemente buona in un tempo ragionevole, io, addetto alla logistica per la distribuzione di merci, preferisco la seconda opzione.
Ci sono svariati algoritmi euristici, ciascuno con le sue caratteristiche e motivazioni. Ne presentiamo uno qui di seguito, che mostra come siano stati scandagliati i più disparati ambiti del sapere scientifico al fine di risolvere un problema: parliamo dell’ACO, acronimo di Ant Colony Optimization.
L’ACO, come dice il nome, trae ispirazione dalla biologia delle formiche e si basa sul concetto di superorganismo di un formicaio. Inizialmente proposto nei primi anni '90, si basa sul comportamento delle formiche che cercano un percorso tra la loro colonia e una fonte di cibo.
Figura 3. Il formicaio, in rosso, è collegato al cibo, in nero, da due strade di lunghezza diversa.
Le formiche foraggiatrici cominciano ad uscire e muoversi casualmente fuori dal nido. Con il passare del tempo, alcune arriveranno al cibo passando dalla prima strada, altre dalla seconda e, dopo aver preso un po’ di cibo per la colonia, si dirigeranno nuovamente verso il formicaio, percorrendo la strada al contrario. Tornando indietro, le formiche emettono un feromone particolare, un segnale odoroso capace di attrarre le altre foraggiatrici; queste cominceranno allora a seguire la strada odorosa fino a trovare il cibo e, una volta giunte, lo raccoglieranno per poi tornare indietro emettendo feromoni che attireranno altre foraggiatrici, ...
Qui entra in gioco la componente del gioco più importante: la volatilità del feromone. Dopo un certo tempo l’odore svanisce e le formiche ne sono attratte sempre meno; se non evaporasse, ogni strada che conduce al cibo sarebbe trafficata allo stesso modo perché avrebbe sempre la massima intensità di odore. Se c’è evaporazione, le strade più trafficate saranno quelle più odorose, perché più formiche lasceranno feromoni e, a parità di formiche che percorrono le due strade avanti e indietro, sarà proprio la strada più corta ad essere quella più odorosa. Dopo un po’ di tempo quindi, la maggior parte delle formiche camminerà sulla stessa strada, la strada ottimale.
Bene la lezione di biologia, ma che c’entra il problema del commesso viaggiatore?
Anche se limitatamente alle capacità cognitive della singola formica, la colonia è in grado di trovare il percorso più breve tra due luoghi. Questa è l’idea che si può applicare, trasformata in algoritmo, per risolvere euristicamente dei problemi di ottimizzazione, come il TSP: l’algoritmo generale è basato su un insieme di agenti (le formiche), ciascuno dei quali attraversa un percorso tra quelli possibili. In ogni fase, la formica sceglie di spostarsi da una città all’altra secondo alcune regole:
- più una città è distante, meno possibilità ha di essere scelta;
- più l’intensità del feromone situato sulla strada tra due città è alta, maggiore è la probabilità che tale strada sia scelta;
- una volta completato il suo percorso, la formica deposita, su tutta la strada attraversata, una certa quantità di feromone, maggiore se il percorso è stato breve;
- i percorsi di feromone evaporano ad ogni iterazione dell’algoritmo.
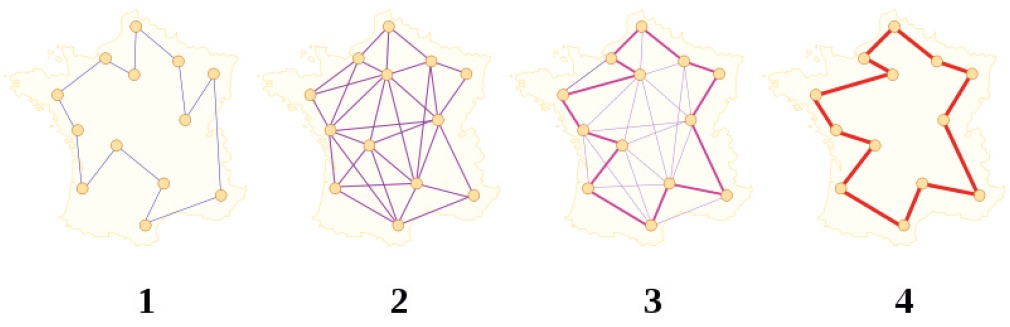
Figura 4. Soluzione tramite ACO del problema del commesso viaggiatore: 1. una formica sceglie un percorso tra i possibili e lascia una traccia di feromone su di esso; 2. tutte le formiche percorrono varie strade, lasciando traccia di feromone in base alla qualità della soluzione che hanno trovato (più corta la strada, maggiore la quantità di feromone); 3. gli archi del percorso migliore risulteranno più odorosi (rinforzati) degli altri; 4. la volatilità del feromone assicura che le soluzioni peggiori col tempo svaniscano.
L’ACO non è l’unico algoritmo di ottimizzazione proposto a partire dalla biologia, si pensi ad esempio agli algoritmi genetici, ispirati alla struttura stessa della teoria dell’Evoluzione, e la teoria dell’ottimizzazione non è l’unica branca della matematica che emula comportamenti naturali. Studiare la Natura, astrarre e utilizzare la conoscenza ottenuta per risolvere problemi di natura più generale è sicuramente uno dei lati più affascinanti del pensiero scientifico, e mostra come la conoscenza sia un unico grande organismo, formato da parti che dialogano tra loro, e non una sterile raccolta di discipline autoreferenziali e indipendenti.
Riferimenti bibliografici
- Ant Colony Optimization, M. Dorigo, T. Stützle, MIT Press, 2004.
- Imagine Math 2. Between Culture and Mathematics, a cura di Michele Emmer, Springe, Verlag Italia, 2013.
- Il superorganismo, B. Holldobler, E.O. Wilson, Adelphi, 2011.
- Figure 1,2,4 da Wikipedia.org
