Coriandoli infiniti
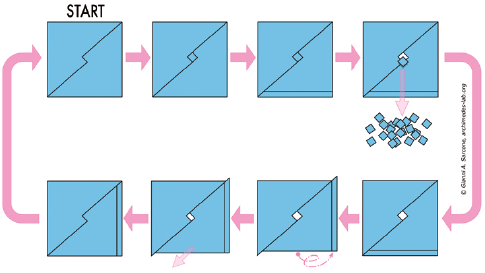
Si può far materializzare dal nulla e in modo infinito degli oggetti? Sì, con un trucco geometrico di nostra invenzione. In questo giochino, abbiamo appunto abbinato moto perpetuo e magia! Occorre quindi un semplice foglio di carta quadrato, che ritaglieremo in tre pezzi distinti, seguendo una procedura per tappe che ci consentirà di produrre all’infinito coriandoli dal nulla. Come potete notare dalle indicazioni illustrate qui sotto, il gioco si ripete all’infinito in modo ciclico.
Qual è il trucco?
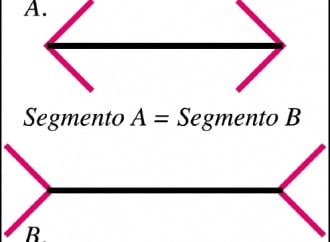
Ingannare la nostra percezione: la soluzione si trova nella spartizione del quadrato e nella ridistribuzione del ‘vuoto’. Una volta riformata, la figura iniziale sembra essere uguale a quella con il buco. Ma - c’è sempre un ‘ma’ -, se si potesse sovrapporre il quadrato iniziale sul quadrato con il buco, si noterebbe una piccola differenza nell’altezza. Il quadrato iniziale è, difatti, leggermente più corto, anche se in maniera infinitesimale. Questa differenza moltiplicata per il lato del quadrato rappresenta l’area sottratta al quadratino rimosso (il coriandolo) e allo spazio tra le giunture dei pezzi riuniti.
Quindi, come sentenziò Lavoisier, nulla scompare o appare dal nulla!
Per saperne di più
Abbiamo presentato un gioco simile col nome “sofisma geometrico” nel numero 8 di Query (pagina 47).
Per visionare la versione animata del gioco, visitate questo link: http://goo.gl/3r9dVQ
Qui, invece, troverete una divertente variante (“enigma della cioccolata” di Mariano Tomatis): http://goo.gl/ZzYbH6