Osservate attentamente le due foto in fig. 1.a e b del Duomo di Firenze e confrontate tra loro la pendenza della facciata e della torre... Bene, sapete dire se l’angolazione dello scatto è identica o diversa? Allo stesso modo, osservate e confrontate le immagini nelle fig. 2.a e b che rappresentano una strada in salita. Secondo voi sono identiche?
Il Duomo di Firenze in fig. 1.a e la strada in fig. 2.b sembrano avere una maggiore pendenza della loro controparte, sebbene siano perfettamente identiche. Forse vi stupirà sapere che l’angolo dello scatto è identico in ambedue le coppie di foto. Ma allora perché ci sembrano ‘inclinate’ in modo diverso?
La colpa è del nostro sistema visivo: il nostro cervello, infatti, tende a interpretare le due immagini distinte come facenti parte di un insieme, di una scena unica, e quindi si fa “confondere” dalle regole della prospettiva. Questo tipo d’illusioni funziona con qualsiasi foto che coinvolge strutture i cui delineamenti si allontanano e convergono all'orizzonte - come torri, strade, binari ferroviari, ecc. Provate ad affiancare due immagini identiche, una accanto all’altra: le caratteristiche del paesaggio in una di loro appariranno sempre più inclinate rispetto all’altra.
Figura 2
La misura apparente delle cose che ci circondano, quando viene stimata senza l’aiuto di strumenti, è oggetto di illusioni visive che ingannano profondamente la percezione. Come accade molto spesso, le illusioni nella valutazione delle dimensioni degli oggetti nascono anche dal fatto che, tra un oggetto stampato su carta e quello reale, c’è collusione. Il nostro cervello interpreta le foto come degli oggetti tridimensionali e non come semplici rappresentazioni sul piano.
Tutto gira intorno alle ‘grandezze apparenti’... Ma che cos’è precisamente una grandezza apparente? Le linee che partono dalle estremità di un oggetto visto da una certa distanza e l’occhio formano un triangolo, il cui vertice situato dalla parte dell’occhio rappresenta appunto l’angolo visivo che determina la “grandezza angolare” o grandezza apparente dell’oggetto (vedi Query 30, L’illusione lunare).
Figura 3 
Figura 4 Le grandezze apparenti seguono queste elementari regole prospettiche:
a) dati due oggetti eguali nello spazio, quello di maggiori dimensioni angolari è percepito come più vicino;
b) dati due oggetti nello spazio di stessa grandezza angolare, quello che appare più distante è percepito come più grande.
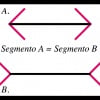
L’esempio della fig. 3, segue la regola b) che abbiamo appena citato. Benché le due penne a sfera siano esattamente della stessa lunghezza, quella che appare più lontana viene percepita automaticamente come più grande. È così che succede nella vita reale, ma su carta è diverso!
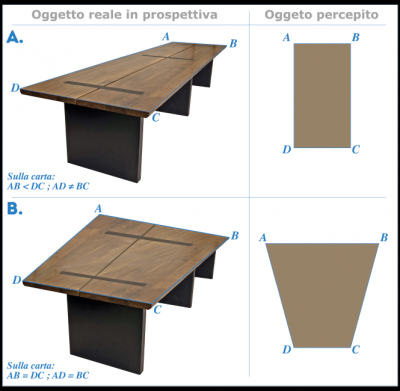
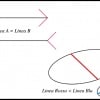
Per questi motivi, il piano del tavolo A qui accanto è percepito nella vita reale come un rettangolo (regola a), mentre il piano del tavolo B verrà percepito come un trapezio (regola b). Ora, sebbene i lati AB e DC di quest’ultimo siano uguali sulla carta, il lato AB sembrerà più lungo. Vero?
Se colleghiamo, due a due, dei punti identici di ciascuna coppia di foto, otterremo un parallelogramma ABCD. Nell’esempio in fig. 5, le linee seguono i contrafforti della cattedrale, allorché in fig. 6, le linee costeggiano il muretto. Ciononostante, l’effetto è lo stesso, il lato AB sembrerà più lungo del lato DC perché appare più lontano (regola b qui sopra), facendoci credere che le linee AD e BC divergano e creando la falsa impressione che le due immagini possiedano delle pendenze leggermente diverse.
Quod erat demonstrandum.
Figura 5 
Figura 6 Ma perché il cervello utilizza queste regole della prospettiva? Semplicemente per permetterci di percepire gli oggetti come immutati quando evolvono nello spazio.
Infine, approfittiamo di questo spazio per annunciarvi che il nostro prossimo libro “Illusioni Ottiche”, edito da Armenia (ISBN: 8834432290), uscirà il 23 giugno prossimo in tutte le librerie e sarà acquistabile su Amazon: goo.gl/HwCnUM .
Inoltre, abbiamo aperto un canale su Youtube (Dr. Archimedes) dove potrete seguire i nostri esperimenti sulla percezione visiva e i nostri tutorial: goo.gl/2cS7Pv .
Il Duomo di Firenze in fig. 1.a e la strada in fig. 2.b sembrano avere una maggiore pendenza della loro controparte, sebbene siano perfettamente identiche. Forse vi stupirà sapere che l’angolo dello scatto è identico in ambedue le coppie di foto. Ma allora perché ci sembrano ‘inclinate’ in modo diverso?
La colpa è del nostro sistema visivo: il nostro cervello, infatti, tende a interpretare le due immagini distinte come facenti parte di un insieme, di una scena unica, e quindi si fa “confondere” dalle regole della prospettiva. Questo tipo d’illusioni funziona con qualsiasi foto che coinvolge strutture i cui delineamenti si allontanano e convergono all'orizzonte - come torri, strade, binari ferroviari, ecc. Provate ad affiancare due immagini identiche, una accanto all’altra: le caratteristiche del paesaggio in una di loro appariranno sempre più inclinate rispetto all’altra.
Spiegazione tramite la geometria e la prospettiva
La misura apparente delle cose che ci circondano, quando viene stimata senza l’aiuto di strumenti, è oggetto di illusioni visive che ingannano profondamente la percezione. Come accade molto spesso, le illusioni nella valutazione delle dimensioni degli oggetti nascono anche dal fatto che, tra un oggetto stampato su carta e quello reale, c’è collusione. Il nostro cervello interpreta le foto come degli oggetti tridimensionali e non come semplici rappresentazioni sul piano.
Tutto gira intorno alle ‘grandezze apparenti’... Ma che cos’è precisamente una grandezza apparente? Le linee che partono dalle estremità di un oggetto visto da una certa distanza e l’occhio formano un triangolo, il cui vertice situato dalla parte dell’occhio rappresenta appunto l’angolo visivo che determina la “grandezza angolare” o grandezza apparente dell’oggetto (vedi Query 30, L’illusione lunare).
a) dati due oggetti eguali nello spazio, quello di maggiori dimensioni angolari è percepito come più vicino;
b) dati due oggetti nello spazio di stessa grandezza angolare, quello che appare più distante è percepito come più grande.
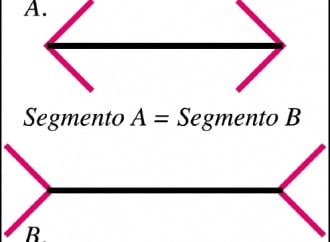
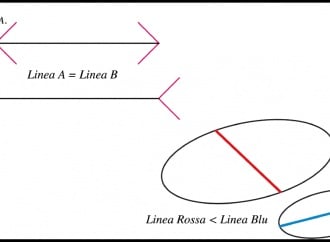
L’esempio della fig. 3, segue la regola b) che abbiamo appena citato. Benché le due penne a sfera siano esattamente della stessa lunghezza, quella che appare più lontana viene percepita automaticamente come più grande. È così che succede nella vita reale, ma su carta è diverso!
Per questi motivi, il piano del tavolo A qui accanto è percepito nella vita reale come un rettangolo (regola a), mentre il piano del tavolo B verrà percepito come un trapezio (regola b). Ora, sebbene i lati AB e DC di quest’ultimo siano uguali sulla carta, il lato AB sembrerà più lungo. Vero?
Se colleghiamo, due a due, dei punti identici di ciascuna coppia di foto, otterremo un parallelogramma ABCD. Nell’esempio in fig. 5, le linee seguono i contrafforti della cattedrale, allorché in fig. 6, le linee costeggiano il muretto. Ciononostante, l’effetto è lo stesso, il lato AB sembrerà più lungo del lato DC perché appare più lontano (regola b qui sopra), facendoci credere che le linee AD e BC divergano e creando la falsa impressione che le due immagini possiedano delle pendenze leggermente diverse.
Quod erat demonstrandum.
Infine, approfittiamo di questo spazio per annunciarvi che il nostro prossimo libro “Illusioni Ottiche”, edito da Armenia (ISBN: 8834432290), uscirà il 23 giugno prossimo in tutte le librerie e sarà acquistabile su Amazon: goo.gl/HwCnUM .
Inoltre, abbiamo aperto un canale su Youtube (Dr. Archimedes) dove potrete seguire i nostri esperimenti sulla percezione visiva e i nostri tutorial: goo.gl/2cS7Pv .
