Ricomporre un puzzle con pezzi triangolari può portare a conclusioni para-dossali. Infatti, il rompicapo di “sparizione geometrica” che presentiamo (vedi fig. 1a e 1b) possiede la caratteristica ‘magica’ di far svanire e riappa-rire a piacere uno spazio vuoto o una figura, secondo l’ordine nel quale ven-gono riuniti i 4 pezzi del gioco. Ovviamente si tratta di un’illusione, ma è dif-ficile non cascarci!
Nella fig. 1b si vede benissimo che, quando i 2 pezzi triangolari del puzzle vengono scambiati, un teschio ‘sbuca’ dal nulla. Ma come giustamente disse il chimico francese Lavoisier: «Nulla si crea, nulla si distrugge, tutto si tra-sforma»... Quindi, il guadagno (o la perdita) apparente di superficie deve es-sere per forza compensato da una perdita (o da un guadagno) in altre parti del puzzle. Ma dove e come?
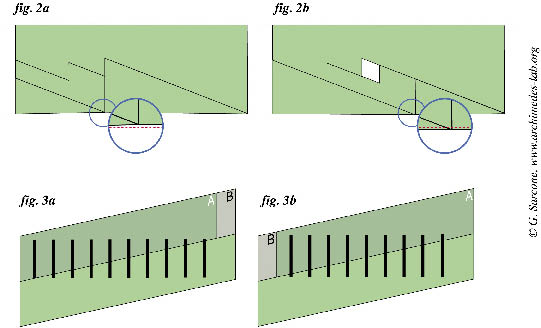
Per capire meglio il fenomeno di sparizione/apparizione del teschio prendia-mo come esempio il rompicapo di 3 pezzi in fig. 3a. Per semplificare, abbia-mo sostituito i teschi con una fila di linee verticali. Ora, permutando i pezzi A e B del puzzle sembrerà che una linea scompaia nel nulla (fig. 3b). In real-tà, porzioni della linea volatilizzata vengono semplicemente ridistribuite sulle 9 linee rimanenti. Infatti, se si misura accuratamente l’altezza delle linee ver-ticali prima e dopo, appare una piccola differenza nella lunghezza. Lo stesso discorso vale per i teschi. Coloro che vorrebbero eseguire questo gioco in classe o per un laboratorio di matemagia possono visitare la nostra pagina online: http://www.archimedes-lab.org/workshop13skulls.html dove troveranno tutte le informazioni relative alla sua realizzazione.
I puzzle creati dagli autori sono tratti dai libri “Fantastic Optical Illusions”, ISBN:184442295X, e “Drawing Optical Illu-sions”, ISBN:1848378203.
Nella fig. 1b si vede benissimo che, quando i 2 pezzi triangolari del puzzle vengono scambiati, un teschio ‘sbuca’ dal nulla. Ma come giustamente disse il chimico francese Lavoisier: «Nulla si crea, nulla si distrugge, tutto si tra-sforma»... Quindi, il guadagno (o la perdita) apparente di superficie deve es-sere per forza compensato da una perdita (o da un guadagno) in altre parti del puzzle. Ma dove e come?
Un ingegnoso inganno
Osservando bene la base del rettangolo composto dai 4 pezzi del gioco, è possibile notare che le rispettive basi dei triangoli non sono perfettamente collineari tra loro (ossia: giacenti su una stessa linea retta). Nella fig. 2a, il punto in cui i due triangoli si incontrano è leggermente rientrato, mentre in fig. 2b è sporgente. L’area della superficie ‘mancante’ (il buco) in fig. 2b è semplicemente ridistribuita all’interno di questa linea spezzata convessa.Per capire meglio il fenomeno di sparizione/apparizione del teschio prendia-mo come esempio il rompicapo di 3 pezzi in fig. 3a. Per semplificare, abbia-mo sostituito i teschi con una fila di linee verticali. Ora, permutando i pezzi A e B del puzzle sembrerà che una linea scompaia nel nulla (fig. 3b). In real-tà, porzioni della linea volatilizzata vengono semplicemente ridistribuite sulle 9 linee rimanenti. Infatti, se si misura accuratamente l’altezza delle linee ver-ticali prima e dopo, appare una piccola differenza nella lunghezza. Lo stesso discorso vale per i teschi. Coloro che vorrebbero eseguire questo gioco in classe o per un laboratorio di matemagia possono visitare la nostra pagina online: http://www.archimedes-lab.org/workshop13skulls.html dove troveranno tutte le informazioni relative alla sua realizzazione.
I puzzle creati dagli autori sono tratti dai libri “Fantastic Optical Illusions”, ISBN:184442295X, e “Drawing Optical Illu-sions”, ISBN:1848378203.