«Signore e signori, benvenuti. Assisterete nelle prossime righe a magie stupefacenti... queste pagine sono state incantate per portarvi nell’occulto mondo dell’ignoto...
Cominciamo canticchiando questa famosa ninna nanna:
Twinkle, twinkle, little star,
How I wonder what you are
Up above the world so high,
Like a diamond in the sky.
Twinkle, twinkle, little star
How I wonder what you are.
Scegli una qualunque parola nei primi due versi della poesia (ad esempio star), conta e ricorda il numero di lettere (in questo caso, quattro). Conta, a partire dalla parola successiva a quella selezionata (nell’esempio, how) un numero di parole pari al numero ricordato (in questo caso, conta quattro parole, arrivando a what). Ricomincia da dove sei arrivato, contando il numero di lettere della nuova parola e proseguendo allo stesso modo. Continua finché non riesci ad andare più avanti.
Su che parola sei finito? Te lo dico io: su you dell’ultimo verso! Incredibile, e abbiamo appena cominciato!
Come dici? Il trucco è nella ninna nanna? Non credi che funzioni anche con altri testi? Allora prova con questo articolo, cominciando da una parola nel primo paragrafo dopo la poesia. Sono certo che arriverai esattamente qui.
Continuiamo, ti invito ora a prendere un mazzo di carte francesi, so che c’è a casa tua! Va bene anche un mazzo di napoletane, piacentine... la magia che permea queste righe è potente, funzionerà allo stesso modo.
Non hai ancora il mazzo? Non proseguire, aspetto qui...
Bene, si parte. Mischia il mazzo, poi crea tre mazzetti coperti, ognuno di tre carte. Ci serviranno solo queste nove carte. Guarda la carta in fondo al primo mazzetto e ricordala...
Metti il primo mazzetto sul secondo, poi tutto sul terzo.
Bene, ora dì a voce alta il nome della carta che hai visto. Se hai paura che, nonostante io sia solo un pensiero scritto, possa sentirti, dì invece il nome di un’altra carta: - Kappa di Fiori! -, - Dieci di Bastoni! -, - Regina di Cuori! -.
Prendi il mazzo in mano e comincia a mettere le carte sul tavolo partendo dalla cima, una alla volta, formando una nuova pila a faccia in giù. Fai lo spelling della prima parola della carta che hai nominato (ad esempio, con Asso di Fiori, poggia sul tavolo la prima carta del mazzo dicendo A, poi la seconda sopra la prima dicendo S, poi ancora S, infine O). Quando finisci la prima parola prendi il mazzo rimasto e mettilo sopra quello sul tavolo. Riprendi tutto in mano e ripeti per le due parole successive (di Fiori nell’esempio): prima spelling, poi il resto sopra. Ci vuole molto meno a farlo dal vivo che a leggerlo.
Finito? Io non conosco la tua carta, tu potresti addirittura averne detta un’altra, eppure so che basta un po’ di magia... fai lo spelling di Magia e rivela la carta corrispondente all’ultima A... scommetto che la riconoscerai.»
Non c’è trucco, non c’è inganno... e in qualche senso è vero: in alcune esibizioni di magia la spiegazione non si cela dietro giochi di mano o abilità di prestidigitazione, piuttosto è un concetto sorprendente che si regge in piedi da sé, perché si può astrarre in un’idea matematica, a volte complicata, a volte semplicemente inaspettata. Non c’è niente di irrazionalmente magico, al contrario è la matematica a rendere il tutto razionalmente valido. In questi casi l’abilità del mago sta tutta nel deviare l’attenzione e creare l’atmosfera onirica dello spettacolo.
Partiamo da una variante del primo gioco: lo spettatore mischia un mazzo di carte e sceglie segretamente un numero da 1 a 10. Rivela lentamente le carte, una alla volta, a partire dalla cima del mazzo. Ad ogni carta rivelata riduce di uno il numero pensato, continuando fino a raggiungere zero. Guarda il numero della carta rivelata sullo zero e lo memorizza. Ricomincia il conto alla rovescia e continua così finché non può più andare avanti. L’ultima carta su cui ha contato zero sarà la carta bersaglio e il mago, naturalmente, la indovinerà dopo pochi istanti.
Questa modalità di contare le carte, o le parole nel primo caso, è detto Kruskal Count, e il funzionamento è dovuto al trucco matematico secondo il quale per la maggior parte delle volte, qualunque sia il numero segreto, si arriverà sempre alla stessa carta. Al mago quindi basterà ripetere le istruzioni impartite allo spettatore, cominciando dal numero segreto 1, per ottenere il suo stesso risultato. Il processo matematico coinvolto è piuttosto complesso e chiama in causa tanta teoria della probabilità (dettagli nell’articolo in bibliografia). È sì possibile che il trucco non riesca, ma la probabilità di fallimento diminuisce molto all’aumentare della lunghezza del conteggio, con più carte o più parole, come nel caso della ninna nanna.
Il principio matematico dietro il secondo gioco presentato è invece piuttosto elementare ed è basato sull’inversione dell’ordine delle carte. Per prima cosa, è importante notare la struttura del nome di una carta: Kappa di Fiori, Dieci di Bastoni, Regina di Cuori..., prima c’è sempre una parola di almeno 3 lettere (attenzione a Re, meglio che diventi King o Kappa), poi una di esattamente due, poi una di almeno cinque.
Il gioco è fatto! La parola Magia è di 5 lettere, quindi in corrispondenza dell’ultima A ci sarà sempre la carta cercata.
Ora, fra tutte le magie esistenti, mi sono concentrato su due esempi non solo basati su principi matematici, ma automatici, ovvero funzionanti senza l’intervento attivo del mago, e del tutto indipendenti dalle azioni del mago, così da poterli presentare in maniera efficace in un testo scritto. Le prossime magie si presenteranno in maniera diversa e il lettore non sarà affascinato dall’effetto in sé, quanto dalla sua spiegazione. L’invito in questo caso è proprio cercare di capire come funziona, più che rimanere stupiti.
Dato che abbiamo fatto cadere il velo, ora che è evidente l’argomento di questo articolo, ecco un gioco che non nasconde la sua origine matematica e mostra come alcuni principi si prestino piuttosto bene a essere utilizzati per stupire, meravigliare e confondere.
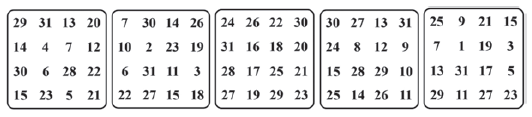
«Il mago chiede allo spettatore di pensare a un numero da 1 a 31 e poi gli mostra delle tessere, facendole scorrere davanti agli occhi una alla volta. - Ogni volta che vedi il tuo numero, dimmelo -. Dopo pochi istanti, il mago annuncia il numero pensato, senza errori!»
Saresti in grado? Ecco le tessere, e no, la soluzione non è ha imparato tutte le posizioni a memoria: vedi immagine.
In questo gioco si utilizza un’idea matematica piuttosto versatile in ambito magico, la numerazione in base due, o binaria. In breve, per indicare una quantità, solitamente utilizziamo numeri che possono essere composti da dieci cifre differenti, e consideriamo spesso sinonimi i concetti di numero e quantità. Il decimale è però solo una convenzione, tanto che con il binario è possibile indicare una quantità utilizzando solo due cifre, 0 e 1. Sia d’esempio il numero binario 111. L’uno più a destra conta per le unità, vale quindi 1. La cifra al centro conta per le duine (le decine del decimale) e vale 2. La terza cifra conta le duine di duine, o quattrine (come le decine di decine, o centinaia del decimale) e vale 4: il numero 111 in binario è quindi la quantità che in decimale indichiamo con 1+2+4, ossia 7.
I numeri nelle schede vanno da 1 a 31, e in binario possono essere scritti utilizzando al più 5 cifre, come 18, che è 10010, o 10, che è 01010: la prima cifra, contando da destra, vale 1, la seconda 2, poi 4, 8, 16.
Se prendiamo la prima scheda e rappresentiamo in binario i numeri presenti, ci accorgiamo di un fatto particolare:
Nella prima scheda del gioco sono presenti tutti e soli i numeri la cui cifra binaria più a destra, rappresentante le unità, è 1. Nella seconda scheda, la seconda cifra binaria, quella del 2, è sempre 1, e così via. Per il mago è immediato capire il numero: gli basterà sommare i numeri più piccoli di ogni scheda indicata dallo spettatore, strategicamente disposti sempre nella stessa posizione (seconda riga, seconda colonna) per ottenere il risultato. Un esempio? Immaginiamo che il numero scelto sia 19. Lo spettatore dirà che è nella prima scheda (quella dell’1), nella seconda (del 2) e nella quinta (del 16): sommando 1, 2, 16 si ottiene la risposta. E questo perché 19 è 10011 in base due.
L’ultimo gioco che voglio proporre è sicuramente il migliore. Presenterò la performance qui sotto, ma se volete apprezzarla davvero, vi consiglio di cercarla su internet prima di continuare (consiglio il video Beautiful Card Trick – Numberphile su Youtube; oltre la performance c’è anche la spiegazione, ma quella potete leggerla qui sotto). Il gioco rientra nella categoria degli ACAAN (any card at any number), in cui una carta scelta dallo spettatore viene ritrovata in una data posizione all’interno del mazzo.
«Lo spettatore sceglie 27 carte da un mazzo e ne ricorda una, le altre non servono. Mischia e consegna il mazzo al mago. Il mago chiede - Qual è il tuo numero preferito tra 1 e 27? - mentre distribuisce le carte in tre mazzetti, a faccia in alto, una carta alla volta. Fatto ciò, lo spettatore indica in quale dei tre mazzetti si trova la sua carta.
Il mago prende le carte riformando il mazzo e ripete l’operazione due volte, ogni volta chiedendo allo spettatore la posizione nei tre mazzi della sua carta.
Alla fine, il mago conta un numero di carte dalla cima del mazzo pari al numero scelto dallo spettatore. La carta successiva sarà proprio la carta scelta!»
Come nel gioco precedente, anche qui l’idea è quella di sfruttare una base non decimale, in questo caso la base tre, per spostare un dato numero di carte sopra la carta bersaglio. Studiando il particolare modo in cui le 27 carte vengono mischiate è possibile ricostruire e modificare la posizione in cui finirà il bersaglio. In realtà non è una vera mescolata, dato che le carte vanno sempre ridistribuite con lo stesso ordine: prima il mazzetto a sinistra, poi quello al centro, poi quello a destra, poi di nuovo a sinistra e così via...
Per prima cosa, va scomposto il numero indicato dallo spettatore in base 3, ad esempio 19 diventa il ternario 201 (il primo 2 sta per le novine, lo zero per le terzine, l’1 per le unità)
Con il numero ternario appena calcolato, e cominciando da destra, ossia dalle unità, si assegna una posizione del mazzo ad ogni cifra:
ottenendo una combinazione come mezzo-cima-fondo (nel caso di 201). Tutto questo andrebbe calcolato a mente, mentre lo spettatore mischia, senza mostrarsi troppo concentrati.
Ogni volta che si rimonta il mazzo, bisogna avere la premura di far finire il mazzetto con la carta bersaglio in corrispondenza della combinazione ottenuta: con mezzo-cima-fondo ad esempio
Automaticamente il mazzo sarà pronto per la rivelazione finale.
Nota bene: con questo articolo non ho assolutamente portato avanti la tesi che, davanti ad un gioco di magia, si debba tentare in tutti i modi di scovare il trucco per avere qualche soddisfazione, siamo nel terzo millennio, dovrebbe essere evidente a tutti che il trucco c’è, non è quello il punto. La bellezza di un gioco è soprattutto nell’esperienza durante l’esecuzione, e si può provare solo una volta. Quando il cuore del gioco è basato sulla matematica, spesso poi si può provare un diverso stupore, quello di aver compreso il funzionamento, una sensazione diversa, più intellettuale. In questo senso si può dire che con questi giochi la soluzione è addirittura più interessante dell’esecuzione stessa.
Cominciamo canticchiando questa famosa ninna nanna:
Twinkle, twinkle, little star,
How I wonder what you are
Up above the world so high,
Like a diamond in the sky.
Twinkle, twinkle, little star
How I wonder what you are.
Scegli una qualunque parola nei primi due versi della poesia (ad esempio star), conta e ricorda il numero di lettere (in questo caso, quattro). Conta, a partire dalla parola successiva a quella selezionata (nell’esempio, how) un numero di parole pari al numero ricordato (in questo caso, conta quattro parole, arrivando a what). Ricomincia da dove sei arrivato, contando il numero di lettere della nuova parola e proseguendo allo stesso modo. Continua finché non riesci ad andare più avanti.
Su che parola sei finito? Te lo dico io: su you dell’ultimo verso! Incredibile, e abbiamo appena cominciato!
Come dici? Il trucco è nella ninna nanna? Non credi che funzioni anche con altri testi? Allora prova con questo articolo, cominciando da una parola nel primo paragrafo dopo la poesia. Sono certo che arriverai esattamente qui.
Continuiamo, ti invito ora a prendere un mazzo di carte francesi, so che c’è a casa tua! Va bene anche un mazzo di napoletane, piacentine... la magia che permea queste righe è potente, funzionerà allo stesso modo.
Non hai ancora il mazzo? Non proseguire, aspetto qui...
Bene, si parte. Mischia il mazzo, poi crea tre mazzetti coperti, ognuno di tre carte. Ci serviranno solo queste nove carte. Guarda la carta in fondo al primo mazzetto e ricordala...
Metti il primo mazzetto sul secondo, poi tutto sul terzo.
Bene, ora dì a voce alta il nome della carta che hai visto. Se hai paura che, nonostante io sia solo un pensiero scritto, possa sentirti, dì invece il nome di un’altra carta: - Kappa di Fiori! -, - Dieci di Bastoni! -, - Regina di Cuori! -.
Prendi il mazzo in mano e comincia a mettere le carte sul tavolo partendo dalla cima, una alla volta, formando una nuova pila a faccia in giù. Fai lo spelling della prima parola della carta che hai nominato (ad esempio, con Asso di Fiori, poggia sul tavolo la prima carta del mazzo dicendo A, poi la seconda sopra la prima dicendo S, poi ancora S, infine O). Quando finisci la prima parola prendi il mazzo rimasto e mettilo sopra quello sul tavolo. Riprendi tutto in mano e ripeti per le due parole successive (di Fiori nell’esempio): prima spelling, poi il resto sopra. Ci vuole molto meno a farlo dal vivo che a leggerlo.
Finito? Io non conosco la tua carta, tu potresti addirittura averne detta un’altra, eppure so che basta un po’ di magia... fai lo spelling di Magia e rivela la carta corrispondente all’ultima A... scommetto che la riconoscerai.»
Non c’è trucco, non c’è inganno... e in qualche senso è vero: in alcune esibizioni di magia la spiegazione non si cela dietro giochi di mano o abilità di prestidigitazione, piuttosto è un concetto sorprendente che si regge in piedi da sé, perché si può astrarre in un’idea matematica, a volte complicata, a volte semplicemente inaspettata. Non c’è niente di irrazionalmente magico, al contrario è la matematica a rendere il tutto razionalmente valido. In questi casi l’abilità del mago sta tutta nel deviare l’attenzione e creare l’atmosfera onirica dello spettacolo.
Partiamo da una variante del primo gioco: lo spettatore mischia un mazzo di carte e sceglie segretamente un numero da 1 a 10. Rivela lentamente le carte, una alla volta, a partire dalla cima del mazzo. Ad ogni carta rivelata riduce di uno il numero pensato, continuando fino a raggiungere zero. Guarda il numero della carta rivelata sullo zero e lo memorizza. Ricomincia il conto alla rovescia e continua così finché non può più andare avanti. L’ultima carta su cui ha contato zero sarà la carta bersaglio e il mago, naturalmente, la indovinerà dopo pochi istanti.
Questa modalità di contare le carte, o le parole nel primo caso, è detto Kruskal Count, e il funzionamento è dovuto al trucco matematico secondo il quale per la maggior parte delle volte, qualunque sia il numero segreto, si arriverà sempre alla stessa carta. Al mago quindi basterà ripetere le istruzioni impartite allo spettatore, cominciando dal numero segreto 1, per ottenere il suo stesso risultato. Il processo matematico coinvolto è piuttosto complesso e chiama in causa tanta teoria della probabilità (dettagli nell’articolo in bibliografia). È sì possibile che il trucco non riesca, ma la probabilità di fallimento diminuisce molto all’aumentare della lunghezza del conteggio, con più carte o più parole, come nel caso della ninna nanna.
Il principio matematico dietro il secondo gioco presentato è invece piuttosto elementare ed è basato sull’inversione dell’ordine delle carte. Per prima cosa, è importante notare la struttura del nome di una carta: Kappa di Fiori, Dieci di Bastoni, Regina di Cuori..., prima c’è sempre una parola di almeno 3 lettere (attenzione a Re, meglio che diventi King o Kappa), poi una di esattamente due, poi una di almeno cinque.
- Inizialmente, per come è stato riformato il mazzetto, la carta bersaglio, ad esempio il Sette di Denari, si troverà in 3° posizione contando dall’alto. Facendo lo spelling, l’ordine delle carte si inverte;
- con la prima parola, Sette, si inverte l’ordine di almeno tre carte, poi si mette il resto sopra le carte appena posate. La carta bersaglio sarà stata sicuramente mossa, e finirà in 7° posizione;
- con la seconda parola, Di, si invertono due carte, poi si mette il resto del mazzo sopra. Stavolta la carta bersaglio non sarà stata sicuramente mossa, e si ritroverà in 5° posizione, avendo tolto due carte dalla cima.
- con lo stesso ragionamento, con la terza parola, Denari, si invertono almeno cinque carte, compreso il bersaglio, che si troverà sempre in 5° posizione.
Il gioco è fatto! La parola Magia è di 5 lettere, quindi in corrispondenza dell’ultima A ci sarà sempre la carta cercata.
Ora, fra tutte le magie esistenti, mi sono concentrato su due esempi non solo basati su principi matematici, ma automatici, ovvero funzionanti senza l’intervento attivo del mago, e del tutto indipendenti dalle azioni del mago, così da poterli presentare in maniera efficace in un testo scritto. Le prossime magie si presenteranno in maniera diversa e il lettore non sarà affascinato dall’effetto in sé, quanto dalla sua spiegazione. L’invito in questo caso è proprio cercare di capire come funziona, più che rimanere stupiti.
Dato che abbiamo fatto cadere il velo, ora che è evidente l’argomento di questo articolo, ecco un gioco che non nasconde la sua origine matematica e mostra come alcuni principi si prestino piuttosto bene a essere utilizzati per stupire, meravigliare e confondere.
«Il mago chiede allo spettatore di pensare a un numero da 1 a 31 e poi gli mostra delle tessere, facendole scorrere davanti agli occhi una alla volta. - Ogni volta che vedi il tuo numero, dimmelo -. Dopo pochi istanti, il mago annuncia il numero pensato, senza errori!»
Saresti in grado? Ecco le tessere, e no, la soluzione non è ha imparato tutte le posizioni a memoria: vedi immagine.
In questo gioco si utilizza un’idea matematica piuttosto versatile in ambito magico, la numerazione in base due, o binaria. In breve, per indicare una quantità, solitamente utilizziamo numeri che possono essere composti da dieci cifre differenti, e consideriamo spesso sinonimi i concetti di numero e quantità. Il decimale è però solo una convenzione, tanto che con il binario è possibile indicare una quantità utilizzando solo due cifre, 0 e 1. Sia d’esempio il numero binario 111. L’uno più a destra conta per le unità, vale quindi 1. La cifra al centro conta per le duine (le decine del decimale) e vale 2. La terza cifra conta le duine di duine, o quattrine (come le decine di decine, o centinaia del decimale) e vale 4: il numero 111 in binario è quindi la quantità che in decimale indichiamo con 1+2+4, ossia 7.
I numeri nelle schede vanno da 1 a 31, e in binario possono essere scritti utilizzando al più 5 cifre, come 18, che è 10010, o 10, che è 01010: la prima cifra, contando da destra, vale 1, la seconda 2, poi 4, 8, 16.
Se prendiamo la prima scheda e rappresentiamo in binario i numeri presenti, ci accorgiamo di un fatto particolare:
Nella prima scheda del gioco sono presenti tutti e soli i numeri la cui cifra binaria più a destra, rappresentante le unità, è 1. Nella seconda scheda, la seconda cifra binaria, quella del 2, è sempre 1, e così via. Per il mago è immediato capire il numero: gli basterà sommare i numeri più piccoli di ogni scheda indicata dallo spettatore, strategicamente disposti sempre nella stessa posizione (seconda riga, seconda colonna) per ottenere il risultato. Un esempio? Immaginiamo che il numero scelto sia 19. Lo spettatore dirà che è nella prima scheda (quella dell’1), nella seconda (del 2) e nella quinta (del 16): sommando 1, 2, 16 si ottiene la risposta. E questo perché 19 è 10011 in base due.
L’ultimo gioco che voglio proporre è sicuramente il migliore. Presenterò la performance qui sotto, ma se volete apprezzarla davvero, vi consiglio di cercarla su internet prima di continuare (consiglio il video Beautiful Card Trick – Numberphile su Youtube; oltre la performance c’è anche la spiegazione, ma quella potete leggerla qui sotto). Il gioco rientra nella categoria degli ACAAN (any card at any number), in cui una carta scelta dallo spettatore viene ritrovata in una data posizione all’interno del mazzo.
«Lo spettatore sceglie 27 carte da un mazzo e ne ricorda una, le altre non servono. Mischia e consegna il mazzo al mago. Il mago chiede - Qual è il tuo numero preferito tra 1 e 27? - mentre distribuisce le carte in tre mazzetti, a faccia in alto, una carta alla volta. Fatto ciò, lo spettatore indica in quale dei tre mazzetti si trova la sua carta.
Il mago prende le carte riformando il mazzo e ripete l’operazione due volte, ogni volta chiedendo allo spettatore la posizione nei tre mazzi della sua carta.
Alla fine, il mago conta un numero di carte dalla cima del mazzo pari al numero scelto dallo spettatore. La carta successiva sarà proprio la carta scelta!»
Come nel gioco precedente, anche qui l’idea è quella di sfruttare una base non decimale, in questo caso la base tre, per spostare un dato numero di carte sopra la carta bersaglio. Studiando il particolare modo in cui le 27 carte vengono mischiate è possibile ricostruire e modificare la posizione in cui finirà il bersaglio. In realtà non è una vera mescolata, dato che le carte vanno sempre ridistribuite con lo stesso ordine: prima il mazzetto a sinistra, poi quello al centro, poi quello a destra, poi di nuovo a sinistra e così via...
Per prima cosa, va scomposto il numero indicato dallo spettatore in base 3, ad esempio 19 diventa il ternario 201 (il primo 2 sta per le novine, lo zero per le terzine, l’1 per le unità)
Con il numero ternario appena calcolato, e cominciando da destra, ossia dalle unità, si assegna una posizione del mazzo ad ogni cifra:
- 0: cima;
- 1: mezzo;
- 2: fondo;
ottenendo una combinazione come mezzo-cima-fondo (nel caso di 201). Tutto questo andrebbe calcolato a mente, mentre lo spettatore mischia, senza mostrarsi troppo concentrati.
Ogni volta che si rimonta il mazzo, bisogna avere la premura di far finire il mazzetto con la carta bersaglio in corrispondenza della combinazione ottenuta: con mezzo-cima-fondo ad esempio
- deve finire in mezzo dopo la prima mescolata;
- in cima dopo la seconda;
- in fondo dopo la terza.
Automaticamente il mazzo sarà pronto per la rivelazione finale.
Riferimenti bibliografici
- The Kruskal Count – Jeffrey C. Lagarias, Eric Rains, Robert J. Vanderbei, su arXiv
- Beautiful Card Trick - Numberphile su Youtube
- The Number Illusion You Won’t Believe – Vsauce2 su Youtube
- Magic Spelling – D!NG su Youtube
- Come indovinare l’età di qualsiasi persona – Hyde su YoutubE
Nota bene: con questo articolo non ho assolutamente portato avanti la tesi che, davanti ad un gioco di magia, si debba tentare in tutti i modi di scovare il trucco per avere qualche soddisfazione, siamo nel terzo millennio, dovrebbe essere evidente a tutti che il trucco c’è, non è quello il punto. La bellezza di un gioco è soprattutto nell’esperienza durante l’esecuzione, e si può provare solo una volta. Quando il cuore del gioco è basato sulla matematica, spesso poi si può provare un diverso stupore, quello di aver compreso il funzionamento, una sensazione diversa, più intellettuale. In questo senso si può dire che con questi giochi la soluzione è addirittura più interessante dell’esecuzione stessa.