Chi ritiene che non tutti i cerchi nel grano siano fatti con attrezzi semplici come corde e assi sostiene quest'idea citando svariate presunte anomalie che sarebbero rintracciabili nei cerchi genuini (qualunque cosa significhi questo termine). Tra queste, l'allungamento dei nodi degli steli si distingue non solo per essere una delle più citate in assoluto, ma anche perché, stando all'ingegnere olandese Eltjo H. Haselhoff, da uno studio matematico del suo andamento sarebbe possibile dedurne l'origine: una radiazione emessa da una non meglio identificata sfera di luce (BOL, da Ball Of Light).

Nodi e allungamenti

I nodi sono piccole sezioni dello stelo con caratteristiche particolari e hanno l'aspetto di anelli di colore diverso dal resto dello stelo. Normalmente sono lunghi qualche millimetro (due-quattro). Una delle loro funzioni è di consentire allo stelo di piegarsi, il che è utile in varie situazioni: la pianta può protendersi verso la luce e può rialzarsi almeno in parte dopo uno schiacciamento al suolo. In casi del genere sono proprio i nodi, deformandosi, a inclinare lo stelo nella direzione voluta. La deformazione avviene per allungamento selettivo di un lato del nodo. Esiste nella pianta un sistema di controllo ormonale che pilota l'allungamento dei nodi e che è sensibile alla luce (fototropismo) e alla gravità (gravitropismo o geotropismo); entrambi i tropismi possono attivarsi nel caso di una pianta schiacciata.

Alcuni studiosi del fenomeno crop circle hanno notato da tempo che in almeno una parte dei cerchi i nodi appaiono notevolmente allungati. Nonostante questo fatto venga spesso citato come un'anomalia, di per sé non appare molto strano, dato che i nodi sono fatti apposta per allungarsi e risultano molto allungati anche nelle piante appiattite al suolo da vento, pioggia e intemperie varie. Di fronte a questo fatto, qualcuno, come Nancy Talbott del gruppo BLT (Burke, Levengood & Talbott), uno dei principali gruppi di ricerca sui cerchi nel grano, arriva a sostenere che le zone irregolari di piante piegate, che contadini e agronomi attribuiscono appunto alle intemperie o a un eccesso di fertilizzazione, non siano affatto prodotte da queste cause ma dallo stesso fenomeno che produce gli schiacciamenti geometrici, cioè i cerchi nel grano propriamente detti. Quest'idea porta a svariati problemi concettuali e metodologici, tra i quali spicca il rischio di circolarità del ragionamento: un cerchio è genuino perché i nodi sono allungati, l'allungamento è un'anomalia perché capita solo nei cerchi genuini... la tesi di base che l'allungamento dei nodi sia un'anomalia deve essere dimostrata in qualche altro modo.

Nel 1994 Levengood pubblicò un articolo sulla rivista scientifica Physiologia Plantarum^[1]in cui parlava di svariate anomalie che sarebbero state trovate nei cerchi nel grano; tra queste figurava naturalmente l'allungamento dei nodi.

Più interessante, ai fini della presente analisi, è il successivo articolo del 1999 firmato da Levengood e Talbott ^[2], interamente dedicato a questa presunta anomalia. In quest'articolo veniva presentato il risultato di un esperimento di piegatura del grano con corde e assi, dove sarebbe stato osservato un progressivo allungamento dei nodi dopo la piegatura, dell'ordine del 2% al giorno. Dopo un'intera settimana l'allungamento era ancora inferiore al 20%, mentre in cerchi ritenuti genuini gli autori dichiaravano di aver misurato allungamenti tra il 30% e il 200% dopo soli tre giorni dalla formazione. È questa la tanto sospirata prova che l'anomalia è anomala? Lo vedremo più avanti. Nell'articolo Levengood e Talbott citavano tre cerchi nel grano (Devizes 1993, Chehalis 1994 e Sussex 1994) dove l'allungamento dei nodi appariva dipendente dalla distanza dal centro della formazione: nodi più lunghi al centro, meno lunghi ai bordi. Veniva anche proposto un modello matematico di vortice di plasma per tentare di spiegare questa dipendenza dalla distanza. L'idea era che un ipotetico vortice al centro del cerchio, oltre a piegare le piante con lo spostamento d'aria, irradiasse onde elettromagnetiche e fossero queste a provocare l'allungamento dei nodi per dilatazione termica. A questo proposito è forse opportuno sfatare un mito piuttosto diffuso: Levengood non ha mai scritto in alcuno di questi articoli di aver riprodotto l'allungamento dei nodi mettendo delle spighe in un forno a microonde. Ha dichiarato invece di aver riprodotto in questo modo la dilatazione dei pori delle pareti cellulari (cell wall pits), strutture microscopiche che non hanno niente a che fare con i nodi. Se avesse riprodotto anche l'allungamento dei nodi, perché avrebbe omesso dall'articolo un dettaglio così cruciale? Tra chi si interessa di cerchi nel grano è anche piuttosto diffuso un equivoco: in alcune fotografie di steli prelevati da un crop circle si vedono nodi non solo allungati, ma anche piegati, quindi c'è chi pensa che qualche misterioso fenomeno agisca sui nodi, allungandoli e piegandoli, proprio allo scopo di creare il cerchio. Quelle fotografie ritraggono invece i nodi più allungati, che, stando ai dati di Levengood, sono gli ultimi (quelli più in alto lungo la spiga) o i penultimi, comunque non quelli in basso, dove la pianta è stata piegata per formare il cerchio. I tropismi attuati dalla pianta dopo uno schiacciamento al suolo provocano spesso la piegatura dei nodi lontani dalla base; si chiama ginocchiatura. Nel 2001 Haselhoff scrisse un commento all'ultimo articolo di Levengood e Talbott ^[3], pubblicato nella stessa rivista, dove criticava (giustamente) la loro analisi, mettendo in luce un paio di vistosi errori, e proponeva il proprio modello: non un vortice di plasma ma una sorgente puntiforme o sferica di radiazione (fig. 1).

In base a questo modello, l'allungamento dei nodi dovrebbe essere inversamente proporzionale al quadrato della distanza r; dovrebbe quindi essere massimo al di sotto della BOL e diminuire con la distanza, seguendo un andamento a campana. Haselhoff rianalizzò i dati delle tre formazioni pubblicati nell'articolo del 1999, reinterpretandoli alla luce del suo modello. Li confrontò poi con quelli da lui raccolti nel cerchio di Nieuwerkerk (o "di Dreischor"), di origine dichiaratamente umana, dove non trovò lo stesso andamento matematico.

Questi (criticabili) articoli e commenti sono stati tutti pubblicati su una rivista scientifica con referee, caso rarissimo nel campo degli studi sui cerchi nel grano. L'allungamento dei nodi è quindi, tra tutte le anomalie, quella con la più alta pretesa di scientificità; può quindi essere considerato appropriato criticare quegli articoli dalle pagine di una rivista scientifica ed è appunto ciò che è stato fatto poco tempo fa da Francesco Grassi, Claudio Cocheo e il sottoscritto ^[4]. Per questa ragione, nel seguito non tratterò di quei tre articoli, già analizzati in altra sede, ma degli ulteriori scritti di Haselhoff, non pubblicati su rivista scientifica.

Il cerchio di Hoeven (o di Noord-Badant)

Haselhoff scrive ^[5],^[6] che un giovane olandese asserì di aver visto, verso l'una e mezza di notte del 7 giugno 1999, una lucina di colore rosa chiaro muoversi nell'aria, poi trasformarsi in una forma ellittica e svanire lentamente, lasciandosi dietro un cerchio nel grano di circa nove metri di diametro, ancora caldo (letteralmente). La mattina dopo il giovane avrebbe visto anche un secondo cerchio di una sessantina di centimetri di diametro vicino al primo. Cinque notti dopo il testimone avrebbe visto un lampo di luce azzurro pallido provenire da un singolo punto; questa volta il testimone avrebbe trovato un altro cerchio di nove metri di diametro, ancora caldo. Il giorno dopo Haselhoff prelevò sul posto 25 campioni di piante da ognuno dei cerchi maggiori, due dal cerchio piccolo e nove lontani dai cerchi come gruppo di controllo. Ogni campione era costituito da una ventina di steli vicini tra loro. I campioni all'interno dei cerchi grandi furono raccolti seguendo uno schema a stella; quella del cerchio più vecchio è composta dalle "tracce" (insiemi di campioni raccolti in linea retta) A, B e C, l'altra dalle tracce D, E ed F (fig. 2). Le tracce A, B e C hanno in comune il campione centrale (A4=B4=C4) e così anche le D, E ed F.

Dopo aver lasciato seccare i campioni per alcuni mesi, Haselhoff misurò i nodi, calcolò gli allungamenti rispetto ai campioni di controllo, ne confrontò l'andamento con quello previsto dal suo modello a sfera di radiazione e giudicò che ci fosse una corrispondenza significativa. Nel suo libro La natura complessa dei cerchi nel grano5 Haselhoff presenta i dati relativi alla lunghezza dei nodi delle tracce A, B e C sotto forma di colorati grafici a barre (pp. 84-85). Riporto i dati in fig. 3 in una forma simile (omettendo per semplicità le deviazioni standard, non usate nell'analisi).

Nel libro non è invece riportato alcun grafico delle tracce D, E ed F; il loro andamento viene lasciato all'immaginazione del lettore. Haselhoff riporta il risultato di un'analisi statistica dei dati della sola traccia B alla luce del modello BOL (p. 88): il massimo grado di coincidenza tra il modello e i dati si ha ipotizzando una BOL ad un'altezza di 4,1 metri. Il coefficiente di Pearson risultante (di cosa si tratti sarà più chiaro nel seguito) è 0,988, un valore cioè molto prossimo all'unità che si otterrebbe se la corrispondenza fosse perfetta. Haselhoff scrive anche di aver eseguito la stessa analisi sui dati di un crop circle di sicura origine umana (Dreischor, 1997); non riporta il coefficiente così ottenuto, ma dichiara che era "del tutto insoddisfacente" (p. 89).

Haselhoff non azzarda alcuna ipotesi su come una BOL possa piegare le piante; di certo non asserisce che sia la radiazione della BOL a farlo, sarebbe alquanto implausibile sul piano fisico. Non precisa neanche di che natura sia questa radiazione; ipotizza che possa essere un misto di infrarossi o microonde e radiazioni ionizzanti, queste ultime per giustificare altre presunte anomalie (p. 130).

L'indagine ha inizio

Sul cerchio di Hoeven e sull'analisi condotta da Haselhoff è stato possibile reperire le seguenti fonti:

• il libro di Haselhoff precedentemente citato5. Pubblicato in più lingue e in più edizioni, ampiamente pubblicizzato nel sito del Dutch Center for Crop Circle Research (www.dcccs.org), notissimo agli appassionati, può certamente essere definito il magnum opus del ricercatore olandese;
• svariati articoli on-line ^[7] scritti da Haselhoff che si limitano a riportare le conclusioni del ricercatore, ma poco o nulla dei dati e dei calcoli su cui sarebbero basate;
  • un rapporto disponibile on-line7 nel sito del DCCCS che descrive abbastanza in dettaglio l'analisi che Haselhoff ha condotto sul crop circle di Hoeven. Ne esistono almeno due versioni che differiscono solo per l'impaginazione e l'intestazione: una sembra una comunicazione privata a Levengood, l'altra ha un'intestazione più generica e sembrerebbe un vero e proprio articolo. A prescindere dalla versione, questo testo è la fonte più completa e accurata tra tutte quelle che è stato possibile trovare sul crop circle di Hoeven ed è alla base della presente analisi.
  
  
  

  Procurarsi i dati

  
  Anche nel rapporto, purtroppo, i dati non sono presentati in forma numerica ed è stato quindi necessario rileggerli dai grafici a barre. Naturalmente, anche a causa del formato JPEG delle immagini (un GIF sarebbe stato più nitido), la procedura può aver introdotto qualche piccolo errore dell'ordine del pixel, ma... questa è la forma in cui Haselhoff ha pubblicato i suoi dati e questo è ciò che chiunque ha a disposizione per verificare le sue conclusioni. Ho scritto a Haselhoff chiedendogli i dati originali, ma non mi ha mai risposto. Riporto in tab.1 i valori ottenuti.
  
  

  Tabella 1. Lunghezza dei nodi in millimetri. "Co" = controlli. L'ultima cifra non è significativa ma è stata inclusa comunque nella tabella per uno scrupolo di perfetta riproducibilitá dell'analisi. A4, B4 e C4, che dovrebbero coincidere, danno un'idea dell'errore introdotto nella rilettura dei grafici. E4 ed F4 sono semplici copie di D4.
  
  Già ad una prima occhiata risulta evidente che le tracce D, E ed F (fig. 4), presenti nel rapporto ma omesse dal libro, hanno un aspetto del tutto diverso dalle A, B e C.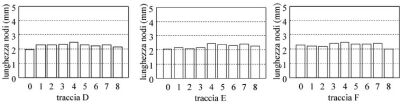
  
  

  Figura 4. Nel grafico originale i campioni di F sono numerati 0,7,6,5,(4),3,2,1,8, non si sa perché. Ho assunto che l'ordine spaziale fosse quello del grafico e ho rinumerato i campioni da 0 a 8.
  
  In queste tracce i nodi sono poco più lunghi di quelli di controllo (che sono mediamente di 2,054 mm) e non si vede traccia dell'andamento a campana che sarebbe tipico di una BOL, tant'è vero che i coefficienti di Pearson di queste tracce non sono neppure menzionati nel rapporto. Del cerchio di Dreischor avevo invece i dati originali, fornitimi da Francesco Grassi, che li aveva avuti tempo prima da Haselhoff.
  
  

  Metodo di analisi

  
  Ottenuti i dati, il passo successivo è verificare i calcoli.
  
  Per giudicare quanto un modello matematico si adatti ai dati reali bisogna calcolare i valori predetti dal modello e confrontarli con quelli reali, calcolando un unico numero che riassuma tutte le differenze riscontrate: si chiama "scarto quadratico medio" e lo indicherò con S. Minore è S, migliore è il modello. Spesso al posto di S si preferisce calcolare il "coefficiente di regressione" (o "di Pearson") R, che fornisce un valore compreso tra -1 e 1 e risulta di più facile interpretazione: 1 significa che c'è una perfetta correlazione tra i due insiemi di dati, 0 significa che non c'è alcuna correlazione lineare, -1 significa che la correlazione è negativa (il modello sembra sbagliato ad arte). Spesso si usa il quadrato di R, indicato come R². Nei suoi lavori Haselhoff usa appunto R o R². Il coefficiente di Pearson consente di confrontare modelli usando dati differenti, ma ha anche i suoi svantaggi: non sempre un R (o R²) maggiore implica un minor S, cioè una migliore corrispondenza tra il modello e i dati. Quando si confrontano modelli diversi con gli stessi dati (nel nostro caso, quelli dello stesso crop circle) è meglio guardare S. Il modello proposto da Haselhoff è questo:
  
  y = k / r² = k / (d² + h²)
  
  ossia, l'allungamento dei nodi (y) è assunto proporzionale a svariati fattori (energia totale emessa, grado di assorbimento da parte del tessuto vegetale...) tutti riassunti in un unico parametro k, e inversamente proporzionale al quadrato della distanza r (questa sarebbe la "firma" di una sorgente sferica di radiazione). A sua volta, la distanza r tra la BOL e la pianta, in base al teorema di Pitagora, può essere ottenuta dalla distanza d della pianta dal centro del cerchio e dall'altezza h della BOL, che si suppone fluttui sopra il centro del cerchio (fig. 1). Il problema è che non conosciamo né h né k. Ciò che ha fatto Haselhoff è stato di calcolare quali valori di h e k avrebbe dovuto avere una BOL per produrre gli effetti osservati, o, più esattamente, per produrre gli effetti più simili a quelli osservati (S minore nel confronto con i dati). Questa procedura, chiamata fitting, è ampiamente usata nella scienza e del tutto legittima; tuttavia è bene ricordare che più parametri liberi ha un modello, più è facile adattarlo a un insieme di dati qualunque e, di conseguenza, meno significativo è il risultato da un punto di vista statistico. Bisogna quindi essere cauti nel valutare i risultati.
  
  Ma come si calcolano questi h e k² Se il modello è semplice si può farlo per via analitica, cioè lavorando con carta e penna per dedurre dal modello una formula per calcolarli; è il metodo migliore, perché fornisce la soluzione esatta. Se il modello è più complesso si può procedere per via numerica, facendo cercare ad un computer i valori di h e k migliori, per tentativi (tanti). Infine si può andare per tentativi a mano, con carta e penna, che è il sistema più scomodo e impreciso. Nel caso del modello BOL ho ricavato analiticamente k da h e poi ho cercato il solo h con un computer.
  
  Una volta trovati i valori ottimali di h e k, è immediato calcolare S o R; ma dopo? Non è tanto facile capire quanto sia significativo, in assoluto, un certo valore di S o di R; se per esempio R=0,9, questo autorizza a dire che i dati comprovano l'ipotesi? O, meglio, che la dimostrano? Per avere un termine di paragone ho confrontato il modello di Haselhoff con il più semplice possibile modello a due parametri:
  
  y = ad + b
  
  ossia, una banalissima linea retta. Mi pare ragionevole pretendere che il modello di Haselhoff si adatti ai dati meglio di una retta, altrimenti non vedo proprio su quali basi si possa sostenere che i dati forniscono un'evidenza empirica a sostegno di quel modello. Il confronto con la retta ha in sostanza lo scopo di rispondere a una domanda: la curva prevista dal modello è obiettivamente deducibile dai dati, o è solo nell'occhio di chi giudica? Attenzione che non sto neppure pretendendo che il modello della BOL sia il migliore tra tutti quelli a due parametri; come test preliminare, mi accontento che sia migliore del più semplice.
  
  

  Elaborazione dei dati

  
  Sono disponibili 50 campioni, 25 per cerchio. Dato che le ipotetiche BOL responsabili dei due cerchi avrebbero potuto avere parametri h e k diversi, bisognerebbe analizzare separatamente i due insiemi di 25 campioni, calcolando per ogni cerchio i valori ottimali di h e k e i risultanti S ed R. Il metodo seguito da Haselhoff appare invece affetto da tre gravi errori:
  
  1) Per prima cosa, i 25 campioni del secondo cerchio vengono ignorati; nessuna analisi viene compiuta su di essi e non sono neppure mostrati nel libro. Non è difficile capire perché: la loro corrispondenza con il modello BOL è bassissima. Non è lecito ignorare i dati sfavorevoli a una teoria.
  
  2) Dai 25 campioni rimanenti vengono esclusi i sei più esterni. In effetti in ogni traccia i campioni da 1 a 7 sono presi a intervalli di un metro e mezzo, con i campioni 1 e 7 in prossimità del bordo del cerchio, mentre i campioni 0 e 8 sono raccolti appena fuori dal cerchio, il più vicino possibile a 1 e 7 (così scrive Haselhoff nel rapporto, senza precisare la distanza; una mia richiesta di dettagli è rimasta senza risposta). Questo schema di campionamento è validissimo, perché il confronto diretto tra 0-8 e 1-7 consente di capire se l'allungamento dei nodi termini bruscamente al bordo del cerchio o continui ancora un po' oltre, che è quel che ci si aspetterebbe da una fonte di energia a simmetria sferica: una graduale diminuzione con l'inverso del quadrato della distanza. I dati parlano chiaro: l'allungamento cessa di colpo al bordo del cerchio. Questo fatto non è evidente a colpo d'occhio nei grafici di Haselhoff, perché, stranamente, non mostrano la linea della lunghezza media dei campioni di controllo, che agevolerebbe il confronto; inoltre, stranamente, sono a barre anziché cartesiani com'è d'uso in questi casi e quindi non mostrano le distanze reali tra i campioni. Nel libro, stranamente, sotto ogni grafico c'è perfino un diagramma di campionamento che riporta delle distanze errate tra i campioni: le distanze tra i campioni 0 e 1 e tra il 7 e l'8 sembrano uguali a tutte le altre. Alcune pagine prima, quindi in minor evidenza, c'è un diagrammino tre volte più piccolo e meno fuorviante (p. 81), ma quasi certamente ancora non in scala. Curiosamente, il testo del libro non cita la differenza di distanze, limitandosi alla seguente sibillina frase: "il campione a0 (20-25 steli), venne raccolto ad un'estremità del cerchio; i campioni a1, a2 e a3 vennero prelevati alla stessa distanza l'uno dall'altro, in direzione del centro del cerchio; a4 venne raccolto al centro; a5, a6 e a7 dalla parte opposta, allontanandosi dal centro; a8 all'estremità opposta di a0" (p. 84). Haselhoff esclude dall'analisi tutti i campioni esterni, nonostante la loro notevole rilevanza.
  
  3) I rimanenti 19 campioni vengono elaborati in modo errato, analizzandoli separatamente in tre gruppi di sette (A, B e C, con il campione centrale in comune), trovando tre diverse coppie di parametri h e k, come se si stesse parlando di tre BOL diverse. Nel modello di Haselhoff un cerchio è creato da una BOL che irradia una energia (k) a una altezza h, pertanto tre analisi separate non hanno senso. Anche così, il modello descrive meglio di una retta solo i dati di B e C: abbastanza meglio per B, meno per C. I sette campioni interni di B sono gli unici che Haselhoff mostra nelle sue pagine web "divulgative"6; tuttavia, gli altri 43 raccontano una storia diversa.
  
  

  Risultati

  
  In tab. 2 sono riportati i risultati delle analisi effettuate su entrambi i cerchi, con o senza campioni esterni (per i quali ho assunto una distanza dai campioni interni di ben 30 centimetri), a tracce separate o mettendole assieme.
  
  

  Tabella 2. In grassetto sono indicati i valori migliori (S minori o R² maggiori), in corsivo quelli relativi ad analisi prive di significato.
  Il modello BOL non funziona mai meglio di una retta, eccetto nei casi (senza senso) delle tracce B e C isolate e private dei campioni esterni. Il minimo che si possa dire è che i dati non supportano l'ipotesi BOL. Riporto in fig. 5 i dati di A, B e C e le linee della BOL e della retta che li approssimano meglio, in modo che sia possibile valutare anche a occhio quanto la BOL "salti fuori" dai dati.
  
  Qualche commento s'impone. I valori di R² per A e C divulgati da Haselhoff non coincidono con quelli in tab. 2, da me calcolati. Le differenze possono essere dovute alla rilettura dei dati dai grafici o a una procedura di ottimizzazione di h e k più accurata; i valori da me ottenuti sono infatti più favorevoli all'ipotesi BOL degli originali, quindi ritengo che queste differenze non inficino l'analisi. La differenza più marcata riguarda la traccia C: R²=0,95 (h=3,3 metri) per me, R²=0,85 (h=6,6 metri) per Haselhoff. Anch'io ottengo un valore simile (0,86) per h=6,6 metri, quindi ipotizzo che al ricercatore sia semplicemente sfuggita la combinazione di parametri migliore, che ipotizzo abbia cercato a mano, per tentativi.
  
  È interessante notare che i dati di Dreischor pubblicati nel libro presentano un R² per il modello BOL (0,549 con i campioni esterni, 0,505 senza) più alto delle tracce D, E ed F. Se quindi Haselhoff giudica "del tutto insoddisfacente" questo valore, a maggior ragione dovrebbe ritenere la stessa cosa riguardo al cerchio DEF, ma sarebbe vano cercare un'ammissione esplicita nel libro o nel rapporto.
  
  Haselhoff sottolinea la simmetria presente in ogni singola traccia, ma il fatto è che tale simmetria non corrisponde a quella del modello BOL. Haselhoff lo ammette nel report, e solo lì, suggerendo che il modello sia solo un'approssimazione di una realtà più complessa. Può darsi, ma può anche darsi che alla base di quei dati ci sia una realtà del tutto diversa. Quando e se Haselhoff avrà un modello migliore, ne riparleremo; al momento, l'asserzione che i dati supportino il modello BOL appare ingiustificata.
  
  

  Conclusioni e ipotesi

  
  A questo punto ci si può chiedere cosa effettivamente dimostrino i dati raccolti, anche prendendoli per oro colato. Non molto, in effetti:
  
  
  • le piante piegate hanno i nodi allungati;
  • l'allungamento è correlato alla distanza dal centro del cerchio;
  • c'è una certa simmetria, non perfetta e non circolare;
  • l'allungamento cessa di colpo al bordo del cerchio.
  Haselhoff presenta il punto 1 come un effetto misterioso, sostenendo che i tropismi possano sì allungare i nodi ma non così tanto in così poco tempo; al massimo, del 10-20% in una settimana (p. 84). L'unica fonte di questa stima è un esperimento di piegatura di piante condotto da Levengood2. Tuttavia, non si puo' escludere su queste basi l'intervento di fattori naturali; è noto che i tropismi dipendono molto da fattori contingenti come luce, vento, umidità, fittezza della coltivazione ^[8] e altri ancora, e la stima di Levengood è stata ottenuta in condizioni imprecisate che avrebbero potuto non essere ottimali ai fini dell'allungamento. Esistono indicazioni in tal senso? Al momento, una: il cerchio di Dreischor, fatto da persone in accordo con il proprietario del campo, dove Haselhoff ha riscontrato un allungamento del 30% dopo soli tre giorni. Stranamente, il ricercatore olandese cita Levengood ma non i suoi stessi dati. Nella tab. 3 riporto, per Hoeven e Dreischor, gli allungamenti massimi, il tempo (dichiarato) trascorso tra la formazione e la misura e infine il rapporto tra questi due numeri; si può constatare che i ritmi di allungamento calcolati non sono così diversi da suggerire meccanismi radicalmente differenti, specie considerando che neanche le condizioni di Dreischor sono note.
  
  

  Tabella 3. Dati sull'allungamento dei nodi in varie formazioni.
  
  In quanto ai punti 2 e 3, dimostrano solo che l'allungamento dipende da qualche fattore che varia da un punto all'altro del cerchio. Haselhoff scrive che una pianta non può sapere in che parte del cerchio si trova, ma quest'asserzione è un po' eccessiva. Ad esempio, l'intensità del vento può cambiare da un punto all'altro (più le piante piegate sono vicine al bordo, meno sono esposte); il vento potrebbe piegare le piante che cercano di rialzarsi, inducendo i nodi ad allungarsi ancora. Forse chi ha piegato gli steli ha calpestato maggiormente quelli al centro, stimolandone probabilmente una reazione maggiore. Potrebbe anche essere la temperatura delle piante o del suolo a cambiare; in fondo steli orizzontali intercettano la luce in modo diverso (tant'è vero che i crop circle sono nettamente visibili da notevole distanza) e, dato che il calore tende a fluire dalle regioni calde a quelle fredde, potrebbe formarsi un gradiente di temperatura tra interno ed esterno del cerchio. Potrebbe perfino essere la pioggia a essere raccolta in maniera diversa... le possibilità sono tante. Come già notato, non si può dimostrare l'inesistenza di fattori imprecisati.
  
  Passiamo al punto 4, che dimostra solo che, se fosse intervenuta una BOL, non avrebbe irradiato in tutte le direzioni ma solo sul cerchio, a cono. Non smentisce quindi l'ipotesi BOL, ma demolisce l'idea di una BOL che piega le piante con un influsso misterioso e, in aggiunta, per sua stessa natura (perché è "di luce", appunto), emette luce e radiazione in ogni direzione. No, bisogna allora pensare che l'emissione sia intenzionale, ma a che scopo, dato che di per sé non può certo piegare nulla? Per allungare i nodi e fare contenti quelli che poi li misurano?
  
  C'è poi un altro problema piuttosto grave. La tesi di Haselhoff (che era già di Levengood) è che i nodi si allunghino per dilatazione termica dei liquidi contenuti (essenzialmente acqua). Qui i casi sono due. Se il presunto riscaldamento si limitasse a scaldare un po' l'acqua senza trasformarla in vapore, i conti non tornerebbero: il coefficiente di dilatazione termica dell'acqua è di gran lunga troppo basso per giustificare gli allungamenti misurati. Se invece l'acqua arrivasse a bollire, le piante, che non sopportano più di una settantina di gradi, morirebbero subito. A tal proposito ricordo che Levengood, che ha messo piante in un forno a microonde, non ha mai scritto né che si siano allungati i nodi, né che la pianta sia sopravvissuta, né tanto meno che le due cose si siano mai verificate insieme. Del resto chi ha fatto la prova riferisce tutt'altro esito8, benché non si possa trarne una conclusione definitiva, non potendo provare in tutte le condizioni possibili: come già ricordato, non si può dimostrare su queste basi una tale asserzione negativa.
  
  Ognuno tragga le sue conclusioni. Le mie sono che i dati del cerchio di Hoeven non supportino l'ipotesi BOL e non smentiscano possibilità più "tradizionali" come l'uso di corde e assi.
  
  

  Bibliografia

  
  
  1) Levengood, W. C. 1994. "Anatomical anomalies in crop formation plants". Physiologia Plantarum 92: pp. 356-363. www.ecn.org/cunfi/Levengood1994.pdf
  2) Levengood, W. C., Talbott, N.P. 1999. "Dispersion of energies in worldwide crop formations". Physiologia Plantarum 105: pp. 615-624. www.ecn.org/cunfi/LevengoodandTalbott1999.pdf
  3) Haselhoff, E. H. 2001. "Opinions and comments on Levengood WC, Talbott NP (1999) Dispersion of energies in worldwide crop formations. Physiol Plant 105: 615-624". Physiologia Plantarum 111: pp. 123-125. www.ecn.org/cunfi/Haselhoff.pdf
  4) Grassi, F., Cocheo, C., Russo, P. 2005. "Balls of Light: The Questionable Science of Crop Circles". Journal of Scientific Exploration (19) 2: pp. 159-170. www.cicap.org/crops/jse_19_2_159-170_2005.pdf
  5) Haselhoff, E. H. 2002. La natura complessa dei cerchi nel grano, Reggio Emilia: Natrix Edition.
  6) Haselhoff, E. H. 1999. Node Length Measurement. www.dcccs.org/node_length_measurements.htm anche come: Haselhoff, E. H. 1999. Hoeven Report. www.dcccs.org/hoeven_report.htm
  7) Tipiche pagine web "divulgative", in inglese e in italiano:

Haselhoff, E. H. Scientific Studies Confirm: Crop Circles Made by "Balls of Light". www.dcccs.org/bols.htm Haselhoff, E. H. GLI STUDI SCIENTIFICI CONFERMANO: i Cerchi nel Grano sono creati da "Sfere di Luce". www.natrix.it/articoli/scienza/cng/S-cng-027/main.htm