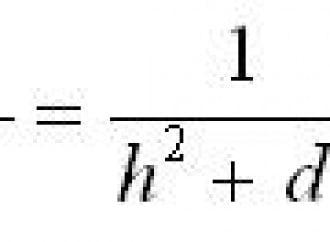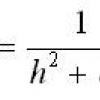La storia ufficiale delle misteriose impronte circolari che compaiono periodicamente nelle coltivazioni cominciò nel 1980 quando l'attenzione del dottor Terence Meaden fu attirata da una formazione apparsa in un campo di avena vicino a Bratton (Inghilterra), ai piedi dei ripidi pendii erbosi dove è disegnato il famoso Cavallo Bianco di Westbury.
Questi "primi" cerchi furono chiamati "cerchi misteriosi" o semplicemente "anelli", ma a partire circa dal 1988 vennero indicati in tutto il mondo con il termine "cerchi nel grano" (crop circles, alla lettera "cerchi nelle coltivazioni"). I cerchi nel grano consistono in regioni geometriche all'interno delle coltivazioni, in cui le piante (soprattutto cereali) sono appiattite in posizione orizzontale.
Nel corso degli anni i cerchi nel grano guadagnarono sempre più l'attenzione dei mass media, evolvendo da semplici strutture circolari a figure sempre più complesse, e il loro numero crebbe da alcune dozzine agli inizi della loro apparizione documentata, a centinaia solo pochi anni dopo. Negli anni Ottanta e Novanta, ad esempio, il numero di cerchi apparsi in Gran Bretagna aumentò rapidamente da una manciata per anno nei primi anni Ottanta a dozzine a fine del decennio e a centinaia già nel 1991.
Nel corso degli anni in molti ammisero di aver creato personalmente dei cerchi ma, nonostante queste confessioni, i "credenti" continuarono a rifiutare l'idea del coinvolgimento umano come sola spiegazione dell'origine del fenomeno. Proliferarono così numerose teorie alternative nel tentativo di spiegare le possibili cause non-umane della creazione dei cerchi. La maggior parte delle affermazioni fu costituita nient'altro che da semplici ipotesi le quali non guadagnarono una credibilità sufficiente a superare l'esame di riviste scientifiche referate.
Solo tre studi ottennero la pubblicazione su una rivista scientifica: il primo a firma di W.C. Levengood (1994), il secondo di W.C. Levengood e N.P. Talbott (1999) e l'ultimo di E.H. Haselhoff (2001). Tutti e tre gli articoli suggerivano il coinvolgimento di una qualche forma di radiazione elettromagnetica nella creazione dei cerchi. Tuttavia nessuno dei tre forniva una lista di condizioni sufficienti (o perlomeno necessarie) per stabilire senza dubbio se una data formazione fosse o meno opera dell'uomo.
Levengood (1994) affermò di aver trovato nelle formazioni delle alterazioni anatomiche (le cosiddette "anomalie") che non potevano essere spiegate assumendo un'origine antropica dei cerchi. Tra le altre anomalie, che non discutiamo in questo articolo, egli osservò una presunta espansione anomala dei nodi degli steli delle piante che si trovavano all'interno dei cerchi rispetto a quelle poste all'esterno (si tratta del cosiddetto a-test, cioè del rapporto fra la lunghezza dello stelo e del nodo). Levengood concluse che queste alterazioni erano probabilmente causate da un effetto termomeccanico dovuto all'espansione delle pareti cellulari, direttamente legato a un assorbimento di energia elettromagnetica. Nel corso di un esperimento condotto nel Maryland nel 1997, Levengood e Talbott (1999) realizzarono essi stessi un cerchio, giungendo alla conclusione che la risposta gravitropica non superava il 10% a tre giorni dalla creazione del cerchio; troppo poco, secondo loro, per spiegare gli allungamenti osservati nelle presunte formazioni "genuine". Discuteremo in seguito questa affermazione.
Nel 1999 Levengood e Talbott pubblicarono i risultati di un campionamento eseguito su tre semplici formazioni circolari apparse a Devizes (Inghilterra, 1993), Chehalis (Washington, USA, 1994) e nel Sussex (Inghilterra, 1994). Riportarono inoltre un quarto caso in cui analizzarono una formazione più complessa, a forma di spirale, che comparve in un campo di orzo a Beckhampton (Inghilterra) nel 1995.
È importante sottolineare come due dei tre cerchi apparvero in zone in cui vivevano e operavano da almeno un decennio numerosi circlemakers. La formazione di Devizes comparve in un'area vicina a Beckhampton, Wiltshire, e vicina a Bratton dove nel 1990 apparve il più famoso falso crop circle ("Operazione Blackbird"), dove nel 1983 fu creato uno dei primi falsi con la sponsorizzazione di alcuni quotidiani nazionali, dove ha vissuto e operato, dal 1990 al 1991, uno dei principali gruppi di circlemakers noto come "United Bureau of Investigation" e dove nei primi anni Novanta i Wessex Skeptics crearono appositamente delle formazioni per mettere alla prova i ricercatori dei cerchi nel grano. La formazione del Sussex apparve in una zona in cui la diffusione di "falsi" cerchi nei raccolti era meno evidente rispetto a Beckhampton, ma dove vivevano numerosi potenziali circlemakers. I campioni furono raccolti in un'area in cui, come anche i ricercatori sui cerchi nel grano più inclini all'ipotesi paranormale dovettero in seguito ammettere, la diffusione di hoax era elevata. Questi campioni inoltre erano stati raccolti vicino alle due regioni in cui Doug Bower e Dave Chorley avevano probabilmente iniziato a creare cerchi nel grano già dagli anni Ottanta (South Wiltshire, Alfriston, East Sussex). Entrambe le zone sembrano aver attratto numerosi emuli degli originali cerchi di Doug e Dave.
Levengood e Talbott raccolsero, per ogni posizione di misura, gruppi di 10-15 piante a distanze crescenti dal centro del cerchio e, per ciascun gruppo, calcolarono il valor medio della lunghezza dei nodi. Confrontando in grafico il logaritmo delle lunghezze medie di gruppo dei nodi con la distanza dal centro, essi individuarono una relazione lineare fra le due variabili. Quindi, la lunghezza dei nodi sembrava decrescere con legge esponenziale negativa, dal centro delle aree appiattite verso i bordi.
Gli autori suggerirono che questo andamento si accordava con un assorbimento di energia elettromagnetica dovuto a un fronte d'onda piano incidente sulle piante dopo essersi propagato in aria seguendo la legge di Beer-Lambert.
Essi descrissero la relazione fra la lunghezza dei nodi e l'intensità della radiazione incidente come:
NL = b(I/I0) = b(e-acd)
dove NL è la lunghezza dei nodi, b una costante di proporzionalità, I l'intensità della radiazione alla distanza d dalla sorgente, I0 l'intensità della radiazione alla sorgente, a il coefficiente di assorbimento dell'aria e c la concentrazione delle molecole assorbenti.
Due anni dopo Haselhoff commentò l'articolo, mettendo in evidenza, in particolare, due errori: la lunghezza dei nodi degli steli normali era stata assunta uguale a zero e non si era tenuto conto della dispersione dell'energia all'aumentare della distanza. Egli pertanto suggerì di correggere il primo errore sottraendo un termine N0, che rappresenta la lunghezza media dei nodi delle piante esterne alle formazioni ("controlli") non affette quindi dal presunto irraggiamento. In tal modo egli accettava implicitamente sia la discutibile strategia di campionamento degli esperimenti di Levengood e Talbott, sia l'ipotesi termomeccanica come spiegazione per l'allungamento dei nodi.
L'articolo di Haselhoff si focalizzava su un nuovo modello di propagazione della presunta radiazione elettromagnetica che sarebbe stata coinvolta a suo parere nella creazione dei cerchi. Analizzando i dati raccolti nei primi tre cerchi sopra menzionati, Haselhoff identificò un andamento quadratico inverso nell'allungamento dei nodi all'aumentare della distanza radiale. Propose quindi un modello basato su una sorgente di radiazione puntiforme, definendola come una "Sfera di Luce" (Ball of Light - BOL) che irraggiasse la coltura sottostante.
Per dare maggior consistenza alla sua ipotesi Haselhoff riportò, come controprova, i risultati di uno studio condotto su una formazione di sicura origine umana, comparsa a Nieuwerkerk nel 1997, nella quale lo stesso andamento quadratico non sembrava evidente.
L'ipotesi BOL consiste in un modello che descrive la diminuzione, con il crescere della distanza, dell'intensità di un fronte d'onda sferico di radiazione elettromagnetica originato da una sorgente puntiforme posta ad un'altezza finita h sopra il campo (fig. 1).
Sebbene non esplicitamente indicata nel testo dell'articolo di Haselhoff, l'equazione del modello può essere dedotta da semplici considerazioni fisiche, assumendo una decrescita 1/r2 dell'intensità della radiazione moltiplicato per una costante di proporzionalità, secondo la relazione:
NL - N0 = b/r2
dove b è la costante di proporzionalità e r2 = d2 + h2, dove d è la distanza proiettata al suolo del punto dal centro del cerchio e h l'altezza dell'ipotetica sorgente dal centro del cerchio. Per ogni formazione il parametro h fu ottimizzato per regredire al meglio i dati secondo l'andamento 1/r2. Riscalando l'asse delle x secondo 1/r2 e scegliendo NL-N0 come ordinate, se l'ipotesi BOL fosse corretta ci si dovrebbe attendere un elevato valore del coefficiente di correlazione R2.
Sia per i sensazionali contenuti scientifici, sia per lo straordinario impatto esercitato sulla pubblica opinione, sembra necessaria un'analisi più dettagliata sul trattamento dei dati e sull'analisi statistica, in base alla regola che affermazioni straordinarie richiedono prove altrettanto straordinarie.
Prima di iniziare la trattazione riteniamo importante evidenziare come i tre articoli sopra menzionati siano di fatto considerati il "punto di riferimento scientifico" per la comunità delle persone interessate al fenomeno dei crop circles. Physiologia Plantarum Journal giocò un ruolo cruciale, pubblicando tutti e tre gli articoli e fornendo agli autori supporto e credibilità scientifica. Inoltre, il nostro articolo fu dapprincipio sottoposto a Physiologia Plantarum Journal e l'editore si dichiarò d'accordo con i nostri commenti sulla pseudoscientificità dei contenuti dei tre articoli (Physiologia Plantarum Journal, comunicazione agli autori, 2004), ma rifiutò la pubblicazione del nostro articolo con la sorprendente motivazione secondo la quale "non c'è alcun dibattito scientifico in atto su questo argomento".
La nostra prima critica all'articolo di Haselhoff riguarda la strategia di campionamento e l'approccio statistico. Sia il numero di formazioni esaminate, sia il numero di dati raccolti all'interno e all'esterno di ciascuna di esse sono inadeguati per eseguire un'analisi statistica attendibile .
È significativo osservare (vedi Tab.1) come, nel suo articolo del 2001 su Physiologia Plantarum, non sia riportato il numero di campioni raccolti nei vari siti. Omissione piuttosto sorprendente, considerato che la maggior parte delle pubblicazioni scientifiche indica la dimensione della popolazione campionata, in modo da poter dimostrare che le conclusioni statistiche a cui giungono non si fondano su un insieme di pochi dati. Questa è una considerazione importante, perché l'articolo di Haselhoff su Physiologia Plantarum del 2001 sostiene chiaramente che il fenomeno che essi dichiarano di aver scoperto si applica a molti cerchi, non a pochi. Nel caso della formazione di Chehalis, per esempio, i campioni sono stati raccolti solo in tre posizioni e non stupisce che un modello a due parametri possa fornire una regressione apparentemente buona per tre punti, sebbene ciò non indichi una relazione causa-effetto.
Tabella 1. Dati sperimentali per le formazioni di Devizes, Chehalis e Sussex. d è la distanza della posizione di misura da centro del cerchio; Nl è la lunghezza media dei nodi; l'apice c indica dati appartenenti ai ciuffi centrali; l'apice e indica dati raccolti all'esterno delle formazioni.
La BOL è un modello di regressione a due parametri: l'altezza h dal suolo e la costante di proporzionalità b. Il parametro b non è così insignificante da meritare di essere superficialmente trascurato, come è stato fatto nell'articolo di Haselhoff, ma dovrebbe giocare un ruolo cruciale nel processo fisico sottostante. In realtà il parametro b contiene tutte le informazioni non geometriche del fenomeno. Piuttosto che una costante esso rappresenta, in effetti, un insieme di più variabili. Esso descrive tutte le proprietà fisiche del fenomeno come, per esempio, la durata dell'irraggiamento, l'intervallo spettrale della radiazione emessa, l'intensità della sorgente, l'assorbimento dell'aria, il contenuto di umidità delle piante e del suolo circostante, le proprietà assorbenti e riflettenti delle piante e del suolo e così via.
Per le formazioni di Devizes e Chehalis, entrambe all'interno di coltivazioni di frumento, abbiamo trovato rispettivamente b=10,3 e b=68,9; si tratta di valori ben diversi. Haselhoff non solo ha omesso di spiegare il significato dei parametri e la ragione delle loro differenze, ma ne ha omesso anche la pubblicazione dei valori. In particolare, solo l'altezza h della BOL dal suolo è riportata nella tabella 1 dell'articolo di Haselhoff. Ne segue che il modello sembra possedere un solo parametro, l'altezza h, fornendo dei risultati sorprendentemente buoni per un modello a un solo parametro.
Un altro aspetto criticabile riguarda la mancanza di un protocollo standardizzato per stabilire quali misure includere nel gruppo di controllo. Alcune piante rimaste erette molto lontano dalle formazioni furono definite come "controlli" e considerate come piante indisturbate; i loro valori medi e le deviazioni standard furono calcolate in modo da permettere il paragone tra piante affette e piante non affette. Le piante appiattite all'interno dei cerchi furono considerate "affette" (cioè non-controlli). In realtà, anche alcune piante erette, raccolte all'esterno dei cerchi, furono considerate "affette" e non classificate nel gruppo di controllo: due campioni nella formazione del Sussex furono raccolti a 6 e 14 metri dal limite esterno del cerchio e un campione a Devizes fu raccolto 30 centimetri oltre il bordo della formazione (figure 2a e 2c). Nessuna giustificazione relativamente a questa decisione è stata addotta nell'articolo. Nessuna distanza limite per l'inclusione o meno dei campioni nei gruppi di controllo è menzionata. Dobbiamo supporre che gli autori abbiano deciso di assegnare queste piante al gruppo delle "affette" piuttosto che a quello dei controlli dopo aver osservato che i loro allungamenti erano maggiori di quelli delle piante definite "controllo". Questa è una procedura che può generare artefatti.
Ci potrebbero essere delle ragioni per includere alcune piante rimaste erette all'esterno dei cerchi nel gruppo delle piante "affette", dato che gli autori sembrano indagare su effetti che potrebbero non essere strettamente limitati all'area del raccolto abbattuto al suolo. Tuttavia, se nessun criterio oggettivo viene stabilito chiaramente e a priori, ogni analisi successiva diventa discutibile, perché la deviazione standard dei controlli può essere sottostimata, rendendo i valori degli allungamenti dei nodi delle piante "affette" apparentemente più anomali di quanto essi siano.
Inoltre, se il bordo del cerchio non è assunto come criterio discriminante, diventa più complicato assicurarsi che gli effetti che si stanno investigando siano realmente provocati dal fenomeno che ha generato il cerchio, piuttosto che da altre cause concorrenti. Questo è particolarmente rilevante se si considera che, a causa dello scarso numero di campioni raccolti, l'analisi manca di risoluzione spaziale e che le piante di controllo sono state raccolte solo a grandi distanze dal bordo dei cerchi, dove le condizioni ambientali potrebbero essere state un po' diverse. Nessun test statistico per confrontare le medie e le varianze dei campioni presi all'interno e all'esterno delle formazioni è stato applicato. Qualsiasi conclusione fondata sul paragone fra campioni raccolti all'interno dei cerchi e quelli provenienti dal resto del raccolto non è, quindi, supportata da un'analisi statistica robusta.
La figura 2 mostra le misure effettuate nelle tre formazioni di Devizes (a), Chehalis (b) e Sussex (c). I raggi dei tre cerchi furono rispettivamente di 3, 6 e 9 metri e tutte le piante rimaste erette all'esterno avrebbero dovuto essere considerate come campioni di controllo, a meno che non venisse dichiarato un diverso criterio.

Ciò nonostante, il primo punto a destra nel grafico di Devizes e i primi due in quello del Sussex furono inclusi nel modello di regressione sia da Levengood e Talbott che da Haselhoff, nonostante la loro reale natura di controlli. Particolarmente sorprendente è il caso del Sussex, in cui l'intervallo di confidenza del gruppo di controllo è molto piccolo mentre uno dei campioni (controllo) si trova ben al di fuori di esso. Chiaramente questo punto fu escluso dal calcolo della deviazione standard dei livelli di controllo, conducendo a una sottostima del reale valore e rendendo, quindi, impossibile un confronto attendibile fra la variabilità degli allungamenti dei nodi delle piante interne al cerchio e di quelle appartenenti al resto della coltivazione.
Nelle formazioni del Sussex e di Chehalis furono rinvenuti ciuffi circolari di piante rimaste erette al centro dei cerchi, eppure questi campioni furono esclusi dall'analisi della regressione del modello, nonostante si trovassero nel cuore dei cerchi e nonostante l'importanza di questi campioni vista la loro prossimità alla presunta sorgente radiante. Levengood e Talbott esclusero il ciuffo centrale sebbene, grazie all'omissione del fattore di dispersione dell'energia, questo non costituisse alcuna singolarità per il loro modello esponenziale. Sebbene Haselhoff possa aver escluso i ciuffi centrali con l'obiettivo di confrontare i propri risultati con quelli di Levengood e Talbott, egli avrebbe dovuto includerli al fine di valutare correttamente le prestazioni del suo modello.
Inoltre critichiamo la mancanza di informazioni sulla significatività statistica dei parametri del modello proposto. Questo tipo di valutazione è imprescindibile perché permette di giudicare l'attendibilità della regressione, basata sulla trasformazione dell'asse x in seguito all'ottimizzazione del parametro h. Ripetendo le analisi di regressione di Haselhoff sui dati originali, abbiamo scoperto che il parametro h non è significativo al livello a=0,05 (tabella 2a), che costituisce già un limite piuttosto generoso per un'affermazione tanto clamorosa. Includendo i ciuffi centrali nei dati, peggiorano sia i coefficienti di correlazione R2 sia la significatività statistica di h (tabella 2a); pertanto, il modello BOL appare statisticamente privo di attendibilità o, perlomeno, non sufficientemente significativo da ritenere ragionevole l'esistenza di una sorgente puntiforme di radiazione elettromagnetica che irraggi dall'alto i cerchi nel grano.

Va sottolineato come una semplice regressione lineare, che ha lo stesso numero di parametri, approssimi i dati meglio di quanto faccia il modello BOL (tabella 2b). Naturalmente, non stiamo suggerendo l'esistenza di uno specifico sottostante fenomeno lineare, ma vogliamo semplicemente mettere in luce un concetto basilare: l'esistenza di una correlazione non è necessariamente indice di un nesso di causalità. In aggiunta, è molto importate sottolineare che l'applicazione di test statistici a un numero così scarso di dati può condurre a conclusioni errate che sono ben lungi dall'essere statisticamente significative.

Il modello BOL, inoltre, è irrealistico anche da un punto di vista fisico. Un ipotetico modello BOL dovrebbe essere molto più complesso, perché la quantità di energia che colpisce le piante dovrebbe dipendere dall'angolo di incidenza della radiazione rispetto ai nodi degli steli e l'assorbimento di energia dipenderebbe dal cammino percorso dalla radiazione all'interno delle piante e, di conseguenza, dalla loro effettiva trasparenza. Uno stelo parzialmente trasparente schermerebbe in parte il nodo; ne conseguirebbe che il modello di Haselhoff potrebbe funzionare solo assumendo che le piante fossero del tutto trasparenti alla radiazione e pertanto non potrebbero assorbire alcuna energia. Quindi, se ci fosse davvero una sorgente puntiforme ad irraggiare i raccolti, la sua impronta non mostrerebbe comunque un andamento 1/r2.
Abbiamo ottenuto da Haselhoff (Haselhoff, comunicazione agli autori, 2003) le misure originali raccolte nella formazione di origine umana di Nieuwerkerk (fig. 3) e le abbiamo confrontate con quanto riportato nell'articolo di Haselhoff.

La prima cosa che osservammo fu che gli allungamenti dei nodi arrivavano sino al 30%, contraddicendo le conclusioni dell'esperimento di Levengood e Talbott nel Maryland (1997), in cui si stimò che il gravitropismo ammontasse a non più del 10%, e dimostrando nel contempo che piante prelevate in formazioni di dichiarata origine umana potevano presentare allungamenti confrontabili con quelli di piante raccolte in formazioni considerate non antropogeniche ("genuine").
Esaminando il caso di Nieuwerkerk, inoltre, notammo che questa volta il primo punto esterno al cerchio era stato escluso dall'analisi, nonostante distasse appena 10 centimetri dal bordo del cerchio (cioè 12,8 metri dal centro). Includendo questo punto nella regressione, come necessario per eseguire un confronto coerente con le analisi eseguite sulle altre formazioni "genuine", il coefficiente di correlazione del modello BOL cambia da R=0,54 a R=0,63.
La cosa più sorprendente, tuttavia, fu scoprire che solo una parte delle misure sperimentali era stata pubblicata nell'articolo. Durante l'esperimento, Haselhoff raccolse due serie di misure, chiamate set A e set B, raccogliendo i campioni secondo due direttrici perpendicolari fra loro sulla stessa impronta circolare, ma pubblicò i risultati del solo set A. Il coefficiente di correlazione del modello BOL applicato al set B è R=0,71, decisamente più alto di quello del set A.
Usando entrambi i set, mediando i valori dei punti che si trovavano all'interno del cerchio, alla stessa distanza dal centro (fig. 2d), trovammo che il coefficiente di correlazione per il modello BOL cresce a R=0,73. Inoltre, includendo tutti i dati disponibili appartenenti alla parte esterna dei cerchi e usando come valore di controllo la media di tutti i punti esterni, il coefficiente di correlazione sale a R=0,83. In conclusione: piante raccolte in formazioni di dichiarata origine umana possono rivelare proprietà statistiche simili a quelle di formazioni considerate "genuine".
Un'altra critica riguarda la mancanza di analisi della formazione a spirale di Beckhampton, sebbene questo esperimento fosse stato dettagliatamente descritto nell'articolo di Levengood e Talbott, lo stesso articolo commentato da Haselhoff. In realtà, la formazione di Beckhampton non presenta alcun andamento 1/r2; gli allungamenti dei nodi non sembrano neppure correlati con la distanza dal centro. Ricordiamo che tutti gli esperimenti devono essere presi in considerazione e che una teoria è valida solo quando è in grado di spiegare tutti i casi e non solo quelli che si accordano con l'ipotesi sperimentale.
Si potrebbe ipotizzare che, per riuscire a tracciare una spirale nel raccolto, una BOL avrebbe dovuto muoversi in modo complesso piuttosto che stazionare semplicemente sopra il centro; questo movimento complesso impedirebbe di scorgere nei dati l'andamento 1/r2, rendendo chiare le ragioni dell'esclusione dall'analisi.
Tuttavia, questa giustificazione condurrebbe a porsi domande circa la portata dei tre articoli. È normalmente accettato dai "credenti" che i cerchi nel grano siano opera di esseri senzienti, perché (presumibilmente) i fenomeni naturali non sarebbero in grado di generare una tale varietà di figure geometriche dall'apparenza così simbolica. Queste avvincenti proprietà geometriche non sono però presenti nelle semplici forme circolari o in quelle irregolari (non-geometriche). Se una pubblicazione scientifica si focalizza solo sui semplici cerchi, le sue conclusioni non possono poi essere estese alle formazioni complesse se non affidandosi alla discutibile implicita assunzione che possa esistere una sola unica causa per l'abbattimento delle piante. Se un articolo scientifico non prende in considerazione anche le formazioni complesse allora la sua rilevanza nei confronti di ciò che la gente chiama "cerchi nel grano" rimane tutta da dimostrare.
Un'altra critica fondamentale riguarda l'inconsistenza delle assunzioni. Nell'articolo di Levengood e Talbott è suggerito che l'allungamento dei nodi sia dovuto ad un rapido e intenso riscaldamento dei tessuti delle piante, conseguente all'assorbimento di radiazione elettromagnetica. Il riscaldamento dell'acqua contenuta nelle cellule sarebbe all'origine di un aumento di pressione interna che, a sua volta, forzerebbe i tessuti visco-elastici ad allungarsi. Nel suo articolo, pubblicato nel 1994, Levengood sostenne che "se energia da microonde è coinvolta nella formazione dei crop circles, la quantità di calore dovrebbe dipendere dal contenuto d'acqua della pianta". La dilatazione termica dell'acqua liquida fra 15 °C e 90 °C, tuttavia, è non più del 3,5%, non sufficiente a giustificare gli allungamenti tra il 30% e il 200% osservati per i nodi nelle formazioni (Levengood & Talbott, 1999).
Inoltre, sia Levengood e Talbott (1999) che J.A. Burke (1998), un membro dello stesso gruppo di ricerca (BLT), affermarono che danni alle piante (allungamenti dei nodi) di maggior entità si rinvengono in piante abbattute al suolo a causa del vento o di condizioni meteorologiche severe.
Tutte le ipotesi formulate attorno alla creazione dei cerchi si fondano su un effetto termomeccanico, ma nessuno degli autori ha mai dimostrato la possibilità per i nodi di potersi allungare sino del 200% o anche del 100%, così come osservato nelle formazioni "genuine", sotto l'azione di un riscaldamento. Eppure non sembra difficile verificare se i nodi possano effettivamente allungarsi sotto l'azione di calore radiante (senza bruciare o uccidere le piante); ma finché una qualche evidenza di laboratorio per l'effetto termomeccanico non viene prodotta, allungamenti dei nodi come quelli dichiaratamente osservati nei cerchi nel grano non possono essere collegati all'assorbimento di una qualche forma di irraggiamento elettromagnetico.
Un'altra critica riguarda la mancanza di informazioni dettagliate su ogni argomento trattato negli articoli: nessuna fotografia delle tre formazioni genuine, né del "falso" di Nieuwerkerk è stata prodotta; nessuna tabella con i dati originali è stata riportata; non è stata fornita alcuna descrizione sulla geometria dell'appiattimento delle piante (cioè nulla è stato detto sulla posizione delle piante abbattute); nulla è stato scritto sulla posizione in cui i campioni sono stati raccolti all'interno del cerchio, tranne la loro distanza dal centro. Quindi lo studio non permette un'analisi bidimensionale; nessuna incertezza sul valore delle ascisse è riportata, laddove ogni punto di campionamento rappresentava in effetti la lunghezza media dei nodi di circa 10-15 piante e piccole differenze nella distanza dal centro producono enormi variazioni nell'allungamento dei nodi, come nel caso della formazione di Devizes in cui il secondo e terzo punto distavano solo 1,9 cm eppure gli allungamenti differiscono addirittura dell'86%. Nessuna ipotesi è stata formulata su ciò che riguarda la durata, l'intensità e la frequenza della presunta radiazione. Infine, l'opacità delle piante alla radiazione, che implica la necessità di considerazioni sugli angoli di incidenza, può drammaticamente modificare la simmetria del meccanismo di assorbimento di energia e, quindi, l'equazione del modello; questo elemento è stato del tutto ignorato.
La nostra conclusione è che le affermazioni sul coinvolgimento di una qualche forma di irraggiamento elettromagnetico all'origine della formazione dei cerchi nel grano non trova supporto nell'evidenza sperimentale. In particolare, l'andamento 1/r2 esiste solo in virtù di un'esclusione ingiustificata di dati indesiderati; nonostante ciò, anche in queste condizioni privilegiate, il modello proposto non interpola i dati altrettanto bene quanto una semplice regressione lineare. E seppure un andamento 1/r2 fosse evidenziabile nei dati sperimentali, esso non potrebbe comunque essere attribuito ad una sorgente puntiforme di radiazione, perché implicherebbe la completa trasparenza delle piante rispetto alla radiazione incidente, impedendo qualunque assorbimento di energia. Inoltre, il modello BOL è stato selettivamente applicato alle sole formazioni dalla struttura circolare semplice, laddove le forme rettangolari o più complesse sono state deliberatamente ignorate per l'impossibilità di adattarle all'ipotesi BOL.
I fatti discussi nel nostro articolo critico non dimostrano nient'altro che l'esistenza di una semplice differenza nell'allungamento dei nodi delle piante abbattute all'interno dei cerchi rispetto a quelle rimaste erette al loro esterno, come ci si dovrebbe attendere nel caso in cui un qualunque tipo di azione meccanica riuscisse ad appiattire al suolo le piante, corde e assi comprese.
Francesco Grassi
Ingegnere,
Gruppo sperimentazioni CICAP
Claudio Cocheo
Centro di Ricerche Ambientali,
Fondazione Salvatore Maugeri, CICAP Veneto
Paolo Russo
Programmatore, CICAP Friuli Venezia Giulia
Tutti e tre fanno parte del Gruppo di Ricerca del CICAP sui Crop Circles Traduzione italiana a cura di Claudio Cocheo pubblicata su Scienza & Paranormale (S&P N. 63 - Anno XIII -Set/Ott 2005) dell'articolo originale in inglese pubblicato su Journal of Scientific Exploration Vol. 19, n.2, pp. 159-170, 2005 (PDF version)
Questi "primi" cerchi furono chiamati "cerchi misteriosi" o semplicemente "anelli", ma a partire circa dal 1988 vennero indicati in tutto il mondo con il termine "cerchi nel grano" (crop circles, alla lettera "cerchi nelle coltivazioni"). I cerchi nel grano consistono in regioni geometriche all'interno delle coltivazioni, in cui le piante (soprattutto cereali) sono appiattite in posizione orizzontale.
Nel corso degli anni i cerchi nel grano guadagnarono sempre più l'attenzione dei mass media, evolvendo da semplici strutture circolari a figure sempre più complesse, e il loro numero crebbe da alcune dozzine agli inizi della loro apparizione documentata, a centinaia solo pochi anni dopo. Negli anni Ottanta e Novanta, ad esempio, il numero di cerchi apparsi in Gran Bretagna aumentò rapidamente da una manciata per anno nei primi anni Ottanta a dozzine a fine del decennio e a centinaia già nel 1991.
Nel corso degli anni in molti ammisero di aver creato personalmente dei cerchi ma, nonostante queste confessioni, i "credenti" continuarono a rifiutare l'idea del coinvolgimento umano come sola spiegazione dell'origine del fenomeno. Proliferarono così numerose teorie alternative nel tentativo di spiegare le possibili cause non-umane della creazione dei cerchi. La maggior parte delle affermazioni fu costituita nient'altro che da semplici ipotesi le quali non guadagnarono una credibilità sufficiente a superare l'esame di riviste scientifiche referate.
Solo tre studi ottennero la pubblicazione su una rivista scientifica: il primo a firma di W.C. Levengood (1994), il secondo di W.C. Levengood e N.P. Talbott (1999) e l'ultimo di E.H. Haselhoff (2001). Tutti e tre gli articoli suggerivano il coinvolgimento di una qualche forma di radiazione elettromagnetica nella creazione dei cerchi. Tuttavia nessuno dei tre forniva una lista di condizioni sufficienti (o perlomeno necessarie) per stabilire senza dubbio se una data formazione fosse o meno opera dell'uomo.
Levengood (1994) affermò di aver trovato nelle formazioni delle alterazioni anatomiche (le cosiddette "anomalie") che non potevano essere spiegate assumendo un'origine antropica dei cerchi. Tra le altre anomalie, che non discutiamo in questo articolo, egli osservò una presunta espansione anomala dei nodi degli steli delle piante che si trovavano all'interno dei cerchi rispetto a quelle poste all'esterno (si tratta del cosiddetto a-test, cioè del rapporto fra la lunghezza dello stelo e del nodo). Levengood concluse che queste alterazioni erano probabilmente causate da un effetto termomeccanico dovuto all'espansione delle pareti cellulari, direttamente legato a un assorbimento di energia elettromagnetica. Nel corso di un esperimento condotto nel Maryland nel 1997, Levengood e Talbott (1999) realizzarono essi stessi un cerchio, giungendo alla conclusione che la risposta gravitropica non superava il 10% a tre giorni dalla creazione del cerchio; troppo poco, secondo loro, per spiegare gli allungamenti osservati nelle presunte formazioni "genuine". Discuteremo in seguito questa affermazione.
Nel 1999 Levengood e Talbott pubblicarono i risultati di un campionamento eseguito su tre semplici formazioni circolari apparse a Devizes (Inghilterra, 1993), Chehalis (Washington, USA, 1994) e nel Sussex (Inghilterra, 1994). Riportarono inoltre un quarto caso in cui analizzarono una formazione più complessa, a forma di spirale, che comparve in un campo di orzo a Beckhampton (Inghilterra) nel 1995.
È importante sottolineare come due dei tre cerchi apparvero in zone in cui vivevano e operavano da almeno un decennio numerosi circlemakers. La formazione di Devizes comparve in un'area vicina a Beckhampton, Wiltshire, e vicina a Bratton dove nel 1990 apparve il più famoso falso crop circle ("Operazione Blackbird"), dove nel 1983 fu creato uno dei primi falsi con la sponsorizzazione di alcuni quotidiani nazionali, dove ha vissuto e operato, dal 1990 al 1991, uno dei principali gruppi di circlemakers noto come "United Bureau of Investigation" e dove nei primi anni Novanta i Wessex Skeptics crearono appositamente delle formazioni per mettere alla prova i ricercatori dei cerchi nel grano. La formazione del Sussex apparve in una zona in cui la diffusione di "falsi" cerchi nei raccolti era meno evidente rispetto a Beckhampton, ma dove vivevano numerosi potenziali circlemakers. I campioni furono raccolti in un'area in cui, come anche i ricercatori sui cerchi nel grano più inclini all'ipotesi paranormale dovettero in seguito ammettere, la diffusione di hoax era elevata. Questi campioni inoltre erano stati raccolti vicino alle due regioni in cui Doug Bower e Dave Chorley avevano probabilmente iniziato a creare cerchi nel grano già dagli anni Ottanta (South Wiltshire, Alfriston, East Sussex). Entrambe le zone sembrano aver attratto numerosi emuli degli originali cerchi di Doug e Dave.
Levengood e Talbott raccolsero, per ogni posizione di misura, gruppi di 10-15 piante a distanze crescenti dal centro del cerchio e, per ciascun gruppo, calcolarono il valor medio della lunghezza dei nodi. Confrontando in grafico il logaritmo delle lunghezze medie di gruppo dei nodi con la distanza dal centro, essi individuarono una relazione lineare fra le due variabili. Quindi, la lunghezza dei nodi sembrava decrescere con legge esponenziale negativa, dal centro delle aree appiattite verso i bordi.
Gli autori suggerirono che questo andamento si accordava con un assorbimento di energia elettromagnetica dovuto a un fronte d'onda piano incidente sulle piante dopo essersi propagato in aria seguendo la legge di Beer-Lambert.
Essi descrissero la relazione fra la lunghezza dei nodi e l'intensità della radiazione incidente come:
NL = b(I/I0) = b(e-acd)
dove NL è la lunghezza dei nodi, b una costante di proporzionalità, I l'intensità della radiazione alla distanza d dalla sorgente, I0 l'intensità della radiazione alla sorgente, a il coefficiente di assorbimento dell'aria e c la concentrazione delle molecole assorbenti.
Due anni dopo Haselhoff commentò l'articolo, mettendo in evidenza, in particolare, due errori: la lunghezza dei nodi degli steli normali era stata assunta uguale a zero e non si era tenuto conto della dispersione dell'energia all'aumentare della distanza. Egli pertanto suggerì di correggere il primo errore sottraendo un termine N0, che rappresenta la lunghezza media dei nodi delle piante esterne alle formazioni ("controlli") non affette quindi dal presunto irraggiamento. In tal modo egli accettava implicitamente sia la discutibile strategia di campionamento degli esperimenti di Levengood e Talbott, sia l'ipotesi termomeccanica come spiegazione per l'allungamento dei nodi.
L'articolo di Haselhoff si focalizzava su un nuovo modello di propagazione della presunta radiazione elettromagnetica che sarebbe stata coinvolta a suo parere nella creazione dei cerchi. Analizzando i dati raccolti nei primi tre cerchi sopra menzionati, Haselhoff identificò un andamento quadratico inverso nell'allungamento dei nodi all'aumentare della distanza radiale. Propose quindi un modello basato su una sorgente di radiazione puntiforme, definendola come una "Sfera di Luce" (Ball of Light - BOL) che irraggiasse la coltura sottostante.
Per dare maggior consistenza alla sua ipotesi Haselhoff riportò, come controprova, i risultati di uno studio condotto su una formazione di sicura origine umana, comparsa a Nieuwerkerk nel 1997, nella quale lo stesso andamento quadratico non sembrava evidente.
L'ipotesi BOL consiste in un modello che descrive la diminuzione, con il crescere della distanza, dell'intensità di un fronte d'onda sferico di radiazione elettromagnetica originato da una sorgente puntiforme posta ad un'altezza finita h sopra il campo (fig. 1).
Sebbene non esplicitamente indicata nel testo dell'articolo di Haselhoff, l'equazione del modello può essere dedotta da semplici considerazioni fisiche, assumendo una decrescita 1/r2 dell'intensità della radiazione moltiplicato per una costante di proporzionalità, secondo la relazione:
NL - N0 = b/r2
dove b è la costante di proporzionalità e r2 = d2 + h2, dove d è la distanza proiettata al suolo del punto dal centro del cerchio e h l'altezza dell'ipotetica sorgente dal centro del cerchio. Per ogni formazione il parametro h fu ottimizzato per regredire al meglio i dati secondo l'andamento 1/r2. Riscalando l'asse delle x secondo 1/r2 e scegliendo NL-N0 come ordinate, se l'ipotesi BOL fosse corretta ci si dovrebbe attendere un elevato valore del coefficiente di correlazione R2.
Discussione
Sia per i sensazionali contenuti scientifici, sia per lo straordinario impatto esercitato sulla pubblica opinione, sembra necessaria un'analisi più dettagliata sul trattamento dei dati e sull'analisi statistica, in base alla regola che affermazioni straordinarie richiedono prove altrettanto straordinarie.
Prima di iniziare la trattazione riteniamo importante evidenziare come i tre articoli sopra menzionati siano di fatto considerati il "punto di riferimento scientifico" per la comunità delle persone interessate al fenomeno dei crop circles. Physiologia Plantarum Journal giocò un ruolo cruciale, pubblicando tutti e tre gli articoli e fornendo agli autori supporto e credibilità scientifica. Inoltre, il nostro articolo fu dapprincipio sottoposto a Physiologia Plantarum Journal e l'editore si dichiarò d'accordo con i nostri commenti sulla pseudoscientificità dei contenuti dei tre articoli (Physiologia Plantarum Journal, comunicazione agli autori, 2004), ma rifiutò la pubblicazione del nostro articolo con la sorprendente motivazione secondo la quale "non c'è alcun dibattito scientifico in atto su questo argomento".
La nostra prima critica all'articolo di Haselhoff riguarda la strategia di campionamento e l'approccio statistico. Sia il numero di formazioni esaminate, sia il numero di dati raccolti all'interno e all'esterno di ciascuna di esse sono inadeguati per eseguire un'analisi statistica attendibile .
È significativo osservare (vedi Tab.1) come, nel suo articolo del 2001 su Physiologia Plantarum, non sia riportato il numero di campioni raccolti nei vari siti. Omissione piuttosto sorprendente, considerato che la maggior parte delle pubblicazioni scientifiche indica la dimensione della popolazione campionata, in modo da poter dimostrare che le conclusioni statistiche a cui giungono non si fondano su un insieme di pochi dati. Questa è una considerazione importante, perché l'articolo di Haselhoff su Physiologia Plantarum del 2001 sostiene chiaramente che il fenomeno che essi dichiarano di aver scoperto si applica a molti cerchi, non a pochi. Nel caso della formazione di Chehalis, per esempio, i campioni sono stati raccolti solo in tre posizioni e non stupisce che un modello a due parametri possa fornire una regressione apparentemente buona per tre punti, sebbene ciò non indichi una relazione causa-effetto.
| Devizes | Chehalis | Sussex | |||
| d (m) | Nl (mm) | d (m) | Nl (mm) | d (m) | Nl (mm) |
| 0.303 | 6.0 | 1.110 | 4.1c | 0.315 | 4.6c |
| 1.510 | 4.4 | 1.825 | 3.7 | 1.558 | 3.5 |
| 1.529 | 5.5 | 4.543 | 3.5 | 4.476 | 3.3 |
| 2.812 | 4.4 | 9.109 | 3.3 | 4.830 | 3.4 |
| 2.897 | 4.3 | 12.224 | 2.8e | ||
| 3.300 | 3.3e | 19.775 | 2.4e | ||
| controllo | 3.2 | controllo | 2.9 | controllo | 2.4 |
La BOL è un modello di regressione a due parametri: l'altezza h dal suolo e la costante di proporzionalità b. Il parametro b non è così insignificante da meritare di essere superficialmente trascurato, come è stato fatto nell'articolo di Haselhoff, ma dovrebbe giocare un ruolo cruciale nel processo fisico sottostante. In realtà il parametro b contiene tutte le informazioni non geometriche del fenomeno. Piuttosto che una costante esso rappresenta, in effetti, un insieme di più variabili. Esso descrive tutte le proprietà fisiche del fenomeno come, per esempio, la durata dell'irraggiamento, l'intervallo spettrale della radiazione emessa, l'intensità della sorgente, l'assorbimento dell'aria, il contenuto di umidità delle piante e del suolo circostante, le proprietà assorbenti e riflettenti delle piante e del suolo e così via.
Per le formazioni di Devizes e Chehalis, entrambe all'interno di coltivazioni di frumento, abbiamo trovato rispettivamente b=10,3 e b=68,9; si tratta di valori ben diversi. Haselhoff non solo ha omesso di spiegare il significato dei parametri e la ragione delle loro differenze, ma ne ha omesso anche la pubblicazione dei valori. In particolare, solo l'altezza h della BOL dal suolo è riportata nella tabella 1 dell'articolo di Haselhoff. Ne segue che il modello sembra possedere un solo parametro, l'altezza h, fornendo dei risultati sorprendentemente buoni per un modello a un solo parametro.
Un altro aspetto criticabile riguarda la mancanza di un protocollo standardizzato per stabilire quali misure includere nel gruppo di controllo. Alcune piante rimaste erette molto lontano dalle formazioni furono definite come "controlli" e considerate come piante indisturbate; i loro valori medi e le deviazioni standard furono calcolate in modo da permettere il paragone tra piante affette e piante non affette. Le piante appiattite all'interno dei cerchi furono considerate "affette" (cioè non-controlli). In realtà, anche alcune piante erette, raccolte all'esterno dei cerchi, furono considerate "affette" e non classificate nel gruppo di controllo: due campioni nella formazione del Sussex furono raccolti a 6 e 14 metri dal limite esterno del cerchio e un campione a Devizes fu raccolto 30 centimetri oltre il bordo della formazione (figure 2a e 2c). Nessuna giustificazione relativamente a questa decisione è stata addotta nell'articolo. Nessuna distanza limite per l'inclusione o meno dei campioni nei gruppi di controllo è menzionata. Dobbiamo supporre che gli autori abbiano deciso di assegnare queste piante al gruppo delle "affette" piuttosto che a quello dei controlli dopo aver osservato che i loro allungamenti erano maggiori di quelli delle piante definite "controllo". Questa è una procedura che può generare artefatti.
Ci potrebbero essere delle ragioni per includere alcune piante rimaste erette all'esterno dei cerchi nel gruppo delle piante "affette", dato che gli autori sembrano indagare su effetti che potrebbero non essere strettamente limitati all'area del raccolto abbattuto al suolo. Tuttavia, se nessun criterio oggettivo viene stabilito chiaramente e a priori, ogni analisi successiva diventa discutibile, perché la deviazione standard dei controlli può essere sottostimata, rendendo i valori degli allungamenti dei nodi delle piante "affette" apparentemente più anomali di quanto essi siano.
Inoltre, se il bordo del cerchio non è assunto come criterio discriminante, diventa più complicato assicurarsi che gli effetti che si stanno investigando siano realmente provocati dal fenomeno che ha generato il cerchio, piuttosto che da altre cause concorrenti. Questo è particolarmente rilevante se si considera che, a causa dello scarso numero di campioni raccolti, l'analisi manca di risoluzione spaziale e che le piante di controllo sono state raccolte solo a grandi distanze dal bordo dei cerchi, dove le condizioni ambientali potrebbero essere state un po' diverse. Nessun test statistico per confrontare le medie e le varianze dei campioni presi all'interno e all'esterno delle formazioni è stato applicato. Qualsiasi conclusione fondata sul paragone fra campioni raccolti all'interno dei cerchi e quelli provenienti dal resto del raccolto non è, quindi, supportata da un'analisi statistica robusta.
La figura 2 mostra le misure effettuate nelle tre formazioni di Devizes (a), Chehalis (b) e Sussex (c). I raggi dei tre cerchi furono rispettivamente di 3, 6 e 9 metri e tutte le piante rimaste erette all'esterno avrebbero dovuto essere considerate come campioni di controllo, a meno che non venisse dichiarato un diverso criterio.

Figura 2. Paragone fra il modello BOL (linea tratteggiata) ed una semplice regressione lineare (linea continua) per le formazioni: (a) Devizes, (b) Chehalis, (c) Sussex e (d) Nieuwerkerk. I ciuffi centrali sono inclusi nell'analisi. I quadrati vuoti indicano i ciuffi centrali; i cerchi vuoti rappresentano le piante raccolte all'esterno delle formazioni.
Ciò nonostante, il primo punto a destra nel grafico di Devizes e i primi due in quello del Sussex furono inclusi nel modello di regressione sia da Levengood e Talbott che da Haselhoff, nonostante la loro reale natura di controlli. Particolarmente sorprendente è il caso del Sussex, in cui l'intervallo di confidenza del gruppo di controllo è molto piccolo mentre uno dei campioni (controllo) si trova ben al di fuori di esso. Chiaramente questo punto fu escluso dal calcolo della deviazione standard dei livelli di controllo, conducendo a una sottostima del reale valore e rendendo, quindi, impossibile un confronto attendibile fra la variabilità degli allungamenti dei nodi delle piante interne al cerchio e di quelle appartenenti al resto della coltivazione.
Nelle formazioni del Sussex e di Chehalis furono rinvenuti ciuffi circolari di piante rimaste erette al centro dei cerchi, eppure questi campioni furono esclusi dall'analisi della regressione del modello, nonostante si trovassero nel cuore dei cerchi e nonostante l'importanza di questi campioni vista la loro prossimità alla presunta sorgente radiante. Levengood e Talbott esclusero il ciuffo centrale sebbene, grazie all'omissione del fattore di dispersione dell'energia, questo non costituisse alcuna singolarità per il loro modello esponenziale. Sebbene Haselhoff possa aver escluso i ciuffi centrali con l'obiettivo di confrontare i propri risultati con quelli di Levengood e Talbott, egli avrebbe dovuto includerli al fine di valutare correttamente le prestazioni del suo modello.
Inoltre critichiamo la mancanza di informazioni sulla significatività statistica dei parametri del modello proposto. Questo tipo di valutazione è imprescindibile perché permette di giudicare l'attendibilità della regressione, basata sulla trasformazione dell'asse x in seguito all'ottimizzazione del parametro h. Ripetendo le analisi di regressione di Haselhoff sui dati originali, abbiamo scoperto che il parametro h non è significativo al livello a=0,05 (tabella 2a), che costituisce già un limite piuttosto generoso per un'affermazione tanto clamorosa. Includendo i ciuffi centrali nei dati, peggiorano sia i coefficienti di correlazione R2 sia la significatività statistica di h (tabella 2a); pertanto, il modello BOL appare statisticamente privo di attendibilità o, perlomeno, non sufficientemente significativo da ritenere ragionevole l'esistenza di una sorgente puntiforme di radiazione elettromagnetica che irraggi dall'alto i cerchi nel grano.

Tabella 2a. Parametri del modello BOL, applicato ai dati di Chehalis, Sussex e Devizes. Il parametro h è l'altezza dal suolo della sorgente radiante puntiforme, R2 è il coefficiente di correlazione, p è la probabilità che il valore effettivo del parametro h sia zero anziché il valore indicato. I risultati di Haselhoff furono ottenuti escludendo i ciuffi centrali di piante erette. Sia escludendo che includendo i ciuffi centrali nel calcolo, i parametri del modello BOL non sono statisticamente significativi al 95% di confidenza (il valore p è maggiore di 0,05). Devizes non è stato preso in considerazione perché mancante di ciuffi centrali.
Va sottolineato come una semplice regressione lineare, che ha lo stesso numero di parametri, approssimi i dati meglio di quanto faccia il modello BOL (tabella 2b). Naturalmente, non stiamo suggerendo l'esistenza di uno specifico sottostante fenomeno lineare, ma vogliamo semplicemente mettere in luce un concetto basilare: l'esistenza di una correlazione non è necessariamente indice di un nesso di causalità. In aggiunta, è molto importate sottolineare che l'applicazione di test statistici a un numero così scarso di dati può condurre a conclusioni errate che sono ben lungi dall'essere statisticamente significative.

Tabella 2b. Parametri del modello di regressione lineare applicato ai dati di Chehalis, Sussex e Devizes. Il parametro h è l'altezza dal suolo della sorgente radiante puntiforme, R2 è il coefficiente di regressione lineare e a è il parametro di pendenza. Una semplice regressione lineare interpola tutti i dati con maggiore significatività statistica; nel caso senza ciuffi centrali considerato da Haselhoff, li approssima anche meglio.
Il modello BOL, inoltre, è irrealistico anche da un punto di vista fisico. Un ipotetico modello BOL dovrebbe essere molto più complesso, perché la quantità di energia che colpisce le piante dovrebbe dipendere dall'angolo di incidenza della radiazione rispetto ai nodi degli steli e l'assorbimento di energia dipenderebbe dal cammino percorso dalla radiazione all'interno delle piante e, di conseguenza, dalla loro effettiva trasparenza. Uno stelo parzialmente trasparente schermerebbe in parte il nodo; ne conseguirebbe che il modello di Haselhoff potrebbe funzionare solo assumendo che le piante fossero del tutto trasparenti alla radiazione e pertanto non potrebbero assorbire alcuna energia. Quindi, se ci fosse davvero una sorgente puntiforme ad irraggiare i raccolti, la sua impronta non mostrerebbe comunque un andamento 1/r2.
Abbiamo ottenuto da Haselhoff (Haselhoff, comunicazione agli autori, 2003) le misure originali raccolte nella formazione di origine umana di Nieuwerkerk (fig. 3) e le abbiamo confrontate con quanto riportato nell'articolo di Haselhoff.

Figura 3.
Rappresentazione schematica delle formazioni di conclamata origine umana di Nieuwerkerk. Il cerchio in grigio chiaro è quello campionato. In alto a destra, un ingrandimento del cerchio campionato e l'indicazione delle posizioni di misura. Entrambi i set A e B sono stati raccolti da Haselhoff, ma solo il set A è stato pubblicato. Il set B non è riportato nell'articolo di Haselhoff.
Rappresentazione schematica delle formazioni di conclamata origine umana di Nieuwerkerk. Il cerchio in grigio chiaro è quello campionato. In alto a destra, un ingrandimento del cerchio campionato e l'indicazione delle posizioni di misura. Entrambi i set A e B sono stati raccolti da Haselhoff, ma solo il set A è stato pubblicato. Il set B non è riportato nell'articolo di Haselhoff.
La prima cosa che osservammo fu che gli allungamenti dei nodi arrivavano sino al 30%, contraddicendo le conclusioni dell'esperimento di Levengood e Talbott nel Maryland (1997), in cui si stimò che il gravitropismo ammontasse a non più del 10%, e dimostrando nel contempo che piante prelevate in formazioni di dichiarata origine umana potevano presentare allungamenti confrontabili con quelli di piante raccolte in formazioni considerate non antropogeniche ("genuine").
Esaminando il caso di Nieuwerkerk, inoltre, notammo che questa volta il primo punto esterno al cerchio era stato escluso dall'analisi, nonostante distasse appena 10 centimetri dal bordo del cerchio (cioè 12,8 metri dal centro). Includendo questo punto nella regressione, come necessario per eseguire un confronto coerente con le analisi eseguite sulle altre formazioni "genuine", il coefficiente di correlazione del modello BOL cambia da R=0,54 a R=0,63.
La cosa più sorprendente, tuttavia, fu scoprire che solo una parte delle misure sperimentali era stata pubblicata nell'articolo. Durante l'esperimento, Haselhoff raccolse due serie di misure, chiamate set A e set B, raccogliendo i campioni secondo due direttrici perpendicolari fra loro sulla stessa impronta circolare, ma pubblicò i risultati del solo set A. Il coefficiente di correlazione del modello BOL applicato al set B è R=0,71, decisamente più alto di quello del set A.
Usando entrambi i set, mediando i valori dei punti che si trovavano all'interno del cerchio, alla stessa distanza dal centro (fig. 2d), trovammo che il coefficiente di correlazione per il modello BOL cresce a R=0,73. Inoltre, includendo tutti i dati disponibili appartenenti alla parte esterna dei cerchi e usando come valore di controllo la media di tutti i punti esterni, il coefficiente di correlazione sale a R=0,83. In conclusione: piante raccolte in formazioni di dichiarata origine umana possono rivelare proprietà statistiche simili a quelle di formazioni considerate "genuine".
Un'altra critica riguarda la mancanza di analisi della formazione a spirale di Beckhampton, sebbene questo esperimento fosse stato dettagliatamente descritto nell'articolo di Levengood e Talbott, lo stesso articolo commentato da Haselhoff. In realtà, la formazione di Beckhampton non presenta alcun andamento 1/r2; gli allungamenti dei nodi non sembrano neppure correlati con la distanza dal centro. Ricordiamo che tutti gli esperimenti devono essere presi in considerazione e che una teoria è valida solo quando è in grado di spiegare tutti i casi e non solo quelli che si accordano con l'ipotesi sperimentale.
Si potrebbe ipotizzare che, per riuscire a tracciare una spirale nel raccolto, una BOL avrebbe dovuto muoversi in modo complesso piuttosto che stazionare semplicemente sopra il centro; questo movimento complesso impedirebbe di scorgere nei dati l'andamento 1/r2, rendendo chiare le ragioni dell'esclusione dall'analisi.
Tuttavia, questa giustificazione condurrebbe a porsi domande circa la portata dei tre articoli. È normalmente accettato dai "credenti" che i cerchi nel grano siano opera di esseri senzienti, perché (presumibilmente) i fenomeni naturali non sarebbero in grado di generare una tale varietà di figure geometriche dall'apparenza così simbolica. Queste avvincenti proprietà geometriche non sono però presenti nelle semplici forme circolari o in quelle irregolari (non-geometriche). Se una pubblicazione scientifica si focalizza solo sui semplici cerchi, le sue conclusioni non possono poi essere estese alle formazioni complesse se non affidandosi alla discutibile implicita assunzione che possa esistere una sola unica causa per l'abbattimento delle piante. Se un articolo scientifico non prende in considerazione anche le formazioni complesse allora la sua rilevanza nei confronti di ciò che la gente chiama "cerchi nel grano" rimane tutta da dimostrare.
Un'altra critica fondamentale riguarda l'inconsistenza delle assunzioni. Nell'articolo di Levengood e Talbott è suggerito che l'allungamento dei nodi sia dovuto ad un rapido e intenso riscaldamento dei tessuti delle piante, conseguente all'assorbimento di radiazione elettromagnetica. Il riscaldamento dell'acqua contenuta nelle cellule sarebbe all'origine di un aumento di pressione interna che, a sua volta, forzerebbe i tessuti visco-elastici ad allungarsi. Nel suo articolo, pubblicato nel 1994, Levengood sostenne che "se energia da microonde è coinvolta nella formazione dei crop circles, la quantità di calore dovrebbe dipendere dal contenuto d'acqua della pianta". La dilatazione termica dell'acqua liquida fra 15 °C e 90 °C, tuttavia, è non più del 3,5%, non sufficiente a giustificare gli allungamenti tra il 30% e il 200% osservati per i nodi nelle formazioni (Levengood & Talbott, 1999).
Inoltre, sia Levengood e Talbott (1999) che J.A. Burke (1998), un membro dello stesso gruppo di ricerca (BLT), affermarono che danni alle piante (allungamenti dei nodi) di maggior entità si rinvengono in piante abbattute al suolo a causa del vento o di condizioni meteorologiche severe.
Tutte le ipotesi formulate attorno alla creazione dei cerchi si fondano su un effetto termomeccanico, ma nessuno degli autori ha mai dimostrato la possibilità per i nodi di potersi allungare sino del 200% o anche del 100%, così come osservato nelle formazioni "genuine", sotto l'azione di un riscaldamento. Eppure non sembra difficile verificare se i nodi possano effettivamente allungarsi sotto l'azione di calore radiante (senza bruciare o uccidere le piante); ma finché una qualche evidenza di laboratorio per l'effetto termomeccanico non viene prodotta, allungamenti dei nodi come quelli dichiaratamente osservati nei cerchi nel grano non possono essere collegati all'assorbimento di una qualche forma di irraggiamento elettromagnetico.
Un'altra critica riguarda la mancanza di informazioni dettagliate su ogni argomento trattato negli articoli: nessuna fotografia delle tre formazioni genuine, né del "falso" di Nieuwerkerk è stata prodotta; nessuna tabella con i dati originali è stata riportata; non è stata fornita alcuna descrizione sulla geometria dell'appiattimento delle piante (cioè nulla è stato detto sulla posizione delle piante abbattute); nulla è stato scritto sulla posizione in cui i campioni sono stati raccolti all'interno del cerchio, tranne la loro distanza dal centro. Quindi lo studio non permette un'analisi bidimensionale; nessuna incertezza sul valore delle ascisse è riportata, laddove ogni punto di campionamento rappresentava in effetti la lunghezza media dei nodi di circa 10-15 piante e piccole differenze nella distanza dal centro producono enormi variazioni nell'allungamento dei nodi, come nel caso della formazione di Devizes in cui il secondo e terzo punto distavano solo 1,9 cm eppure gli allungamenti differiscono addirittura dell'86%. Nessuna ipotesi è stata formulata su ciò che riguarda la durata, l'intensità e la frequenza della presunta radiazione. Infine, l'opacità delle piante alla radiazione, che implica la necessità di considerazioni sugli angoli di incidenza, può drammaticamente modificare la simmetria del meccanismo di assorbimento di energia e, quindi, l'equazione del modello; questo elemento è stato del tutto ignorato.
Conclusioni
La nostra conclusione è che le affermazioni sul coinvolgimento di una qualche forma di irraggiamento elettromagnetico all'origine della formazione dei cerchi nel grano non trova supporto nell'evidenza sperimentale. In particolare, l'andamento 1/r2 esiste solo in virtù di un'esclusione ingiustificata di dati indesiderati; nonostante ciò, anche in queste condizioni privilegiate, il modello proposto non interpola i dati altrettanto bene quanto una semplice regressione lineare. E seppure un andamento 1/r2 fosse evidenziabile nei dati sperimentali, esso non potrebbe comunque essere attribuito ad una sorgente puntiforme di radiazione, perché implicherebbe la completa trasparenza delle piante rispetto alla radiazione incidente, impedendo qualunque assorbimento di energia. Inoltre, il modello BOL è stato selettivamente applicato alle sole formazioni dalla struttura circolare semplice, laddove le forme rettangolari o più complesse sono state deliberatamente ignorate per l'impossibilità di adattarle all'ipotesi BOL.
I fatti discussi nel nostro articolo critico non dimostrano nient'altro che l'esistenza di una semplice differenza nell'allungamento dei nodi delle piante abbattute all'interno dei cerchi rispetto a quelle rimaste erette al loro esterno, come ci si dovrebbe attendere nel caso in cui un qualunque tipo di azione meccanica riuscisse ad appiattire al suolo le piante, corde e assi comprese.
Bibliografia
- Levengood, W.C. & Talbott, N.P. (1999), "Dispersion of
- Haselhoff, E.H. (2001), "Opinions and comments on Levengood
- Levengood, W.C. (1994), "Anatomical anomalies in crop
Francesco Grassi
Ingegnere,
Gruppo sperimentazioni CICAP
Claudio Cocheo
Centro di Ricerche Ambientali,
Fondazione Salvatore Maugeri, CICAP Veneto
Paolo Russo
Programmatore, CICAP Friuli Venezia Giulia
Tutti e tre fanno parte del Gruppo di Ricerca del CICAP sui Crop Circles Traduzione italiana a cura di Claudio Cocheo pubblicata su Scienza & Paranormale (S&P N. 63 - Anno XIII -Set/Ott 2005) dell'articolo originale in inglese pubblicato su Journal of Scientific Exploration Vol. 19, n.2, pp. 159-170, 2005 (PDF version)