Tra le figure cariche di stereotipi, certamente rientra quella degli scienziati. Fra tutti, il genio matematico è quello a cui si riferiscono più luoghi comuni: il matematico è maschio, scontroso, bizzarro, molto spesso ha i capelli (bianchi) arruffati.
Anche la rappresentazione dell’artista abbonda di luoghi comuni. Fra i più radicati si trova la sregolatezza di vita, l’irrazionalità, l’incostanza e le vicende sentimentali tormentate.
Malgrado l’esistenza di numerose e lodevoli eccezioni, si tratta di “topoi” frequentemente confermati e diffusi da film che narrano, in modo romanzato, la vita di noti artisti o scienziati. Queste due figure, il matematico e l’artista, sembrerebbero non avere alcun punto in comune (eccetto, in qualche caso, i capelli arruffati). Logico e razionale il primo, istintivo e mutabile il secondo. L’uno immerso nella razionalità delle proprie ricerche, l’altro ispirato e sognante.
Alcuni luoghi comuni germogliano in determinate epoche, e cominciano a manifestarsi con la settorializzazione delle scienze. Quelli descritti sopra sono relativamente recenti e probabilmente risalgono al periodo romantico. Si cristallizzano successivamente nel corso del rapido sviluppo delle scienze e della tecnologia, e soprattutto con il consolidarsi dello sviluppo industriale.
I capelli bianchi arruffati, è evidente, sono quelli di Einstein, nel XX secolo.
Non è stato però così in ogni epoca.
La passione per l’arte e per la scienza sono andate di pari passo e per lungo tempo non sono state considerate inconciliabili. Per tenere traccia di un loro diverso e armonioso rapporto possiamo affidarci a un inaspettato alleato: la musica. Suona infatti il violino Sherlock Holmes, emblema di razionalità per il suo creatore, Conan Doyle; coltiva la passione per il violino Einstein, il genio per eccellenza.
Proprio il violino può far da guida in un percorso alla riscoperta del legame fra arte e scienza. Trascuriamo per un momento gli stuoli di immaginari violinisti celati tra le fronde o le cortine durante le scene romantiche dei film. Accantoniamo per un attimo gli slanci lirici dei “violini zigani”.
Vediamo invece come il violino possa costituire un’importante fonte di ispirazione per la ricerca scientifica, incluse matematica e fisica.
Il violino (Fig. 1) suona attraverso lo strofinamento delle corde, che vibrando producono onde di rarefazione e compressione nell’aria, amplificate dalla cassa armonica. Pressando le dita della mano sinistra sulle corde in determinate porzioni di lunghezza, e strofinando o pizzicando le corde, si ottengono suoni di diversa altezza.
Questo, già nel 500 a.C., è compreso da Pitagora, il quale non inventa il violino, ma un suo antenato, il monocordo, che presenta, appunto, una sola corda. Gli antichi Greci conoscono la cetra e la lira; gli antichi Egizi e altre culture conoscono l’arpa (Fig. 2); i Persiani l’oud, una sorta di liuto; i Cinesi l’ehru.
L’intuizione del nesso fra matematica e suoni risale proprio all’epoca dei Greci, e dà il via, in Occidente, allo sviluppo contemporaneo di entrambi gli ambiti. (In Cina un simile effetto è ascrivibile a Zaiyu Zhu, il Pitagora cinese). Si deve tuttavia attendere il Rinascimento per vedere apparire in Italia la viola da gamba e la viola da braccio, e poi i primi esemplari di violino, viola e violoncello e del contrabbasso.
Due nomi che esemplificano lo stretto intreccio esistente fra arti e scienze in un passato non molto remoto sono quelli di Tartini e di Eulero, entrambi vissuti nel 1700.
Giuseppe Tartini è un violinista triestino, compositore e teorico della musica, che diviene un importante studioso di acustica. Ha degli scambi epistolari con Eulero[1], uno dei più grandi matematici di tutti i tempi. Tartini scopre uno strano fenomeno: dalla sovrapposizione di due suoni, se ne emette un terzo, avente, per frequenza, la differenza delle frequenze dei suoni originari: il “terzo suono di Tartini”. In alcuni casi il suono risultante è molto evidente. Nel 1754 Tartini pubblica il “Trattato di musica secondo la vera scienza dell’Armonia”[2]. In realtà, oltre al terzo suono, se ne emette anche un altro, più debole, avente per frequenza la semisomma della frequenze dei suoni originari.
Eulero (Leonhard Euler), uno dei matematici scientificamente più prolifici della storia, contribuisce a tutta la scienza matematica e rivela anche un profondo interesse per la musica. Eulero studia il “gradus suavitatis” degli intervalli musicali e definisce la “Tonnetz”, un reticolato per descrivere in astratto i rapporti fra note e accordi. Definisce anche uno spazio geometrico per le note, lo “spazio di Eulero”, dove l’asse x indica gli intervalli di quinta, l’asse y le terze maggiori e l’asse z le ottave.
Dal punto di vista prettamente matematico, al centro della ricerca di Eulero si trovano l’Analisi Infinitesimale e la Meccanica Razionale. Eulero è il principale creatore dal Calcolo delle variazioni e delle equazioni differenziali, nonché un precursore della Geometria differenziale delle superfici. Ma non si limita a questi risultati: fonda la meccanica del continuo, approfondisce gli studi sulla balistica, la cartografia, la teoria dell’elasticità, l’idraulica, l’idrodinamica, la teoria dei numeri, l’ottica, la diottrica e la teoria della nave. E, naturalmente, anche gli studi sulla teoria della musica. La sua dissertazione si intitola “De Sono”; uno dei suoi libri “Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae”.
In pieno Ottocento è un matematico (e fotografo) l’autore di “Alice nel Paese delle Meraviglie”, Lewis Carroll. In tempi più recenti, troviamo il violinista e matematico Wolfgang Graeser (1906-1928), uno studioso svizzero-tedesco che trascorre l’infanzia a Napoli. Graeser si dedica al disegno e alla pittura, studia latino, greco, cinese, sanscrito, ed è inoltre un atleta. Nella sua breve vita, Graeser si occupa anche di musicologia. Riscopre l’Arte della Fuga di Bach, descrive le note come punti in uno spazio geometrico, sviluppa una visione del contrappunto basata su simmetrie locali fuse insieme per creare strutture globali, sfruttando il concetto di insiemi dentro insiemi dentro insiemi (annidati). Graeser intuisce inoltre una connessione profonda fra la danza, la musica, l’atletica, il pensiero simbolico e la sua attuazione corporea[3],[4].
Ai nostri giorni, fra le donne che si occupano di matematica e musica citiamo la pianista e concertista Eugenia Cheng, matematico, specialista nella teoria delle categorie. Ha insegnato per anni a Cambridge e ora si dedica alla divulgazione. Violinista e matematica è pure Lillian Beatrix Pierce (Sadosky Prize 2018). Lillian Pierce (Fig. 3) si dedica alla teoria dei numeri e alle funzioni armoniche. Queste ultime soddisfano un’equazione con un operatore (di Laplace) presente anche nell’equazione delle onde sonore. Non è proprio un caso che la parola “armonico” rimandi alla musica e allo studio degli accordi, ossia all’“armonia”. In un’intervista5 del 2014, Pierce dichiara di applicare alla matematica molte delle abilità mentali apprese come musicista. In una sua affermazione[5], cita il “focus e la dedizione e l’immaginario mentale necessario per memorizzare un brano musicale e visualizzare come funziona — io abito lo stesso spazio mentale anche quando faccio matematica”.
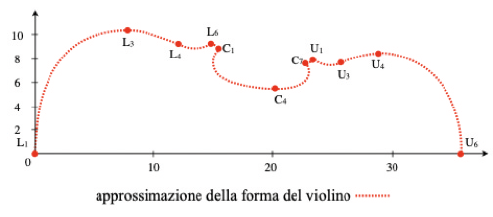
Potrebbe essere la forma stessa del violino a ispirare studi matematici. La forma dello strumento si può infatti schematizzare per mezzo di particolari equazioni parametriche cubiche, dette “cubic parametric splines”. Una “spline” è costituita da polinomi raccordati fra loro (come funzioni “definite a tratti”). Il matematico e violoncellista Roel Stroeker[6], dopo la pensione, inizia a studiare la costruzione degli strumenti ad arco e crea un modello della forma del violino (Figure 4 e 5).
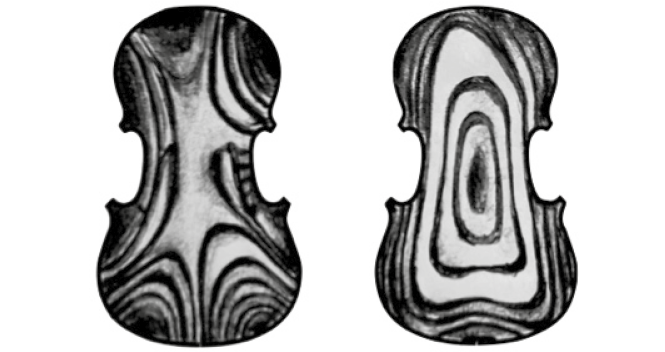
Se le corde (approssimiamole come 1-dimensionali) oscillano, oscillano anche le tavole armoniche (approssimiamole come 2-dimensionali). I “modi normali di oscillazione” della tavola armonica del violino mostrano figure simmetriche o asimmetriche, che si possono rilevare anche tramite l’interferometria[7] (Fig. 6). Questi studi aiutano a costruire strumenti dal suono ancora più bello.
Quale potrebbe essere la vera causa del distacco fra il mondo artistico e il mondo scientifico, e perché tale distacco viene oggi considerato un problema? In fondo si potrebbe accettare l’ipotesi che il naturale sviluppo delle discipline scientifiche conduca necessariamente alla specializzazione e quindi a un allontanamento perfino tra discipline affini. Se oggi un matematico e un astrofisico hanno difficoltà a raccontarsi l’un l’altro le proprie ricerche più avanzate, perché stupirsi che ciò accada tra la scienza e l’arte? Eppure, gli esempi presentati in precedenza, seppure limitati alla musica, mostrano quanto sia ancora vivo questo legame.
È probabile che il problema risieda nella percezione sociale di queste discipline. Ne soffrono un po’ in tutto il mondo, in particolare, le discipline scientifiche. Tanti studenti, sin dai primi anni della scuola secondaria, si allontanano dallo studio della scienza perché percepita come troppo difficile, fredda, utilitaristica e slegata da altri aspetti come, per esempio, la bellezza. È ancora troppo basso il numero di studentesse che si iscrivono alle facoltà scientifiche malgrado i brillanti risultati conseguiti in queste materie nella scuola secondaria. Nonostante la notevole considerazione per le scienze, troppi studenti se ne allontanano precocemente, un fenomeno ancora più evidente in categorie sociali a rischio.
È anche per questi motivi che continua a farsi strada l’idea di affiancare all’insegnamento delle discipline STEM (Science, Technology, Engineering, Mathematics) l’insegnamento delle arti. Si comincia a parlare sempre più di STEAM, ritenendo necessario l’inserimento della “A” di Arte per modificare la percezione delle discipline scientifiche e renderle più inclusive.
Le stesse osservazioni valgono in modo speculare. In un’intervista concessa alla televisione svizzera negli anni ‘70, il grande scrittore Gianni Rodari, alla domanda: “Cosa si deve fare per diventare scrittori?”, risponde in modo apparentemente provocatorio, in realtà lungimirante: “Studiare matematica”[8].
Sarebbe il caso di trarre spunto dalla tradizione greca per individuare e valorizzare ciò che può apparire un paradosso: gli aspetti scientifici dell’arte e gli aspetti artistici della scienza.
E chissà se i violinisti nascosti nelle scene romantiche dei film non aggiungano alla chimica dei momenti sentimentali... un po’ di matematica.
Anche la rappresentazione dell’artista abbonda di luoghi comuni. Fra i più radicati si trova la sregolatezza di vita, l’irrazionalità, l’incostanza e le vicende sentimentali tormentate.
Malgrado l’esistenza di numerose e lodevoli eccezioni, si tratta di “topoi” frequentemente confermati e diffusi da film che narrano, in modo romanzato, la vita di noti artisti o scienziati. Queste due figure, il matematico e l’artista, sembrerebbero non avere alcun punto in comune (eccetto, in qualche caso, i capelli arruffati). Logico e razionale il primo, istintivo e mutabile il secondo. L’uno immerso nella razionalità delle proprie ricerche, l’altro ispirato e sognante.
Alcuni luoghi comuni germogliano in determinate epoche, e cominciano a manifestarsi con la settorializzazione delle scienze. Quelli descritti sopra sono relativamente recenti e probabilmente risalgono al periodo romantico. Si cristallizzano successivamente nel corso del rapido sviluppo delle scienze e della tecnologia, e soprattutto con il consolidarsi dello sviluppo industriale.
I capelli bianchi arruffati, è evidente, sono quelli di Einstein, nel XX secolo.
Non è stato però così in ogni epoca.
La passione per l’arte e per la scienza sono andate di pari passo e per lungo tempo non sono state considerate inconciliabili. Per tenere traccia di un loro diverso e armonioso rapporto possiamo affidarci a un inaspettato alleato: la musica. Suona infatti il violino Sherlock Holmes, emblema di razionalità per il suo creatore, Conan Doyle; coltiva la passione per il violino Einstein, il genio per eccellenza.
Contro gli stereotipi
Proprio il violino può far da guida in un percorso alla riscoperta del legame fra arte e scienza. Trascuriamo per un momento gli stuoli di immaginari violinisti celati tra le fronde o le cortine durante le scene romantiche dei film. Accantoniamo per un attimo gli slanci lirici dei “violini zigani”.
Vediamo invece come il violino possa costituire un’importante fonte di ispirazione per la ricerca scientifica, incluse matematica e fisica.
Figura 2. Arpista da un altorilievo proveniente da Butkara, Pakistan, primo secolo d.C. Museo Nazionale d’Arte Orientale, Roma. Disegno di M. M.
Questo, già nel 500 a.C., è compreso da Pitagora, il quale non inventa il violino, ma un suo antenato, il monocordo, che presenta, appunto, una sola corda. Gli antichi Greci conoscono la cetra e la lira; gli antichi Egizi e altre culture conoscono l’arpa (Fig. 2); i Persiani l’oud, una sorta di liuto; i Cinesi l’ehru.
L’intuizione del nesso fra matematica e suoni risale proprio all’epoca dei Greci, e dà il via, in Occidente, allo sviluppo contemporaneo di entrambi gli ambiti. (In Cina un simile effetto è ascrivibile a Zaiyu Zhu, il Pitagora cinese). Si deve tuttavia attendere il Rinascimento per vedere apparire in Italia la viola da gamba e la viola da braccio, e poi i primi esemplari di violino, viola e violoncello e del contrabbasso.
Due nomi che esemplificano lo stretto intreccio esistente fra arti e scienze in un passato non molto remoto sono quelli di Tartini e di Eulero, entrambi vissuti nel 1700.
Giuseppe Tartini è un violinista triestino, compositore e teorico della musica, che diviene un importante studioso di acustica. Ha degli scambi epistolari con Eulero[1], uno dei più grandi matematici di tutti i tempi. Tartini scopre uno strano fenomeno: dalla sovrapposizione di due suoni, se ne emette un terzo, avente, per frequenza, la differenza delle frequenze dei suoni originari: il “terzo suono di Tartini”. In alcuni casi il suono risultante è molto evidente. Nel 1754 Tartini pubblica il “Trattato di musica secondo la vera scienza dell’Armonia”[2]. In realtà, oltre al terzo suono, se ne emette anche un altro, più debole, avente per frequenza la semisomma della frequenze dei suoni originari.
Eulero (Leonhard Euler), uno dei matematici scientificamente più prolifici della storia, contribuisce a tutta la scienza matematica e rivela anche un profondo interesse per la musica. Eulero studia il “gradus suavitatis” degli intervalli musicali e definisce la “Tonnetz”, un reticolato per descrivere in astratto i rapporti fra note e accordi. Definisce anche uno spazio geometrico per le note, lo “spazio di Eulero”, dove l’asse x indica gli intervalli di quinta, l’asse y le terze maggiori e l’asse z le ottave.
Dal punto di vista prettamente matematico, al centro della ricerca di Eulero si trovano l’Analisi Infinitesimale e la Meccanica Razionale. Eulero è il principale creatore dal Calcolo delle variazioni e delle equazioni differenziali, nonché un precursore della Geometria differenziale delle superfici. Ma non si limita a questi risultati: fonda la meccanica del continuo, approfondisce gli studi sulla balistica, la cartografia, la teoria dell’elasticità, l’idraulica, l’idrodinamica, la teoria dei numeri, l’ottica, la diottrica e la teoria della nave. E, naturalmente, anche gli studi sulla teoria della musica. La sua dissertazione si intitola “De Sono”; uno dei suoi libri “Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae”.
In pieno Ottocento è un matematico (e fotografo) l’autore di “Alice nel Paese delle Meraviglie”, Lewis Carroll. In tempi più recenti, troviamo il violinista e matematico Wolfgang Graeser (1906-1928), uno studioso svizzero-tedesco che trascorre l’infanzia a Napoli. Graeser si dedica al disegno e alla pittura, studia latino, greco, cinese, sanscrito, ed è inoltre un atleta. Nella sua breve vita, Graeser si occupa anche di musicologia. Riscopre l’Arte della Fuga di Bach, descrive le note come punti in uno spazio geometrico, sviluppa una visione del contrappunto basata su simmetrie locali fuse insieme per creare strutture globali, sfruttando il concetto di insiemi dentro insiemi dentro insiemi (annidati). Graeser intuisce inoltre una connessione profonda fra la danza, la musica, l’atletica, il pensiero simbolico e la sua attuazione corporea[3],[4].
Figura 3. Lillian Pierce. Ritratto di M. M.
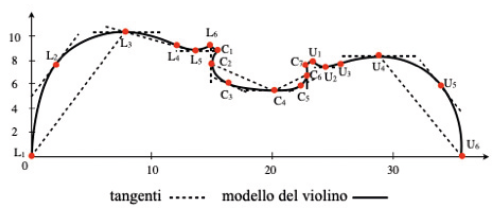
Potrebbe essere la forma stessa del violino a ispirare studi matematici. La forma dello strumento si può infatti schematizzare per mezzo di particolari equazioni parametriche cubiche, dette “cubic parametric splines”. Una “spline” è costituita da polinomi raccordati fra loro (come funzioni “definite a tratti”). Il matematico e violoncellista Roel Stroeker[6], dopo la pensione, inizia a studiare la costruzione degli strumenti ad arco e crea un modello della forma del violino (Figure 4 e 5).
Figura 4. Studio della forma del violino attraverso l’individuazione di punti e delle tangenti ad alcuni punti. Figura di M. M. realizzata a partire dal grafico originale di R. J. Stroeker, fig. 2 in (6).
Figura 5. Approssimazione della forma del violino per pezzo delle splines parametriche e la scelta di 11 punti fra quelli individuati nella figura 4. Immagine originale: figura 5 da (6). Rielaborazione di M. M.
Se le corde (approssimiamole come 1-dimensionali) oscillano, oscillano anche le tavole armoniche (approssimiamole come 2-dimensionali). I “modi normali di oscillazione” della tavola armonica del violino mostrano figure simmetriche o asimmetriche, che si possono rilevare anche tramite l’interferometria[7] (Fig. 6). Questi studi aiutano a costruire strumenti dal suono ancora più bello.
Figura 6. modi di vibrazione di piani armonici del violino per 222 Hz e 348 Hz, rispettivamente. Disegni di M. M. che riproducono alcune immagini realizzate da C. Hutchins con il metodo dell’interferogramma laser (7).
Ricostruire un legame indebolito ma mai spezzato
Quale potrebbe essere la vera causa del distacco fra il mondo artistico e il mondo scientifico, e perché tale distacco viene oggi considerato un problema? In fondo si potrebbe accettare l’ipotesi che il naturale sviluppo delle discipline scientifiche conduca necessariamente alla specializzazione e quindi a un allontanamento perfino tra discipline affini. Se oggi un matematico e un astrofisico hanno difficoltà a raccontarsi l’un l’altro le proprie ricerche più avanzate, perché stupirsi che ciò accada tra la scienza e l’arte? Eppure, gli esempi presentati in precedenza, seppure limitati alla musica, mostrano quanto sia ancora vivo questo legame.
È probabile che il problema risieda nella percezione sociale di queste discipline. Ne soffrono un po’ in tutto il mondo, in particolare, le discipline scientifiche. Tanti studenti, sin dai primi anni della scuola secondaria, si allontanano dallo studio della scienza perché percepita come troppo difficile, fredda, utilitaristica e slegata da altri aspetti come, per esempio, la bellezza. È ancora troppo basso il numero di studentesse che si iscrivono alle facoltà scientifiche malgrado i brillanti risultati conseguiti in queste materie nella scuola secondaria. Nonostante la notevole considerazione per le scienze, troppi studenti se ne allontanano precocemente, un fenomeno ancora più evidente in categorie sociali a rischio.
È anche per questi motivi che continua a farsi strada l’idea di affiancare all’insegnamento delle discipline STEM (Science, Technology, Engineering, Mathematics) l’insegnamento delle arti. Si comincia a parlare sempre più di STEAM, ritenendo necessario l’inserimento della “A” di Arte per modificare la percezione delle discipline scientifiche e renderle più inclusive.
Le stesse osservazioni valgono in modo speculare. In un’intervista concessa alla televisione svizzera negli anni ‘70, il grande scrittore Gianni Rodari, alla domanda: “Cosa si deve fare per diventare scrittori?”, risponde in modo apparentemente provocatorio, in realtà lungimirante: “Studiare matematica”[8].
Sarebbe il caso di trarre spunto dalla tradizione greca per individuare e valorizzare ciò che può apparire un paradosso: gli aspetti scientifici dell’arte e gli aspetti artistici della scienza.
E chissà se i violinisti nascosti nelle scene romantiche dei film non aggiungano alla chimica dei momenti sentimentali... un po’ di matematica.
Note
1) Andrea Frova. 2008. Fisica nella Musica. Bologna: Zanichelli.
2) Tartini ed Eulero: http://www.discovertartini.eu/archives
3) G. Mazzola, M. Mannone e Y. Pang, 2016. Cool Math for Hot Music. Heidelberg: Springer.
4) S. Tunnicliffe. (2000). “Wolfgang Graeser (1906-28): A Forgotten Genius”. The Musical Times, 141(1870), 42-44
6) R. J. Stroeker. 2015. “On the Shape of a Violin”. Mathematics Magazine, 88(4), 247-259, https://www.tandfonline.com/doi/abs/10.4169/math.mag.88.4.247
7) C. Hutchins, “L’acustica dei piani armonici di violino”, Le Scienze, 1981, n.160, pp. 86-99. http://download.kataweb.it/mediaweb/pdf/espresso/scienze/1981_160_6.pdf .
8) Gianni Rodari, intervista: https://www.rsi.ch/play/tv/decadi-anni-70/video/i-bambini-intervistano-gianni-rodari?id...
