Roger Barlow è un fisico dell’Università di Manchester, autore di un autorevole e serio manuale di statistica per fisici, intitolato con poca fantasia Statistica – Guida all’uso dei metodi statistici nelle scienze fisiche. A pag. 27, dopo un complicato esempio basato sull’efficienza dei rivelatori di raggi cosmici, cambia sorprendentemente argomento:
In un esperimento sulla percezione extrasensoriale, un soggetto deve indovinare il simbolo su una carta. Ci sono cinque differenti simboli, quindi ha una probabilità del 20% di indovinare per caso. Se si fanno sei prove, qual è la probabilità di azzeccarne per caso più di metà?
Sta evidentemente parlando di un esperimento con le carte Zener, spesso usate in parapsicologia, che riportano cinque simboli molto semplici (cerchio, croce, onde, quadrato, stella). La ragione di quell’esempio, apparentemente fuori contesto, è che molti degli esperimenti per verificare presunti fenomeni misteriosi appartengono alla stessa categoria, quella degli esperimenti binomiali, di cui sono diventati casi classici. Vediamone un paio di altri esempi.
Non molti anni fa si presentò al CICAP un anziano signore. Aveva notato uno strano fenomeno: tenendo un pendolino sospeso su una fotografia, questo si comportava in modo molto diverso se la persona raffigurata nella foto era viva oppure morta. Nel primo caso cominciava a ruotare vivacemente, mentre nel secondo rimaneva verticale e quasi fermo.
La spiegazione poteva essere semplice. Un pendolino è un amplificatore meccanico: a movimenti della mano anche molto piccoli possono corrispondere ampie oscillazioni del pendolino. Dato che, come raccontò, aveva sempre provato con fotografie di persone che conosceva, era in effetti possibile che si trattasse del fenomeno noto come azione ideomotoria. Quando sapeva che la persona nella foto era viva, si aspettava che il pendolino oscillasse e, con piccoli movimenti involontari della mano, faceva succedere proprio questo. Un semplice esperimento basato su un protocollo cieco simile a quello descritto nel numero 2 di Query, avrebbe impedito che le sue aspettative influenzassero il risultato. Per cui selezionammo una quarantina di fotografie raffiguranti venti persone al momento ancora vive e venti morti, tutti sconosciuti senza alcuna relazione con il signore del pendolino: tirando a indovinare ne avrebbe indovinati circa la metà. Se ne avesse azzeccati molti di più avremo avuto davanti un genuino fenomeno paranormale, altrimenti l’azione ideomotoria sarebbe stata la spiegazione più plausibile.
Un ulteriore esempio è il classico matching test usato per verificare le affermazioni degli astrologi. A un astrologo è fornito un profilo psicologico di un soggetto, i dati di nascita del soggetto stesso e di altre due persone prese a caso. Deve a questo punto cercare di capire, usando le informazioni che sarebbero contenute nei dati di nascita, a quale dei soggetti corrisponda il profilo. Se si ripete più volte l’esperimento, naturalmente con soggetti diversi, un astrologo che tiri a indovinare (ossia che non abbia alcuna informazione di carattere “astrologico”) indovinerebbe in media una volta su tre.
Proviamo a individuare che cosa hanno in comune i tre casi:
Sono queste quattro caratteristiche a individuare la categoria di esperimenti noti come esperimenti binomiali: in tutti questi casi la legge statistica che descrive la probabilità di successo nelle prove ripetute è la distribuzione binomiale. Vediamo di cosa si tratta e, soprattutto, a cosa serve.
Tirare a indovinare se la persona nella foto è viva o morta è come lanciare una moneta e cercare di indovinare se verrà testa o croce: indovinerò circa in metà dei casi. Però non è detto che indovini esattamente metà delle volte. Ripetendo più volte l’esperimento, ci saranno casi in cui indovinerò proprio venti volte (la metà delle quaranta fotografie), ma altri in cui indovinerò qualche volta in più o in meno. Quante volte deve scegliere correttamente “vivo” o “morto” per poter essere sicuri che si tratti di un genuino fenomeno paranormale, e non di un radioestesista particolarmente fortunato?
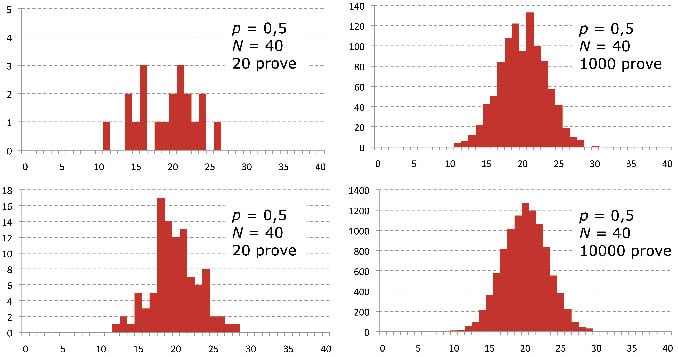
Facciamo il semplice esperimento che si trova su tutti i manuali di statistica, compreso quello di Barlow: proviamo a indovinare vivi e morti (oppure il risultato del lancio di una moneta), annotiamo quante volte indoviniamo e ripetiamo l’operazione più volte. Poi prepariamo un istogramma: disegniamo un grafico con una colonna per ogni possibile risultato (non ho indovinato neanche una volta, ho indovinato una volta sola, due volte, tre volte, eccetera fino a quaranta) in cui l’altezza di ciascuna colonna rappresenta quante volte ho ottenuto quel particolare risultato. Dopo venti esperimenti (sono ottocento lanci di moneta, ma non c’è bisogno di farli davvero: io ho fatto simulare l’esperimento al computer) il grafico ottenuto sarà simile a quello in figura 1. È bruttino, ma migliora subito se invece di venti esperimenti ne facciamo 100. Si nota immediatamente una cosa: il grafico ha una caratteristica forma a campana, con un “picco” centrale e due “code” che si allargano ai lati. Il picco è centrato più o meno in corrispondenza del valore che ci aspettavamo “in media”, cioè venti. Se continuiamo a lanciare le monete la forma del grafico rimane più o meno la stessa, diventando più regolare e simmetrico, ben centrato intorno al valore atteso. Facendo moltissime prove il grafico riprodurrà quello della distribuzione binomiale, sovrapposto in blu. Di solito, naturalmente, non c’è bisogno di rifare migliaia di volte la prova: se l’esperimento ha le quattro caratteristiche descritte prima, sappiamo già che avrà una distribuzione binomiale e potrò fare direttamente i calcoli (la formula si trova in qualunque manuale di statistica e, per esempio, il popolare foglio di calcolo Microsoft Excel include una funzione per calcolarla). Basterà sapere il numero N di prove e la probabilità p di successo di una singola prova: nei tre esempi descritti all’inizio, p vale 0.2 (uno su cinque) per l’esperimento con le carte Zener, 0.5 (uno su due) per il test del radioestesista e 0.33 (uno su tre) per il matching test dell’astrologo. Come si usa il grafico della figura 1?
L’istogramma che abbiamo disegnato è la distribuzione di frequenza del fenomeno; l’altezza di ciascuna colonna indica la probabilità che, facendo un ulteriore esperimento, il risultato vada a finire proprio lì. Come ci potevamo aspettare, le colonne più alte sono quelle vicino al picco, mentre è molto meno probabile indovinare per esempio trentacinque volte su quaranta, indice che in questo caso il risultato probabilmente non è dovuto alla fortuna. Per calcolare, per esempio, quanta probabilità c’è di indovinare più di 25 volte basta sommare l’altezza delle colonne dalla numero 26 in poi, ottenendo (fidatevi) 40 su 1000, cioè il 4%. Di solito, però, si procede al contrario: quello che serve calcolare è quante volte deve indovinare il veggente per essere sicuri che il risultato non sia dovuto alla sua fortuna. Essere completamente sicuri non si può, però si può decidere di essere sicuri al 99%, al 99.9%, o quello che si vuole (ne abbiamo parlato sul numero 4 di Query). In questo caso, l’operazione da fare sul nostro grafico è cominciare a sommare l’altezza delle colonne, a partire da sinistra, fino a che il numero che abbiamo ottenuto sia (per esempio) il 99% di tutti i casi: la colonna a cui saremo arrivati sarà quella corrispondente al numero di successi che il veggente dovrà ottenere: se usiamo il grafico in figura, otteniamo 27. Per cui, se il veggente indovinerà più di 27 volte su 40 sapremo che, con una probabilità del 99%, l’impresa non è dovuta al caso. Se vorremo essere sicuri al 99.9%, ce ne vorranno invece 29.
In un esperimento sulla percezione extrasensoriale, un soggetto deve indovinare il simbolo su una carta. Ci sono cinque differenti simboli, quindi ha una probabilità del 20% di indovinare per caso. Se si fanno sei prove, qual è la probabilità di azzeccarne per caso più di metà?
Sta evidentemente parlando di un esperimento con le carte Zener, spesso usate in parapsicologia, che riportano cinque simboli molto semplici (cerchio, croce, onde, quadrato, stella). La ragione di quell’esempio, apparentemente fuori contesto, è che molti degli esperimenti per verificare presunti fenomeni misteriosi appartengono alla stessa categoria, quella degli esperimenti binomiali, di cui sono diventati casi classici. Vediamone un paio di altri esempi.
Non molti anni fa si presentò al CICAP un anziano signore. Aveva notato uno strano fenomeno: tenendo un pendolino sospeso su una fotografia, questo si comportava in modo molto diverso se la persona raffigurata nella foto era viva oppure morta. Nel primo caso cominciava a ruotare vivacemente, mentre nel secondo rimaneva verticale e quasi fermo.
La spiegazione poteva essere semplice. Un pendolino è un amplificatore meccanico: a movimenti della mano anche molto piccoli possono corrispondere ampie oscillazioni del pendolino. Dato che, come raccontò, aveva sempre provato con fotografie di persone che conosceva, era in effetti possibile che si trattasse del fenomeno noto come azione ideomotoria. Quando sapeva che la persona nella foto era viva, si aspettava che il pendolino oscillasse e, con piccoli movimenti involontari della mano, faceva succedere proprio questo. Un semplice esperimento basato su un protocollo cieco simile a quello descritto nel numero 2 di Query, avrebbe impedito che le sue aspettative influenzassero il risultato. Per cui selezionammo una quarantina di fotografie raffiguranti venti persone al momento ancora vive e venti morti, tutti sconosciuti senza alcuna relazione con il signore del pendolino: tirando a indovinare ne avrebbe indovinati circa la metà. Se ne avesse azzeccati molti di più avremo avuto davanti un genuino fenomeno paranormale, altrimenti l’azione ideomotoria sarebbe stata la spiegazione più plausibile.
Un ulteriore esempio è il classico matching test usato per verificare le affermazioni degli astrologi. A un astrologo è fornito un profilo psicologico di un soggetto, i dati di nascita del soggetto stesso e di altre due persone prese a caso. Deve a questo punto cercare di capire, usando le informazioni che sarebbero contenute nei dati di nascita, a quale dei soggetti corrisponda il profilo. Se si ripete più volte l’esperimento, naturalmente con soggetti diversi, un astrologo che tiri a indovinare (ossia che non abbia alcuna informazione di carattere “astrologico”) indovinerebbe in media una volta su tre.
Proviamo a individuare che cosa hanno in comune i tre casi:
- l’esperimento implica prove ripetute (o su più soggetti simili tra loro, come nel secondo e terzo caso);
- ogni singola prova può avere solo due risultati: successo o fallimento, indovinato o sbagliato;
- la probabilità di successo è costante (cioè è sempre la stessa in ognuna delle prove);
- le prove sono indipendenti tra loro (cioè il risultato di una prova non influenza le successive).
Sono queste quattro caratteristiche a individuare la categoria di esperimenti noti come esperimenti binomiali: in tutti questi casi la legge statistica che descrive la probabilità di successo nelle prove ripetute è la distribuzione binomiale. Vediamo di cosa si tratta e, soprattutto, a cosa serve.
Tirare a indovinare se la persona nella foto è viva o morta è come lanciare una moneta e cercare di indovinare se verrà testa o croce: indovinerò circa in metà dei casi. Però non è detto che indovini esattamente metà delle volte. Ripetendo più volte l’esperimento, ci saranno casi in cui indovinerò proprio venti volte (la metà delle quaranta fotografie), ma altri in cui indovinerò qualche volta in più o in meno. Quante volte deve scegliere correttamente “vivo” o “morto” per poter essere sicuri che si tratti di un genuino fenomeno paranormale, e non di un radioestesista particolarmente fortunato?
Facciamo il semplice esperimento che si trova su tutti i manuali di statistica, compreso quello di Barlow: proviamo a indovinare vivi e morti (oppure il risultato del lancio di una moneta), annotiamo quante volte indoviniamo e ripetiamo l’operazione più volte. Poi prepariamo un istogramma: disegniamo un grafico con una colonna per ogni possibile risultato (non ho indovinato neanche una volta, ho indovinato una volta sola, due volte, tre volte, eccetera fino a quaranta) in cui l’altezza di ciascuna colonna rappresenta quante volte ho ottenuto quel particolare risultato. Dopo venti esperimenti (sono ottocento lanci di moneta, ma non c’è bisogno di farli davvero: io ho fatto simulare l’esperimento al computer) il grafico ottenuto sarà simile a quello in figura 1. È bruttino, ma migliora subito se invece di venti esperimenti ne facciamo 100. Si nota immediatamente una cosa: il grafico ha una caratteristica forma a campana, con un “picco” centrale e due “code” che si allargano ai lati. Il picco è centrato più o meno in corrispondenza del valore che ci aspettavamo “in media”, cioè venti. Se continuiamo a lanciare le monete la forma del grafico rimane più o meno la stessa, diventando più regolare e simmetrico, ben centrato intorno al valore atteso. Facendo moltissime prove il grafico riprodurrà quello della distribuzione binomiale, sovrapposto in blu. Di solito, naturalmente, non c’è bisogno di rifare migliaia di volte la prova: se l’esperimento ha le quattro caratteristiche descritte prima, sappiamo già che avrà una distribuzione binomiale e potrò fare direttamente i calcoli (la formula si trova in qualunque manuale di statistica e, per esempio, il popolare foglio di calcolo Microsoft Excel include una funzione per calcolarla). Basterà sapere il numero N di prove e la probabilità p di successo di una singola prova: nei tre esempi descritti all’inizio, p vale 0.2 (uno su cinque) per l’esperimento con le carte Zener, 0.5 (uno su due) per il test del radioestesista e 0.33 (uno su tre) per il matching test dell’astrologo. Come si usa il grafico della figura 1?
